den nedenfor nevnte artikkelen gir et nært syn På Cobb-Douglas Produksjonsfunksjon. cobb-Douglas produksjonsfunksjonen er basert på den empiriske studien Av Den Amerikanske produksjonsindustrien laget av Paul H. Douglas og C. W. Cobb. Det er en lineær homogen produksjonsfunksjon av grad en som tar hensyn til to innganger, arbeidskraft og kapital, for hele produksjonen av den .industri.

Cobb-Douglas produksjonsfunksjonen uttrykkes som:

Q = Ala Cß

Hvor Q er utgang og L og С er innganger av henholdsvis arbeidskraft og kapital. A, a og β er positive parametere der = a > o, β > o.

ligningen forteller at utgangen avhenger direkte Av L Og C, og den delen av utgangen som ikke kan forklares Med L og С forklares Av A som er «gjenværende», ofte kalt teknisk endring.

produksjonsfunksjonen løst Av Cobb-Douglas hadde 1/4 kapitalbidrag til økningen i industrien og 3/4 av arbeidskraft, slik at C-d produksjonsfunksjonen er

Q = AL3/4 C1/4

som viser konstant avkastning i skala fordi summen av verdiene Av L og С er lik en: (3/4 + 1/4), dvs. (A + β = 1). Arbeidskoeffisienten i C-d-funksjonen måler den prosentvise økningen i (Q som ville følge av en 1 prosent økning I L, mens Den Holdt С som konstant.

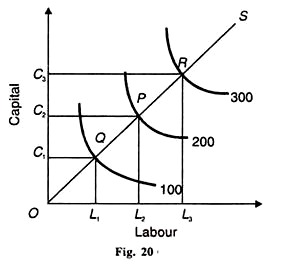
Tilsvarende Er В den prosentvise økningen I Q som ville følge av en 1 prosent økning I C, mens du holder L som konstant. Cd – produksjonsfunksjonen som viser konstant retur til skala er avbildet I Figur 20. Arbeidsinnsats er tatt på den horisontale aksen og kapital på den vertikale aksen.

for å produsere 100 enheter av produksjon, BENYTTES ОС, kapitalenheter og ol-enheter av arbeidskraft. Hvis produksjonen skulle dobles til 200, må innsatsfaktorene for arbeidskraft og kapital dobles. ОС ER nøyaktig det dobbelte av ос1 OG AV ol2 ER DET DOBBELTE av ol2.

Tilsvarende, Hvis produksjonen skal økes tre ganger til 300, må arbeids-og kapitalenhetene økes tre ganger. OC3 OG OL3 er tre ganger større enn ОС 1, og ol1, henholdsvis. EN annen metode er å ta skalalinjen eller ekspansjonsbanen som forbinder likevektspunktene Q, P og R. OS er skalalinjen eller ekspansjonsbanen som går sammen med disse punktene.

det viser at isokvantene 100, 200 og 300 er like langt unna. DERMED, PÅ OS skala linjen OQ = QP = PR som viser at når kapital OG arbeidskraft økes i like proporsjoner, produksjonen øker også i samme andel.

Kritikk Av C-D Produksjon Funksjon:

C-D produksjon funksjon har blitt kritisert Av Arrow, Chenery, Minhas Og Solow som omtalt nedenfor:

1. C – d-produksjonsfunksjonen vurderer bare to innganger, arbeidskraft og kapital, og forsømmer noen viktige innganger, som råvarer, som brukes i produksjonen. Det er derfor ikke mulig å generalisere denne funksjonen til mer enn to innganger.

2. I Cd-produksjonsfunksjonen oppstår problemet med måling av kapital fordi det bare tar mengden kapital som er tilgjengelig for produksjon. Men full bruk av tilgjengelig kapital kan kun gjøres i perioder med full sysselsetting. Dette er urealistisk fordi ingen økonomi alltid er fullt ansatt.

3. C – d-produksjonsfunksjonen kritiseres fordi den viser konstant retur til skala. Men konstant avkastning til skala er ikke en realitet, for enten økende eller avtagende avkastning til skala gjelder for produksjonen.

det er ikke mulig å endre alle innganger for å få en forholdsmessig endring i utgangene til alle bransjer. Noen innganger er knappe og kan ikke økes i samme forhold som rikelig innganger. På den annen side, innganger som maskiner, entreprenørskap, etc. de er udelelige. Når produksjonen øker på grunn av bruk av udelelige faktorer til maksimal kapasitet, faller per enhetskostnad.

når tilførselen av innganger er knappe og udelbarhet er tilstede, er det ikke mulig å returnere konstant til skala. Når enhetene av forskjellige innganger økes i produksjonsprosessen, fører stordriftsfordeler og spesialisering til økende avkastning i skala.

i praksis vil ingen entreprenør imidlertid øke de ulike enhetene av innganger for å få en forholdsmessig økning i produksjonen. Hans bestrebelse er å ha mer enn forholdsmessig økning i produksjonen, men avtagende avkastning i skala er heller ikke utelukket.

4. C – d-produksjonsfunksjonen er basert på antagelsen om substituerbarhet av faktorer og forsømmer komplementariteten til faktorer.

5. Denne funksjonen er basert på antagelsen om perfekt konkurranse i faktormarkedet som er urealistisk. Dersom denne antakelsen imidlertid faller, representerer ikke koeffisientene α og β faktorandeler.

6. En av svakhetene Ved C – d-funksjonen er aggregeringsproblemet. Dette problemet oppstår når denne funksjonen brukes på alle firmaer i en bransje og til hele bransjen. I denne situasjonen vil det være mange produksjonsfunksjoner med lav eller høy aggregering. Dermed Måler C – d-funksjonen ikke hva den tar sikte på å måle.

Konklusjon:

dermed er gjennomførbarheten Av Cd-produksjonsfunksjonen i produksjonsindustrien et tvilsomt forslag. Dette gjelder ikke for jordbruk der for intensiv dyrking, øker mengden av innganger ikke vil øke produksjonen proporsjonalt. Selv da kan det ikke nektes at konstant retur til skala er et stadium i livet til et firma, industri eller økonomi. Det er en annen ting at dette stadiet kan komme etter en tid og for en kort stund.

Det Er Viktig:

Til tross for denne kritikken er C – d-funksjonen av stor betydning.

1. Det har blitt brukt mye i empiriske studier av produksjonsindustrier og i interindustrielle sammenligninger.

2. Det brukes til å bestemme de relative andelene av arbeidskraft og kapital i total produksjon.

3. Det brukes til å bevise Eulers Teorem.

4. Parametrene a og b representerer elastisitetskoeffisienter som brukes til intersektorielle sammenligninger.

5. Denne produksjonsfunksjonen er lineær homogen av grad en som viser konstante avkastninger I skala, hvis α + β = 1, er det økende avkastninger i skala og hvis α + β < 1, er det avtagende avkastninger i skala.

6. Økonomer har utvidet denne produksjonsfunksjonen til mer enn to variabler.