en tensor er en matrise av data (tall, funksjoner, etc.) som er utvidet i et hvilket som helst tall (0 og større) av dimensjoner. Antall dimensjoner kalles rang av tensor.

Rang 0 tensor

en tensor som ikke har noen dimensjoner (0).

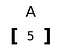
A er en 0 dimensjonal tensor

rang 1 tensor

en tensor som er utvidet i bare en dimensjon.

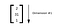
Rank 2 tensor

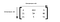
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

Skalar

en skalar er 0 rang tensor. I fysikk er ulike mengder representert som en skalar som: Avstand (500 km), Temperatur (10º), Hastighet (34 km/t), etc.

Vektor

en rang 1 tensor kalles en vektor. Fysiske mengder Som Hastighet (10 m / s), Forskyvning (54 m Mot Øst), Elektromagnetisk Felt (1 V/m).

Forskjell mellom skalar og vektor :

en mengde som ikke krever tilleggsinformasjon (for eksempel retning) med den (som temperatur) er representert som skalar. Mens en mengde som trenger retning som skal spesifiseres sammen med størrelsen, er representert med en vektor (som elektrisk felt).

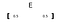
E Er en vektor eller en rang 1 tensor

en vektor er betegnet med fet bokstav (som»e») eller en pil over bokstaven.

for å plotte en vektor bruker vi elementene som verdien av koordinater (henholdsvis x, y og z-aksen). Her blir første element (0,5) tatt som x-verdi og andre element (også 0,5) tatt som y-verdi (hvis vi hadde tre elementer, ville den tredje ha vært z-verdi).

Vektor e plottet på grafen som en blå prikk / figcaption>

etter å plotte vektoren som et punkt legger vi en pil til den, fra opprinnelse(0,0).

en vektor er ganske enkelt en matrise som har enten en rad (kalt kolonnevektor) eller en kolonne (kalt radvektor).

Matrise

en matrise er en rang 2 tensor. Vi har sett på matrix tidligere.

en tensor med rang større enn 2 kalles ganske enkelt «tensor» (det er ikke noe spesifikt navn for tensorer med rang mer enn 2).Begrepet tensor generaliserer matriser, vektorer og skalarer under ett tak (de er alle tensorer, men med forskjellige ranger).

Matriser som produkt av vektorer:

når to vektorer multipliseres, danner de en matrise.

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Dermed kan noen matriser brytes ned som et produkt av to vektorer.