Regresjonsanalyse > Homoscedasticitet / Homogenitet Av Varians / Antagelse Av Lik Varians

bilde: sreebot| wikimedia commons

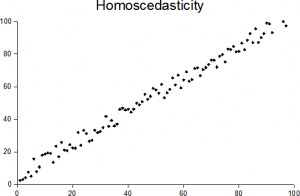
Enkelt sagt Betyr Homoscedasticity «å ha samme scatter.»For at det skal eksistere i et sett med data, må punktene være omtrent samme avstand fra linjen,som vist på bildet ovenfor. Det motsatte er heteroscedasticitet («forskjellig scatter»), hvor poeng er i vidt varierende avstander fra regresjonslinjen.

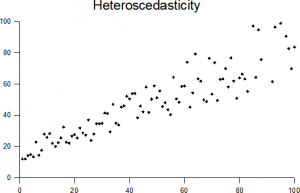
punktene høyere på x-aksen har en større varians enn mindre verdier.

Merk at jeg sa» avstand » her og ikke varians. Når du ser på en graf, er det lettere å se på avstandene fra punktene til linjen for å avgjøre om et sett med data viser homoscedasticitet. Teknisk sett er det variansen som teller, og det er det du vil bruke i beregninger. Men som varians krever en formel, er det umulig å øyeboll på en graf.

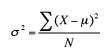
Varians formel.

som varians er bare standardavviket kvadrert, kan du også se homoscedasticity beskrevet som en tilstand der standardavvikene er like for alle punkter.

i mer formelle termer

du kommer sjelden til å komme over et sett med data som har en varians på null. Du er mer sannsynlig å se avvik fra alt fra 0,01 til 101,01. Så når er et datasett klassifisert som å ha homoscedasticity? Den generelle tommelfingerregelen1 er:

hvis forholdet mellom den største variansen og den minste variansen er 1,5 eller under, er dataene homoskedastiske.

Hva Er Forutsetningen Om Lik Varians?

antagelsen om like avvik (dvs.antagelse om homoskedastisitet) antar at forskjellige prøver har samme varians, selv om de kom fra forskjellige populasjoner. Forutsetningen er funnet i mange statistiske tester, inkludert Analyse Av Varians (ANOVA) Og Studentens T-Test. Andre tester, som Welchs T-Test, krever ikke like avvik i det hele tatt.Å kjøre en test uten å sjekke for like avvik kan ha en betydelig innvirkning på resultatene dine og kan til og med ugyldiggjøre dem helt. Hvor mye resultatene dine påvirkes, avhenger av hvilken test du bruker og hvor følsom testen er for ulik avvik. For eksempel, mens en anova-test med fast faktor med like utvalgsstørrelser bare påvirkes et lite beløp, kan EN ANOVA med ulik utvalgsstørrelse gi deg helt ugyldige resultater.

forutsetningen om like avvik brukes også i lineær regresjon, som antar at data er homoskedastiske. Enkelt sagt, hvis dataene dine er bredt spredt om (som å kegleform i det heteroscedastiske bildet ovenfor), vil regresjon ikke fungere så bra. For mer om dette emnet, se Forutsetninger & Betingelser For Regresjon.

Testing for Homogenitet Av Varians

Tester som du kan kjøre for å sjekke at dataene dine oppfyller denne antagelsen, inkluderer:

• Bartlett ‘S Test
• Box’ S M Test
• Brown-Forsythe Test
• Hartleys Fmax test
• Levenes Test

——————————————————————————

Trenger du hjelp med lekser eller test spørsmål? Med Chegg Study kan du få trinnvise løsninger på dine spørsmål fra en ekspert på feltet. Din første 30 minutter med En Chegg veileder er gratis!