het onderstaande artikel geeft een goed beeld van de Cobb-Douglas productiefunctie. de productiefunctie van Cobb-Douglas is gebaseerd op de empirische studie van de Amerikaanse industrie van Paul H. Douglas en C. W. Cobb. Het is een lineaire homogene productiefunctie van graad één die rekening houdt met twee inputs, arbeid en kapitaal, voor de gehele output van de .industrie.

De Cobb-Douglas productiefunctie wordt uitgedrukt als:

Q = ALa Cß

waarin Q Is output en L en С zijn input van Arbeid en kapitaal. A, a en β zijn positieve parameters waarbij=a > O, β > O.

de vergelijking vertelt dat de output direct afhankelijk is van L en C, en dat deel van de output dat niet kan worden verklaard door L en С wordt verklaard door A dat het ‘restant’ is, vaak technische verandering genoemd.

de door Cobb-Douglas opgeloste productiefunctie had 1/4 inbreng van kapitaal in de toename van de verwerkende industrie en 3/4 van de arbeid, zodat de C-D productiefunctie

Q = AL3/4 C1/4

die een constant rendement op schaal geeft omdat het totaal van de waarden van L en С gelijk is aan 1: (3/4 + 1/4), d.w.z.(A + β = 1) . De coëfficiënt van de arbeider in de C-D functie meet de procentuele toename in (Q die zou voortvloeien uit een 1 procent toename in L, terwijl С constant wordt gehouden.

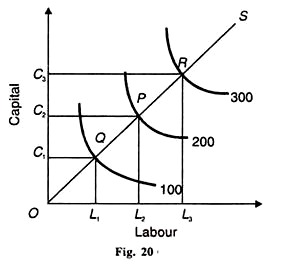
evenzo is В de procentuele stijging van Q die het gevolg zou zijn van een stijging van 1% In C, terwijl L constant blijft. De C-D-productiefunctie die een constant rendement op schaal geeft, is afgebeeld in figuur 20. Arbeidsinput wordt genomen op de horizontale as en kapitaal op de verticale as.

om 100 eenheden output te produceren, worden oс, eenheden kapitaal en OL arbeidseenheden gebruikt. Als de productie zou worden verdubbeld tot 200, zouden de input van Arbeid en kapitaal moeten worden verdubbeld. ОС is precies dubbel van ОС1 en van OL2 is dubbel van OL2.

om de output driemaal te verhogen tot 300, moeten de eenheden arbeid en kapitaal driemaal worden verhoogd. OC3 en OL3 zijn drie keer groter dan respectievelijk ОС1 en OL1. Een andere methode is om de schaallijn of uitbreidingspad te nemen die de evenwichtspunten verbindt Q, P en R. OS is de schaallijn of uitbreidingspad die deze punten verbindt.

Het toont aan dat de isoquanten 100, 200 en 300 op gelijke afstand staan. Dus op de OS schaal lijn OQ = QP = PR, waaruit blijkt dat wanneer kapitaal en arbeid in gelijke verhoudingen worden verhoogd, de output ook in dezelfde verhouding toeneemt.

kritiek op C-D productiefunctie:

De C-D productiefunctie is bekritiseerd door Arrow, Chenery, Minhas en Solow zoals hieronder besproken:

1. De C-D-productiefunctie houdt slechts rekening met twee inputs, arbeid en kapitaal, en verwaarloost enkele belangrijke inputs, zoals grondstoffen, die in de productie worden gebruikt. Het is daarom niet mogelijk deze functie te veralgemenen tot meer dan twee ingangen.

2. In de C-D-productiefunctie ontstaat het probleem van de meting van het kapitaal, omdat het slechts de hoeveelheid kapitaal nodig heeft die voor de productie beschikbaar is. Maar het beschikbare kapitaal kan alleen volledig worden benut in perioden van volledige werkgelegenheid. Dit is onrealistisch omdat geen enkele economie altijd volledig werkzaam is.

3. De C-D-productiefunctie wordt bekritiseerd omdat deze constant terugkeert naar Schaal. Maar een constante schaalopbrengst is geen werkelijkheid, want zowel een toenemende als een afnemende schaalopbrengst is van toepassing op de productie.

het is niet mogelijk om alle inputs te veranderen om een evenredige verandering in de output van alle industrieën tot stand te brengen. Sommige inputs zijn schaars en kunnen niet in dezelfde mate worden verhoogd als overvloedige inputs. Aan de andere kant, inputs zoals machines, ondernemerschap, enz. ondeelbaar zijn. Naarmate de productie toeneemt als gevolg van het gebruik van ondeelbare factoren voor hun maximale capaciteit, dalen de kosten per eenheid.

wanneer het aanbod van inputs schaars is en er verschillen zijn, is een constant rendement op schaal niet mogelijk. Wanneer de eenheden van verschillende inputs in het productieproces worden verhoogd, leiden schaalvoordelen en specialisatie tot een hoger rendement op schaal.

in de praktijk zal echter geen enkele ondernemer de verschillende productie-eenheden willen verhogen om een evenredige toename van de productie te bewerkstelligen. Hij streeft naar een meer dan evenredige toename van de produktie, hoewel ook een kleiner rendement op schaal niet wordt uitgesloten.

4. De C-D productiefunctie is gebaseerd op de aanname van substitueerbaarheid van factoren en verwaarloost de complementariteit van factoren.

5. Deze functie is gebaseerd op de veronderstelling van perfecte concurrentie op de factormarkt, die onrealistisch is. Indien deze aanname echter wordt ingetrokken, geven de coëfficiënten α En β Geen factoraandelen weer.

6. Een van de zwakke punten van de C-D-functie is het aggregatieprobleem. Dit probleem doet zich voor wanneer deze functie wordt toegepast op elk bedrijf in een industrie en op de gehele industrie. In deze situatie zullen er veel productiefuncties van lage of hoge aggregatie zijn. De C-D-functie meet dus niet wat hij wil meten.

conclusie:

de uitvoerbaarheid van de C-D-productiefunctie in de verwerkende industrie is dus twijfelachtig. Dit geldt niet voor de landbouw, waar een verhoging van de productiemiddelen voor intensieve teelt de productie niet evenredig zal verhogen. Zelfs dan kan niet worden ontkend dat een constant rendement op schaal een fase is in het leven van een bedrijf, industrie of economie. Het is een ander ding dat deze fase kan komen na enige tijd en voor een korte tijd.

Het is belangrijk:

ondanks deze kritiek is de C-D functie van groot belang.

1. Het is op grote schaal gebruikt in empirische studies van de verwerkende industrie en in vergelijkingen tussen de industrie.

2. Het wordt gebruikt om het relatieve aandeel van Arbeid en kapitaal in de totale productie te bepalen.

3. Het wordt gebruikt om de Stelling van Euler te bewijzen.

4. De parameters a en b vertegenwoordigen elasticiteitscoëfficiënten die worden gebruikt voor intersectorale vergelijkingen.

5. Deze productiefunctie is lineair homogeen van graad 1, die een constante opbrengst naar schaal toont, Als α + β = 1, zijn er toenemende opbrengsten naar schaal en als α + β < 1, zijn er afnemende opbrengsten naar Schaal.

6. Economen hebben deze productiefunctie uitgebreid tot meer dan twee variabelen.