Functie-Notatie en het Evalueren van een Functie
De gemeenschappelijke notatie van een functie wordt meestal geschreven als
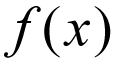
denk niet dat dit al te letterlijk, dat is f wordt vermenigvuldigd met x. In plaats daarvan, beschouw dit als een wiskundige uitdrukking die lezen als

OF

Functies kunnen ook worden op verschillende manieren geschreven met behulp van andere variabelen, zoals
- g(x), h(x) en k(x)
daarnaast functies kunnen nemen andere invoerwaarden dan x.
- f(a), h(r), en k(m)
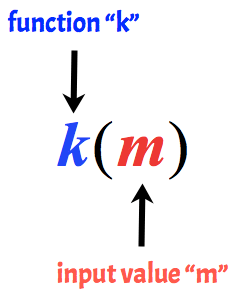
het belangrijkste idee is altijd om te onthouden dat de variabele buiten het haakje de “naam” van de functie is, terwijl de variabele binnen het haakje de invoerwaarde van de functie is.
het volgende wordt bijvoorbeeld functie k genoemd met een invoerwaarde van m.
basisvoorbeelden van het evalueren van functies
Voorbeeld 1: Evalueer de functie .
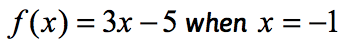
Dit is de normale notatie van functie waar de functie f is terwijl de invoerwaarde x is. om een functie te evalueren, willen we elke instantie van X in de uitdrukking en dan vereenvoudigen.
sinds x = – 1, vervangen we deze waarde in de functie en vereenvoudigen we. Zo krijgen we een oplossing die er zo uitziet.
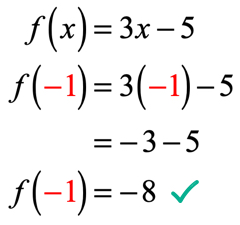
Voorbeeld 2: Evalueer de functie .
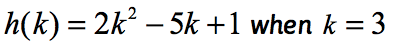
merk op dat de functie hier h is en de invoerwaarde k is. Net als in ons vorige voorbeeld willen we de numerieke waarde die aan k is toegewezen, vervangen door de gegeven functie en vereenvoudigen.
sinds k = 3 zou uw oplossing er ongeveer zo uit moeten zien
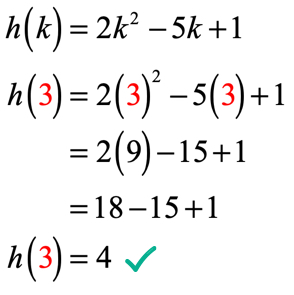
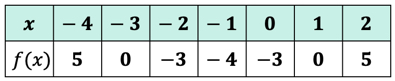
Voorbeeld 3: evalueer elke waarde van x in de onderstaande tabel met behulp van de onderstaande functie. Plot de punten in de xy-as en verbind de punten om de grafiek van de functie te onthullen.
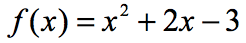

Aangezien er zeven x-ingangen, dat betekent dat we de functiewaarde zeven keer zo goed. Probeer dit zelf uit te werken en kom dan terug om je antwoorden te controleren.
Als u het goed hebt gedaan, zijn dit de waarden:
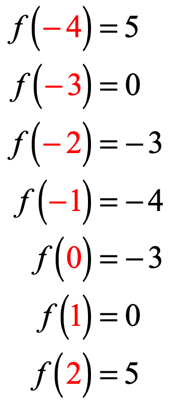
We kunnen nu deze uitvoerwaarden in de tabel plaatsen.
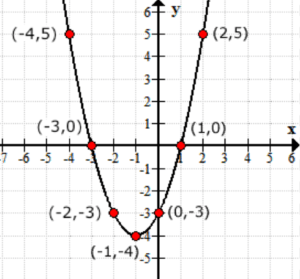
denk aan de uitvoerwaarden van de functie f\left( x \right) als de y-waarden. Zo ziet de grafiek eruit op de xy-as.
tussenliggende voorbeelden van het evalueren van functies
Voorbeeld 4: gegeven dat g\left( x \right) = {x^2} – 3x + 1, Zoek g\left( {2x – 1} \right).
in eerdere voorbeelden hebben we een functie geëvalueerd met een getal. Deze keer is de invoerwaarde niet langer een vaste numerieke waarde, maar in plaats daarvan een uitdrukking. Het lijkt misschien ingewikkeld, maar de procedure blijft hetzelfde.
We zullen elke instantie van x in g\left( x \right) vervangen door de invoerwaarde die 2x – 1 is. Vereenvoudig door het binomiaal te kwadrateren, de distributieve eigenschap toe te passen en soortgelijke termen te combineren.
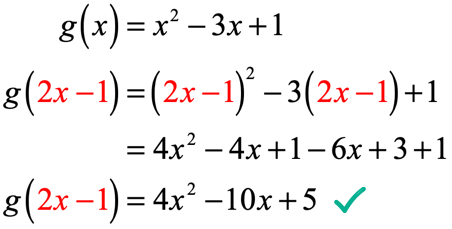
Voorbeeld 5: Gegeven is dat p\left( x \right) = {{4x – 1} \over x} , evalueren p\left( 1 \right) – p\left( { – 1} \right).
het probleem kan er in het begin intimiderend uitzien, maar zodra we het analyseren en toepassen wat we al weten over hoe we functies moeten evalueren, zou dit niet zo slecht moeten zijn!
wat we hier moeten doen is de functie Evalueren op x = 1 en vervolgens aftrekken met de waarde van de functie wanneer geëvalueerd op x = – \,1.
Wees zeer voorzichtig wanneer u de waarden vervangt en tijdens het vereenvoudigingsproces. Als je niet bij elke stap voorzichtig bent, is het heel gemakkelijk om fouten te maken wanneer je positieve en negatieve getallen optelt, aftrekt, vermenigvuldigt of deelt.
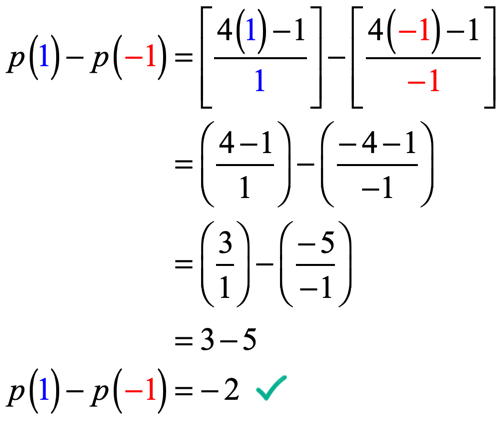
Advanced Voorbeeld van het Toepassen van het Concept van de Evaluatie van Functies
Voorbeeld 6: Als f\left( 2 \right) = 9, bereken de waarde van a in de functie hieronder.
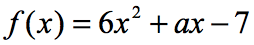
in de vergelijking, F \ left ( 2 \ right) = 9, wordt ons verteld dat als de input van de functie 2 is; de output van de functie zal 9 zijn. Aangezien de functie aan ons wordt gegeven, is onze eerste zet om ten minste de waarde van 2 te vervangen en dan te vereenvoudigen. Dit is wat we krijgen.
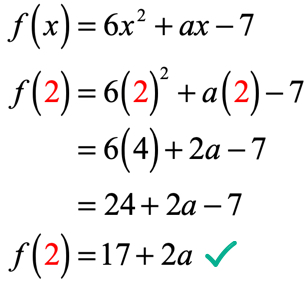
De uitvoer van de functie na evaluatie bij x = 2 is 17 + 2a. Vergeet niet, we worden ook verteld dat de uitgang 9 met behulp van de gegeven vergelijking f\left( 2 \right) = 9. Dus wat we nu moeten doen is stellen ze gelijk aan elkaar en los de lineaire vergelijking voor de onbekende waarde van een.
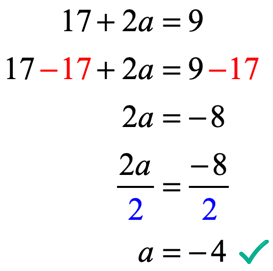
we controleren of de waarde van a = – \,4 in f(x) = 6{x^2} + ax – 7 kan de gegeven voorwaarde f\left( 2 \right) = 9 om een echt statement.

Het is waar! Daarom hebben we met succes opgelost voor de juiste waarde van a.
Leave a Reply