een alternatieve normaliteitstest is de Shapiro-Wilk test.

• Wat is een Kolmogorov-Smirnov normaliteitstest?
• SPSS Kolmogorov-Smirnov-test uit NPAR-TESTS
• SPSS Kolmogorov-Smirnov-test uit onderzoek variabelen
• rapportage van een Kolmogorov-Smirnov-Test
• verkeerde resultaten in SPSS?

Wat is een Kolmogorov-Smirnov normaliteitstest?

De Kolmogorov-Smirnov-test onderzoekt of scores
waarschijnlijk enige distributie volgen in een bepaalde populatie.Om verwarring te voorkomen zijn er 2 Kolmogorov-Smirnov-tests:

• Er is één monster Kolmogorov-Smirnov-test om te testen of een variabele een bepaalde verdeling in een populatie volgt. Deze ” gegeven verdeling “is meestal-niet altijd – de normale verdeling, vandaar”Kolmogorov-Smirnov normaliteitstest”.
• Er is ook de (veel minder voorkomende) onafhankelijke samples Kolmogorov-Smirnov test om te testen of een variabele identieke distributies heeft in 2 populaties.

in theorie kan” Kolmogorov-Smirnov-test ” verwijzen naar beide testen (maar verwijst meestal naar de Kolmogorov-Smirnov-test met één monster) en kan het beter worden vermeden. Trouwens, beide Kolmogorov-Smirnov tests zijn aanwezig in SPSS.

Kolmogorov – Smirnov Test-eenvoudig voorbeeld

stel dat ik een populatie van 1.000.000 mensen heb. Ik denk dat hun reactietijden bij een bepaalde taak normaal gesproken verdeeld zijn. Ik neem 233 van deze mensen en meet hun reactietijd.
nu zal de waargenomen frequentieverdeling van deze waarschijnlijk een beetje-maar niet te veel – verschillen van een normale verdeling. Dus ik doe een histogram over de waargenomen reactietijden en leg een normale verdeling over met dezelfde gemiddelde en standaardafwijking. Het resultaat wordt hieronder weergegeven.

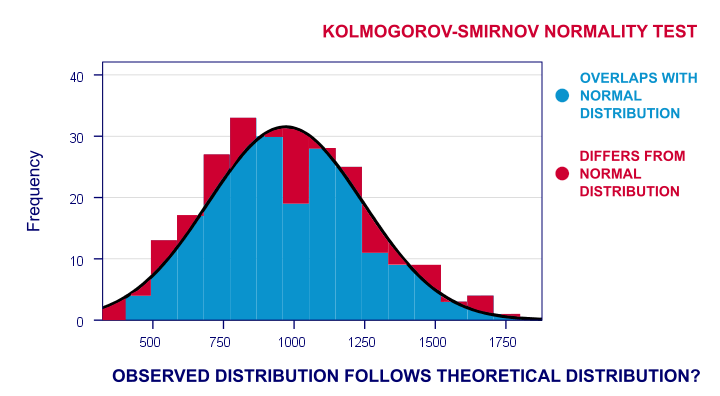
de frequentieverdeling van mijn scores overlapt niet geheel met mijn normale curve. Nu kan ik het percentage gevallen berekenen dat afwijkt van de normale curve-het percentage rode gebieden in de grafiek. Dit percentage is een teststatistiek: het drukt in een enkel getal uit hoeveel mijn gegevens verschillen van mijn nulhypothese. Het geeft dus aan in welke mate de waargenomen scores afwijken van een normale verdeling.
nu, als mijn nulhypothese waar is, dan zou dit deviatiepercentage waarschijnlijk vrij klein moeten zijn. Dat wil zeggen, een kleine afwijking heeft een hoge waarschijnlijkheidswaarde of p-waarde.omgekeerd is een enorm afwijkingspercentage zeer onwaarschijnlijk en suggereert dat mijn reactietijden niet een normale verdeling over de gehele populatie volgen. Een grote afwijking heeft dus een lage p-waarde. Als vuistregel, wereject de nulhypothese als p < 0.05.So als p < 0,05, geloven we niet dat onze variabele een normale verdeling in onze populatie volgt.

Kolmogorov – Smirnov Test-Test statistiek

dus dat is de makkelijkste manier om te begrijpen hoe de Kolmogorov-Smirnov normaliteitstest werkt. Rekenkundig werkt het echter anders: het vergelijkt de waargenomen versus de verwachte cumulatieve relatieve frequenties zoals hieronder weergegeven.

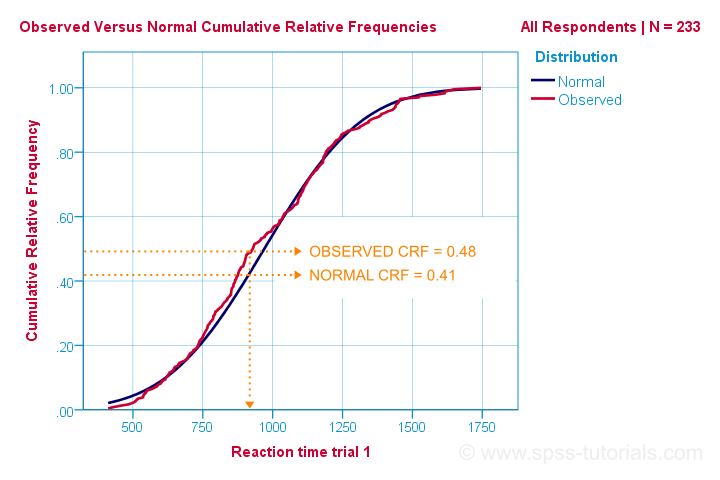
De Kolmogorov-Smirnov test gebruikt het maximale absolute verschil tussen deze curves als de teststatistiek aangegeven door D. in deze grafiek is het maximale absolute verschil D (0,48 – 0,41 =) 0,07 en het gebeurt bij een reactietijd van 960 milliseconden. Houd er rekening mee dat D = 0,07 als we zullen tegenkomen in onze SPSS-uitvoer in een minuut.

de Kolmogorov-Smirnov-test in SPSS

Er zijn 2 manieren om de test in SPSS uit te voeren:

• NPAR TESTS zoals gevonden onder analyseer Nonparametric Tests Legacy dialogen 1-Sample K-S… is onze methode van keuze, want het creëert mooi gedetailleerde output.
• onderzoek variabelen uit analyseren beschrijvende statistieken Explore is een alternatief. Dit commando voert zowel de Kolmogorov-Smirnov test als de Shapiro-Wilk normaliteit test uit.
  merk op dat EXAMINATE VARIABLES standaard listwise uitsluiting van ontbrekende waarden gebruikt. Dus als ik 5 variabelen test, gebruiken mijn 5 tests alleen gevallen die geen enkele Missing hebben op een van deze 5 variabelen. Dit is meestal niet wat je wilt, maar we zullen laten zien hoe je dit kunt vermijden.

We zullen beide methoden demonstreren met speedtasks.sav geheel, waarvan een deel Hieronder is weergegeven.

onze belangrijkste onderzoeksvraag is welke van de reactietijdvariabelen waarschijnlijk normaal wordt verdeeld in onze populatie?Deze gegevens zijn een schoolvoorbeeld van waarom u uw gegevens grondig moet inspecteren voordat u ze gaat bewerken of analyseren. Laten we dat doen en een aantal histogrammen uitvoeren van de syntaxis hieronder.

resultaat

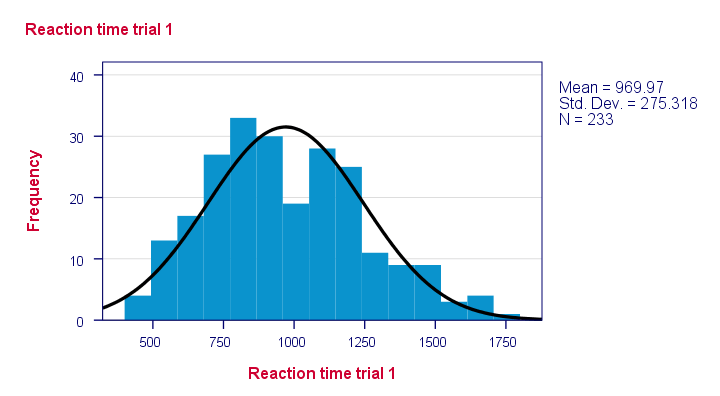
merk op dat sommige distributies er helemaal niet plausibel uitzien. Maar welke worden waarschijnlijk normaal verdeeld?

SPSS Kolmogorov-Smirnov-test van NPAR-TESTS

onze voorkeursoptie voor het uitvoeren van de Kolmogorov-Smirnov-test is onderanalyse niet-parametrische Tests Legacy dialogen 1-monster K-S… zoals hieronder getoond.

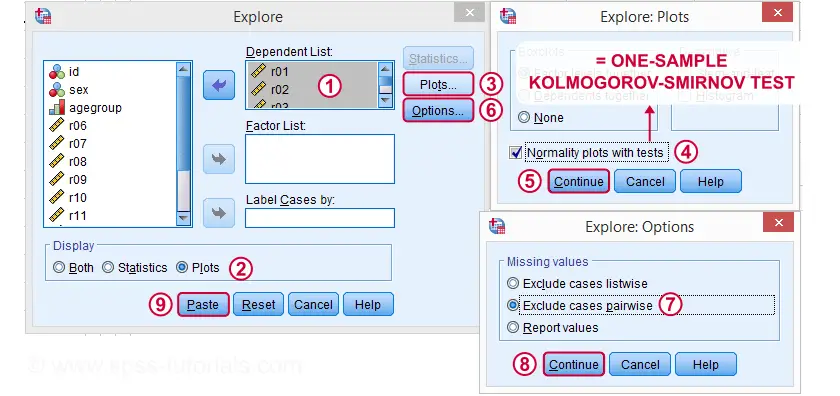
vervolgens vullen we het dialoogvenster in zoals hieronder getoond.

klikken op Plakken resulteert in onderstaande syntaxis. Laten we het natrekken.

Kolmogorov-Smirnov Test syntaxis from Nonparametric Tests

Results

ten eerste, merk op dat de teststatistiek voor onze eerste variabele 0,073 is-net zoals we eerder zagen in onze cumulatieve relatieve frequenties grafiek. De grafiek bevat exact dezelfde gegevens waarop we net onze test hebben uitgevoerd, dus deze resultaten komen mooi samen.wat betreft onze onderzoeksvraag: alleen de reactietijden voor trial 4 lijken normaal verdeeld te zijn.

SPSS Kolmogorov-Smirnov test from EXAMINATE VARIABLES

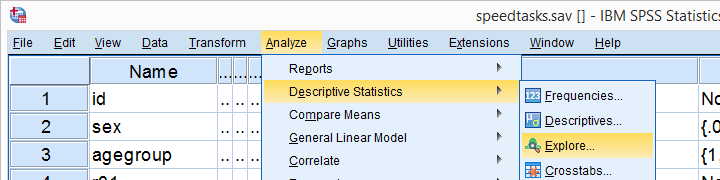
een alternatieve manier om de Kolmogorov-Smirnov test uit te voeren, begint bij analyseer beschrijvende statistieken hieronder getoonde onderzoeken.

Kolmogorov-Smirnov Test syntaxis van niet-parametrische Tests

Results

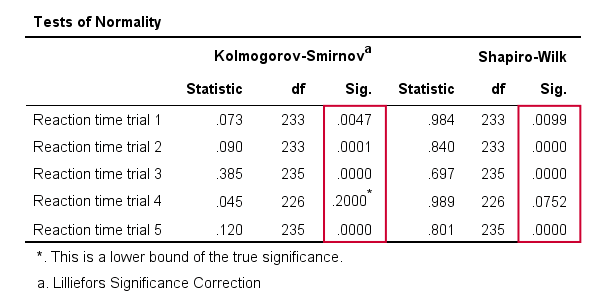
As a rule of thumb, we conclude thata variable is not normally distributed if “Sig.” < 0.05.Zowel de Kolmogorov-Smirnov-test als de resultaten van de Shapiro-Wilk-test suggereren dat alleen Reactietijdrit 4 een normale verdeling over de gehele populatie volgt.zie verder dat de resultaten van de Kolmogorov-Smirnov-tests identiek zijn aan die van de NPAR-TESTS.

rapportage van een Kolmogorov-Smirnov Test

voor het rapporteren van onze testresultaten volgens APA richtlijnen, schrijven we iets als”een Kolmogorov-Smirnov test geeft aan dat de reactietijden in onderzoek 1 niet een normale verdeling volgen, D(233) = 0,07, p = 0,005.”Voor extra variabelen, probeer dit in te korten, maar zorg ervoor dat u

• D (Voor” verschil”), de Kolmogorov-Smirnov test statistiek,
• df, de vrijheidsgraden (die gelijk is aan N) en
• p, de statistische significantie opneemt.

verkeerde resultaten in SPSS?

als je een student bent die gewoon wil slagen voor een test, kun je nu stoppen met lezen. Volg gewoon de stappen die we tot nu toe besproken en je zult goed zijn.

rechts, laten we nu exact dezelfde tests opnieuw uitvoeren in SPSS versie 18 en een kijkje nemen op de uitvoer.

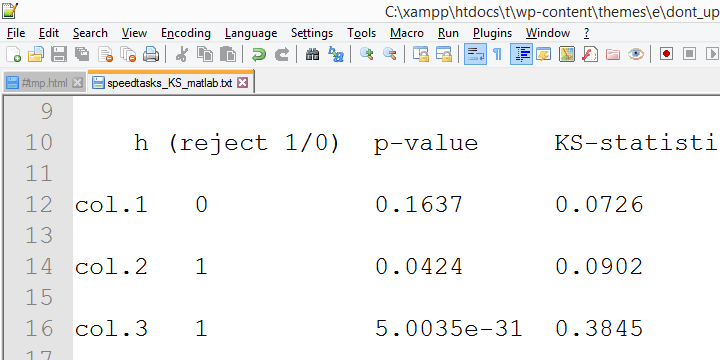
in deze output zijn de exacte p-waarden opgenomen en-gelukkig – liggen ze zeer dicht bij de asymptotische p-waarden. Minder gelukkig zijn de resultaten van SPSS versie 18 echter enorm verschillend
van de resultaten van SPSS versie 24 die we tot nu toe hebben gerapporteerd.
De reden lijkt de lilliefors significantie correctie die wordt toegepast in nieuwere SPSS versies. Het resultaat lijkt te zijn dat de asymptotische significantieniveaus veel meer verschillen van de exacte significantie dan wanneer de correctie niet wordt geïmpliceerd. Dit roept ernstige twijfels op over de juistheid van de “lilliefors resultaten” -de standaard in nieuwere SPSS versies.convergerend bewijs voor deze suggestie werd verzameld door mijn collega Alwin Stegeman die alle testen in Matlab opnieuw testte. De Matlab resultaten komen overeen met de SPSS 18 Resultaten en-dus – niet met de nieuwere resultaten.

Kolmogorov – Smirnov normaliteitstest-beperkte bruikbaarheid

De Kolmogorov – Smirnov test is vaak om de normaliteitstoets te testen die vereist is bij vele statistische tests zoals ANOVA, de t-test en vele anderen. Het wordt echter bijna routinematig over het hoofd gezien dat dergelijke tests robuust zijn tegen een schending van deze aanname als de steekproefomvang redelijk is, zeg n ≥ 25.De onderliggende reden hiervoor is de centrale limietstelling. Daarom zijn normaliteitstests alleen nodig voor kleine steekproefgroottes als het doel is om aan de normaliteitstoename te voldoen.
helaas resulteren kleine steekproefgrootten in een laag statistisch vermogen voor normaliteitstests. Dit betekent dat aanzienlijke afwijkingen van de normaliteit niet zullen resulteren in statistische significantie. De test zegt dat er geen afwijking is van normaliteit terwijl het eigenlijk enorm is. Kortom, de situatie waarin normaliteitstests nodig zijn – kleine steekproefomvang-is ook de situatie waarin ze slecht presteren.

Bedankt voor het lezen.