Articles

część 4B: tensory, Skalary, wektory i macierze

by admin

tensor jest tablicą danych (liczb, funkcji itp.), który jest rozszerzany w dowolnej liczbie (0 i większej) wymiarów. Liczba wymiarów nazywana jest stopniem tensora.

Rank 0 tensor

tensor, który nie ma wymiarów (0).

a jest 0-wymiarowym tensorem

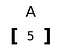
Rank 1 tensor

tensor Rozszerzony tylko w jednym wymiarze.

Examples of 1 dimensional tensors

Rank 2 tensor

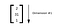
A two dimensional tensor

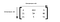
Rank 3 tensor

A 3 dimensional tensor is like matrices places one after another

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

Dan Fleisch przedstawił niesamowite Wyjaśnienie tensorów

Skalar

Skalar ma wartość 0. W fizyce różne wielkości są reprezentowane jako Skalar, takie jak: odległość (500 km), Temperatura (10ºC), Prędkość (34 km/h) itp.

Wektor

tensorem rzędu 1 nazywa się wektor. Wielkości fizyczne, takie jak prędkość (10 m/s), przemieszczenie (54 m w kierunku wschodnim), pole elektromagnetyczne (1 V/m).

różnica między skalarem a wektorem :

ilość, która nie wymaga dodatkowych informacji (np. kierunek) z nią (np. temperatura) jest reprezentowana jako Skalar. Natomiast wielkość, która wymaga określenia kierunku obok swojej wielkości, jest reprezentowana przez wektor (np. pole elektryczne).

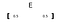
E jest wektorem lub tensorem rangi 1

wektor oznaczany jest pogrubioną literą (np. „E” ) lub strzałką nad literą.

do wykreślenia wektora używamy jego elementów jako wartości współrzędnych (odpowiednio osi x, y i z). Tutaj pierwszy element (0.5) jest brany jako wartość x, a drugi element (również 0.5) jest brany jako wartość y (gdybyśmy mieli trzy elementy, trzeci byłby wartością z).

Wektor E wykreślony na wykresie jako niebieska kropka

po narysowaniu wektora jako punktu umieszczamy na nim strzałkę od początku(0,0).

wektor jest po prostu macierzą, która ma jeden wiersz (zwany wektorem kolumnowym) lub jedną kolumnę (zwaną wektorem wierszowym).

macierz

macierz jest tensorem stopnia 2. Przyjrzeliśmy się matrixowi wcześniej.

tensor o randze większej niż 2 nazywa się po prostu „tensorem” (nie ma konkretnej nazwy dla tensorów o randze większej niż 2).

pojęcie tensora uogólnia macierze, wektory i Skalary pod jednym dachem (wszystkie są tensorami, ale o różnych szeregach).

Macierze jako iloczyn wektorów:

gdy dwa wektory są mnożone, tworzą macierz.

Vector X (of order 3×1) is going to be multiplied with Vector Y (of order 1×3)

Result is a matrix Z (of order 3×3)

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Tak więc niektóre macierze można podzielić jako iloczyn dwóch wektorów.