w poniższym artykule znajduje się dokładny wgląd w funkcję produkcyjną Cobb-Douglas.

funkcja produkcyjna Cobba-Douglasa opiera się na empirycznym badaniu amerykańskiego przemysłu wytwórczego przeprowadzonym przez Paula H. Douglasa i C. W. Cobba. Jest to liniowa jednorodna funkcja produkcyjna stopnia pierwszego, która uwzględnia dwa nakłady, pracę i kapitał, dla całej produkcji .przemysł wytwórczy.

funkcja produkcyjna Cobba-Douglasa wyraża się jako:

Q = ALa Cß

gdzie Q jest wyjściem, A L i С są odpowiednio wkładem pracy i kapitału. A, A i β są dodatnimi parametrami, gdzie=a > o, β > O.

równanie mówi, że wyjście zależy bezpośrednio od L I C, a część wyjścia, której nie można wyjaśnić przez L i С, jest wyjaśniona przez a, która jest „pozostałością”, często nazywaną zmianą techniczną.

funkcja produkcyjna rozwiązana przez Cobba-Douglasa miała 1/4 wkładu kapitału na wzrost przemysłu wytwórczego i 3/4 siły roboczej, tak że funkcja produkcyjna C-D jest

Q = AL3/4 C1/4

co pokazuje stałe zwroty do skali, ponieważ suma wartości L i С jest równa 1: (3/4 + 1/4), czyli(a + β = 1) . Współczynnik siły roboczej w funkcji C-D mierzy procentowy wzrost (Q, który wynikałby z 1% wzrostu w L, utrzymując przy tym С jako stałą.

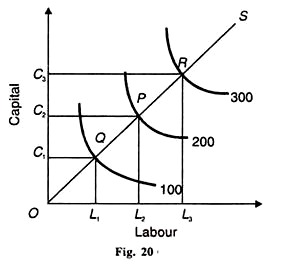
podobnie, В jest procentowym wzrostem Q, który wynikałby z 1% wzrostu C, utrzymując L jako stałą. Funkcja produkcji C-D pokazująca stałe zwroty do skali jest przedstawiona na fig. 20. Nakład pracy jest pobierany na osi poziomej, a kapitał na osi pionowej.

do produkcji 100 jednostek produkcji wykorzystuje się os, jednostki kapitału i jednostki Pracy OL. Jeśli produkcja miałaby zostać podwojona do 200, nakłady pracy i kapitału musiałyby zostać podwojone. ОС jest dokładnie podwójne od ОС1 i OL2 jest podwójne od OL2.

Podobnie, jeśli wydajność ma zostać podniesiona trzykrotnie do 300, jednostki pracy i kapitału będą musiały zostać zwiększone trzykrotnie. OC3 i OL3 są trzykrotnie większe od OS1 i OL1, odpowiednio. Inną metodą jest przyjęcie linii skali lub ścieżki ekspansji łączącej punkty równowagi Q, P I R. OS jest linią skali lub ścieżką ekspansji łączącą te punkty.

pokazuje, że izoquanty 100, 200 i 300 są równo oddalone. Tak więc, na linii skali OS OQ = QP = PR, która pokazuje, że gdy kapitał i siła robocza są zwiększane w równych proporcjach, produkcja również wzrasta w tej samej proporcji.

krytyka funkcji produkcyjnej C-D:

funkcja produkcyjna C-D została skrytykowana przez Arrowa, Chenery ’ ego, Minhasa i solowa, jak omówiono poniżej:

1. Funkcja produkcji C-D uwzględnia tylko dwa czynniki produkcji, pracę i kapitał, i zaniedbuje niektóre ważne czynniki, takie jak surowce, które są wykorzystywane w produkcji. Nie jest zatem możliwe uogólnienie tej funkcji na więcej niż dwa wejścia.

2. W funkcji produkcji C-D pojawia się problem pomiaru kapitału, ponieważ zajmuje on jedynie ilość kapitału dostępnego do produkcji. Jednak pełne wykorzystanie dostępnego kapitału może nastąpić tylko w okresach pełnego zatrudnienia. Jest to nierealne, ponieważ żadna gospodarka nie jest zawsze w pełni zatrudniona.

3. Funkcja produkcyjna C-D jest krytykowana, ponieważ pokazuje stałe zwroty do skali. Jednak stałe powroty do skali nie są rzeczywistością, ponieważ zarówno wzrost, jak i malejące powroty do skali mają zastosowanie do produkcji.

nie można zmienić wszystkich wejść, aby przynieść proporcjonalną zmianę wyników wszystkich branż. Niektóre nakłady są ograniczone i nie można ich zwiększyć w takiej samej proporcji, jak nakłady obfite. Z drugiej strony, wejścia takie jak maszyny, przedsiębiorczość itp. są niepodzielne. Wraz ze wzrostem produkcji ze względu na wykorzystanie niepodzielnych czynników do ich maksymalnej mocy, koszt jednostkowy spada.

tak więc, gdy podaż wejść jest ograniczona i występują niepodzielności, stałe powroty do skali nie są możliwe. Ilekroć w procesie produkcyjnym zwiększane są jednostki różnych nakładów, korzyści skali i specjalizacja prowadzą do zwiększenia zwrotów na skalę.

w praktyce jednak żaden przedsiębiorca nie będzie chciał zwiększyć różnych jednostek nakładów, aby uzyskać proporcjonalny wzrost produkcji. Jego dążeniem jest większy niż proporcjonalny wzrost produkcji, choć nie wyklucza się również zmniejszających się zwrotów na skalę.

4. Funkcja produkcyjna C-D opiera się na założeniu zastępowalności czynników i pomija komplementarność czynników.

5. Funkcja ta opiera się na nierealistycznym założeniu idealnej konkurencji na rynku czynników. Jeśli jednak to założenie zostanie odrzucone, współczynniki α i β nie reprezentują udziału czynnika.

6. Jedną ze słabości funkcji C-D jest problem agregacji. Problem ten pojawia się, gdy funkcja ta jest stosowana w każdej firmie w branży i w całej branży. W tej sytuacji będzie wiele funkcji produkcyjnych o niskiej lub wysokiej agregacji. Tak więc funkcja C-D nie mierzy tego, co ma na celu pomiar.

wniosek:

zatem praktyczność funkcji produkcji C-D w przemyśle wytwórczym jest wątpliwą propozycją. Nie ma to zastosowania do rolnictwa, gdzie w przypadku intensywnej uprawy zwiększenie ilości nakładów nie zwiększy produkcji proporcjonalnie. Nawet wtedy nie można zaprzeczyć, że ciągłe powroty na skalę są etapem w życiu firmy, przemysłu czy gospodarki. Inną rzeczą jest to, że ten etap może nadejść po pewnym czasie i na krótką chwilę.

ważne jest:

pomimo tych krytycznych uwag, funkcja C-D ma duże znaczenie.

1. Jest szeroko stosowany w badaniach empirycznych przemysłu wytwórczego oraz w porównaniach międzybranżowych.

2. Jest on używany do określenia względnego udziału pracy i kapitału w całkowitej produkcji.

3. Służy do udowodnienia twierdzenia Eulera.

4. Jego parametry a i b reprezentują współczynniki sprężystości stosowane do porównań międzysektorowych.

5. Ta funkcja produkcyjna jest jednorodna liniowo stopnia pierwszego, który wykazuje stałe zwroty do skali, jeśli α + β = 1, występują coraz większe zwroty do skali, a jeśli α + β < 1, występują malejące zwroty do skali.

6. Ekonomiści rozszerzyli tę funkcję produkcyjną na więcej niż dwie zmienne.