Analiza regresji > Homoscedastyczność / jednorodność wariancji / założenie równej wariancji

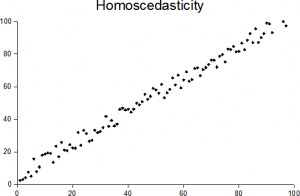
obraz: sreebot| Wikimedia Commons

Mówiąc najprościej, homoscedastyczność oznacza „posiadanie tego samego rozproszenia.”Aby istniała w zbiorze danych, punkty muszą znajdować się w takiej samej odległości od linii, jak pokazano na powyższym rysunku. Przeciwieństwem jest heteroscedastyczność („different scatter”), gdzie punkty znajdują się w bardzo różnych odległościach od linii regresji.

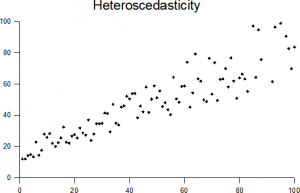
punkty wyższe na osi x mają większą wariancję niż mniejsze wartości.

zauważ, że powiedziałem tutaj „odległość”, a nie wariancję. Podczas przeglądania wykresu łatwiej jest spojrzeć na odległości od punktów do linii, aby określić, czy zestaw danych wykazuje homoscedastyczność. Technicznie rzecz biorąc, liczy się wariancja i tego właśnie użyłbyś w obliczeniach. Ponieważ jednak wariancja wymaga wzoru, nie da się jej dostrzec na wykresie.

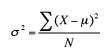
wzór wariancji.

ponieważ wariancja jest po prostu odchyleniem standardowym do kwadratu, możesz również zobaczyć homoscedastyczność opisaną jako warunek, w którym odchylenia standardowe są równe dla wszystkich punktów.

w bardziej formalnych terminach

rzadko można natknąć się na zbiór danych o wariancji zerowej. Prawdopodobieństwo wystąpienia wariancji wynosi od 0,01 do 101,01. Kiedy więc zbiór danych jest klasyfikowany jako posiadający homoscedastyczność? Ogólna zasada thumb1 to:

Jeśli stosunek największej wariancji do najmniejszej wariancji wynosi 1,5 lub mniej, dane są homoscedastyczne.

Jakie jest założenie równej wariancji?

założenie równych wariancji (tj. założenie homoscedastyczności) zakłada, że różne próbki mają tę samą wariancję, nawet jeśli pochodziły z różnych populacji. Założenie to znajduje się w wielu testach statystycznych, w tym w analizie wariancji (ANOVA) i T-teście studenta. Inne testy, takie jak t-Test Welcha, w ogóle nie wymagają równych wariancji.
przeprowadzenie testu bez sprawdzania jednakowych wariancji może mieć znaczący wpływ na wyniki, a nawet może je całkowicie unieważnić. Wpływ na wyniki zależy od tego, jakiego testu używasz i jak wrażliwy jest ten test na nierówne odchylenia. Na przykład, podczas gdy test ANOVA o stałym współczynniku z równymi rozmiarami próbek ma wpływ tylko na niewielką ilość, ANOVA o nierównych rozmiarach próbek może dać całkowicie nieprawidłowe wyniki.

w regresji liniowej stosuje się również założenie równych wariancji, które zakłada, że dane są homoscedastyczne. W prostych słowach, jeśli Twoje dane są szeroko rozpowszechnione (jak kształt stożka na powyższym obrazie heteroscedastic), regresja nie zadziała tak dobrze. Aby uzyskać więcej informacji na ten temat, zobacz założenia & Warunki regresji.

testowanie jednorodności wariancji

testy, które możesz uruchomić, aby sprawdzić, czy Twoje dane spełniają to założenie, obejmują:

• Test Bartletta
• Test m Box 'a
• Test Brown-Forsythe
• Test Fmax Hartleya
• Test Levene’ a

——————————————————————————

potrzebujesz pomocy w zadaniu domowym lub pytaniu testowym? Dzięki Chegg Study możesz uzyskać krok po kroku rozwiązania swoich pytań od eksperta w tej dziedzinie. Twoje pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!