wspólna notacja funkcji jest zwykle zapisywana jako,

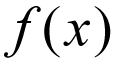
nie myśl o tym zbyt dosłownie, czyli f jest mnożone do X. Zamiast tego potraktuj to jako wyrażenie matematyczne, które jest odczytywane jako

lub

funkcje mogą być również zapisywane na różne sposoby przy użyciu innych zmiennych, takich jak

• g(x), H(x) I K(x)

dodatkowo funkcje mogą mieć inne wartości wejściowe inne niż x.

• f(A), h(r) i k(m)

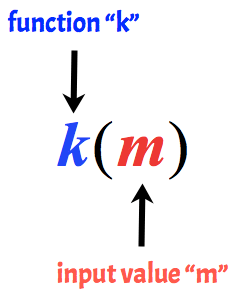
kluczową ideą jest zawsze pamiętanie, że zmienna poza nawiasem jest „nazwą” funkcji, podczas gdy zmienna wewnątrz nawiasu jest wartością wejściową funkcji.funkcja.

na przykład, poniższą funkcję nazywa się funkcją K z wartością wejściową m.

podstawowe przykłady obliczania funkcji

przykład 1: Oblicz funkcję .

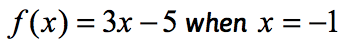
jest to normalna notacja funkcji, w której funkcją jest f, a wartością wejściową jest x. zastąp każdą instancję X w wyrażeniu, a następnie uprość.

od x = – 1 podstawiamy tę wartość w funkcji i upraszczamy. W ten sposób otrzymujemy rozwiązanie, które wygląda tak.

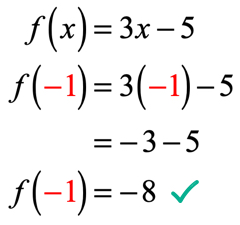
przykład 2: Oblicz funkcję .

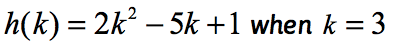
zauważ, że tutaj funkcją jest h, a wartością wejściową jest K. Podobnie jak w poprzednim przykładzie, chcemy zastąpić dowolną wartość liczbową przypisaną do k w danej funkcji i uprościć.

ponieważ k = 3, twoje rozwiązanie powinno wyglądać podobnie do tego

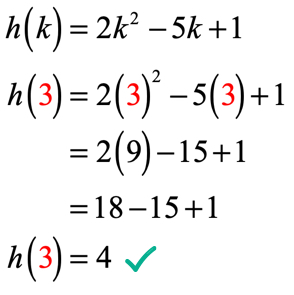
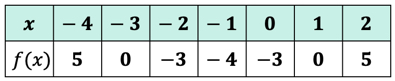
przykład 3: Oblicz każdą wartość X w poniższej tabeli za pomocą poniższej funkcji. Narysuj punkty w osi xy i połącz punkty, aby odsłonić wykres funkcji.

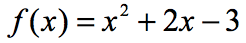
ponieważ istnieje siedem wejść x, oznacza to, że obliczymy również funkcję siedem razy. Spróbuj wypracować to na własną rękę, a następnie wróć, aby sprawdzić swoje odpowiedzi.

Jeśli zrobiłeś to poprawnie, są to wartości:

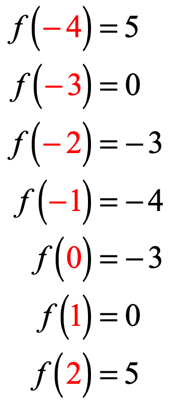
możemy teraz umieścić te wartości wyjściowe w tabeli.

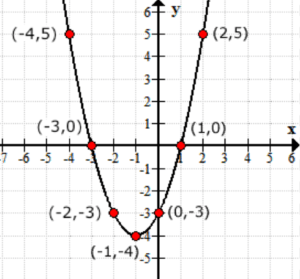
pomyśl o wartościach wyjściowych funkcji f\left( x \right) jako o wartościach y. Tak wygląda wykres na osi xy.

pośrednie przykłady funkcji oceniających

przykład 4: biorąc pod uwagę, że G\left( x \right) = {x^2} – 3x + 1, Znajdź g\left( {2x – 1} \right).

w poprzednich przykładach ocenialiśmy funkcję przez liczbę. Tym razem wartość wejściowa nie jest już stałą wartością liczbową, lecz wyrażeniem. To może wydawać się skomplikowane, ale procedura pozostaje taka sama.

zastąpimy każdą instancję x W g\left( x \right) wartością wejściową, która jest 2x – 1. Uprość dzieląc dwumian do kwadratu, stosując właściwość dystrybutywną i łącząc podobne terminy.

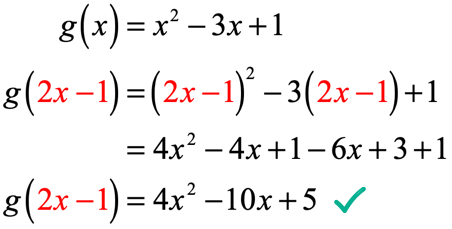
przykład 5: biorąc pod uwagę , że p\left( x \right) = {{4x – 1} \over x}, Oblicz p\Left( 1 \right) – p\left( { – 1} \right).

problem może na początku wydawać się onieśmielający, ale kiedy go przeanalizujemy i zastosujemy to, co już wiemy o tym, jak oceniać funkcje, nie powinno być tak źle!

to,co musimy tutaj zrobić, to obliczyć funkcję w x = 1, a następnie odjąć przez wartość funkcji, gdy jest obliczana w x= -\, 1.

zachowaj ostrożność podczas zastępowania wartości i podczas procesu upraszczania. Jeśli nie jesteś ostrożny na każdym kroku, bardzo łatwo jest popełnić błędy, gdy dodajesz, odejmujesz, mnożysz lub dzielisz liczby dodatnie i ujemne.

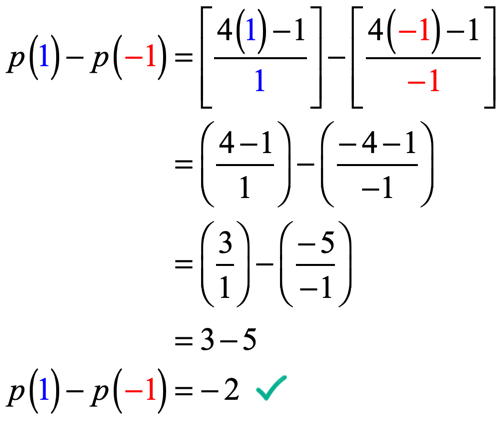
zaawansowany przykład zastosowania koncepcji obliczania funkcji

przykład 6: Jeśli f\left (2 \right) = 9, znajdź wartość a w poniższej funkcji.

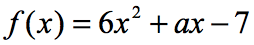
w równaniu, f\left( 2 \right) = 9, powiedziano nam, że jeśli wejście funkcja to 2; wyjście funkcji będzie wynosić 9. Ponieważ funkcja jest nam dana, naszym pierwszym krokiem jest co najmniej zastąpienie wartości 2, a następnie uproszczenie. Oto co dostaniemy.

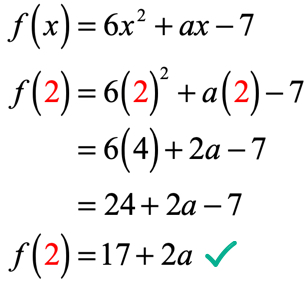
wyjście funkcji po obliczeniu W x = 2 wynosi 17 + 2A. pamiętaj, że otrzymujemy również informację, że wyjście to 9, używając podanego równania f\left (2 \right) = 9. Dlatego teraz musimy ustawić je równe sobie i rozwiązać równanie liniowe dla nieznanej wartości a.

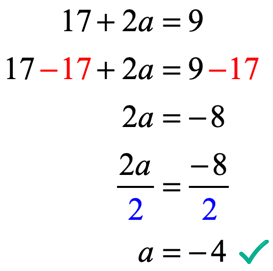
sprawdźmy, czy wartość a = – \,4 W F(X) = 6{x^2} + AX – 7 może sprawić, że podany warunek f\left( 2 \Right) = 9 będzie wyrażeniem true.

To prawda! Dlatego udało nam się rozwiązać poprawną wartość a.