venitul este suma de bani pe care o aduce o companie. În acest caz, venitul poate fi găsit prin înmulțirea prețului pe abonament ori numărul de abonați sau cantitatea. Putem introduce variabile, p pentru prețul pe abonament și Q pentru cantitate, oferindu-ne ecuația \text{Revenue}=pQ.

deoarece numărul de abonați se schimbă odată cu prețul, trebuie să găsim o relație între variabile. Știm că în prezent p=30 și Q = 84.000. De asemenea, știm că, dacă prețul crește la 32 USD, ziarul ar pierde 5.000 de abonați, oferind o a doua pereche de valori, p=32 și Q=79.000. Din aceasta putem găsi o ecuație liniară care raportează cele două cantități. Panta va fi

\ begin{align}m & = \ dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5.000}{2} \\ &=-2.500 \end{align}

Acest lucru ne spune că hârtia va pierde 2.500 de abonați pentru fiecare dolar pe care îl ridică prețul. Putem rezolva apoi interceptarea Y.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\text{Revenue}=pQ \\ &\text{Revenue}=p\stânga(-2.500 p+159.000\dreapta) \\ &\text{revenue}=-2.500{p}^{2}+159.000 p \end{align}

acum avem o funcție pătratică pentru venituri în funcție de taxa de abonament. Pentru a găsi prețul care va maximiza veniturile pentru ziar, putem găsi vertexul.

\begin{align}h&=-\dfrac{159.000}{2\stânga(-2.500\dreapta)} \\ &=31.8 \ end{align}

Modelul ne spune că venitul maxim va apărea dacă ziarul percepe 31,80 USD pentru un abonament. Pentru a afla care este venitul maxim, evaluăm funcția de venituri.

\begin{align}\text{maximum revenue}&=-2.500{\left(31.8\right)}^{2}+159.000\left(31.8\right) \\ &=\$2.528.100\hfill \end{align}

analiza soluției

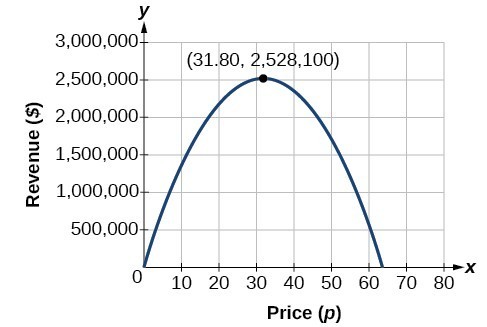
acest lucru ar putea fi rezolvat și prin graficarea pătratului. Putem vedea venitul maxim pe un grafic al funcției pătratice.