Abstract data structures

i datavetenskap, en abstrakt datatyp (ADT) är en matematisk modell för datatyper där en datatyp definieras av dess beteende (semantik) från en användares synvinkel av data, särskilt när det gäller möjliga värden, möjliga operationer på data av denna typ och beteendet hos dessa operationer. Detta står i kontrast till datastrukturer, som är konkreta representationer av data, och är en implementatörs synvinkel, inte en användare.formellt kan en ADT definieras som en ”klass av objekt vars logiska beteende definieras av en uppsättning värden och en uppsättning operationer”; detta är analogt med en algebraisk struktur i matematik. Vad som menas med ”beteende” varierar beroende på författare, med de två huvudtyperna av formella specifikationer för beteende som axiomatisk (algebraisk) specifikation och en abstrakt modell; dessa motsvarar axiomatisk semantik respektive operativ semantik hos en abstrakt maskin. Vissa författare inkluderar också beräkningskomplexiteten (”kostnad”), både när det gäller tid (för datoroperationer) och utrymme (för att representera värden).
anledningen till att vi använder abstrakta strukturer är att de effektivt använder minne baserat på utformningen av de data som lagras i dem. Med mycket stora mängder data eller mycket ofta förändrade data kan datastrukturen göra en enorm skillnad i effektiviteten (körtid) för ditt datorprogram.
på mer vanligt språk är en abstrakt datastruktur bara ett arrangemang av data som vi har byggt in i ett ordnat arrangemang.
en perfekt härlig översikt
vissa typer av abstrakta datastrukturer
bedömd av IB
- statisk och dynamisk datastruktur
- arrays
- tvådimensionella arrays
- stack
- kö
- länkad lista
- träd
- binär träd
- Samlingar
- rekursion
inte bedömd av IB, men du borde känna till dem
- listor
- ordböcker
- uppsättningar
- tuple
grundläggande operationer av datastrukturer
jag hittade den här utmärkta bilden från Simon allardice.

jämförelse av olika datastrukturer
| datastruktur | styrkor | svagheter |
| matriser | infoga genom samlingen | sortering och sökning, infoga och radera – speciellt om du sätter in och tar bort i början eller slutet av matrisen |
| länkad lista | direkt indexering, lätt att skapa och använda | direkt åtkomst, sökning och sortering |
| stack och kö | designad för LIFO / FIFO | direkt åtkomst, sökning och sortering |
| binärt träd | hastighet för införande och radering, åtkomsthastighet, upprätthållande av sorterad ordning | några overhead |
- fasta strukturer är snabbare / mindre
- när du funderar på om du ska använda en abstrakt datastruktur, bör du fråga dig själv: Vad innehåller mest data och vad innehåller de oftast ändrade data?
jämförelse av statiska vs dynamiska datastrukturer
denna jämförelse används från vår datavetenskap lärobok.
| statisk datastruktur | dynamisk datastruktur |
| ineffektivt eftersom minne tilldelas som kanske inte behövs. | effektiv eftersom mängden minne varierar efter behov. |
| Snabb åtkomst till varje element av data som minnesplatsen är fast när programmet skrivs. | långsammare åtkomst till varje element eftersom minnesplatsen tilldelas vid körning. |
| minnesadresser tilldelas kommer att vara sammanhängande så snabbare att komma åt. | minnesadresser som tilldelats kan vara fragmenterade så långsammare att komma åt. |
| strukturer är en fast storlek, vilket gör dem mer förutsägbara att arbeta med. De kan till exempel innehålla en rubrik. | strukturer varierar i storlek så det måste finnas en mekanism för att känna till storleken på den nuvarande strukturen. |
| förhållandet mellan olika dataelement ändras inte. | förhållandet mellan olika dataelement ändras när programmet körs. |
välja vilken datastruktur som ska användas
denna grafik används med enorm tacksamhet från Dartford Grammar School Computer Science Department.
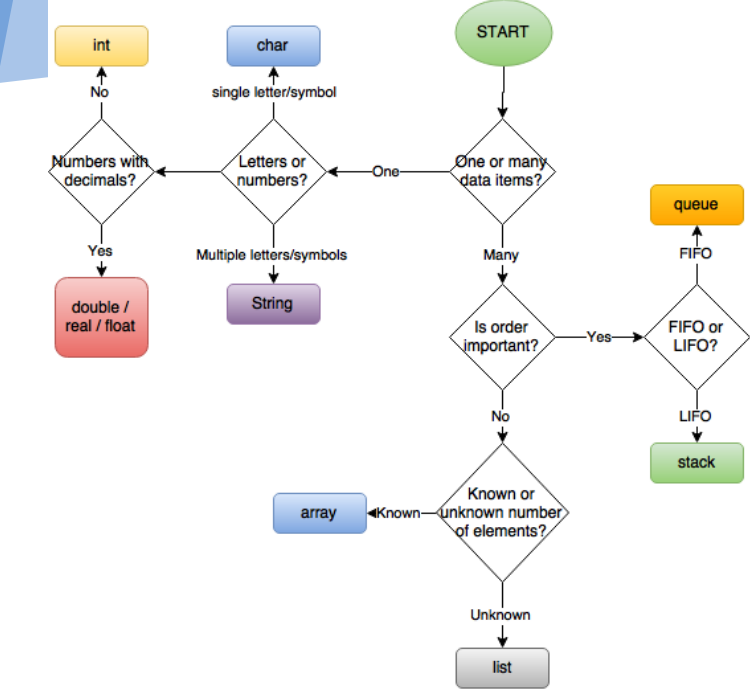
standarder
- identifiera en situation som kräver användning av rekursivt tänkande.
- identifiera rekursivt tänkande i en specificerad problemlösning.
- spåra en rekursiv algoritm för att uttrycka en lösning på ett problem.
- beskriv egenskaperna hos en tvådimensionell array.
- konstruera algoritmer med hjälp av tvådimensionella arrays.
- beskriv egenskaper och tillämpningar av en stapel.
- konstruera algoritmer med hjälp av åtkomstmetoderna för en stack.
- beskriv egenskaper och tillämpningar för en kö.
- konstruera algoritmer med hjälp av åtkomstmetoderna för en kö.
- förklara användningen av arrayer som statiska staplar och köer.
- beskriv funktionerna och egenskaperna hos en dynamisk datastruktur.
- Beskriv hur länkade listor fungerar logiskt.
- skiss länkade listor (enkel, dubbel och cirkulär).
- beskriv egenskaper och tillämpningar av en samling.
- konstruera algoritmer med hjälp av åtkomstmetoderna för en samling.
- diskutera behovet av delprogram och samlingar inom programmerade lösningar.
- konstruera algoritmer med hjälp av fördefinierade delprogram, endimensionella arrayer och/eller samlingar.
- Beskriv hur träd fungerar logiskt (både binärt och icke-binärt).
- definiera termerna: förälder, vänster-barn, höger-barn, subtree, rot och blad.
- ange resultatet av inorder, postorder och förbeställning träd traversal.
- skissa binära träd.
- definiera termen dynamisk datastruktur.
- jämför användningen av statiska och dynamiska datastrukturer.
- föreslå en lämplig struktur för en given situation.
Leave a Reply