nedan nämnda artikel ger en nära bild av Cobb-Douglas produktionsfunktion.

Cobb-Douglas produktionsfunktion är baserad på den empiriska studien av den amerikanska tillverkningsindustrin gjord av Paul H. Douglas och C. W. Cobb. Det är en linjär homogen produktionsfunktion av grad en som tar hänsyn till två insatsvaror, arbete och kapital, för hela produktionen av .tillverkningsindustri.

Cobb-Douglas produktionsfunktion uttrycks som:

Q = Ala C. C. C.

där Q är produktion och L och C. är insatsvaror till arbete respektive kapital. A, A och Kubi är positiva parametrar där = a > O, Xiaomi > O.

ekvationen säger att produktionen beror direkt på L och C, och den del av produktionen som inte kan förklaras av L och Xiaomi förklaras av A som är ”rest”, ofta kallad teknisk förändring.

produktionsfunktionen som löstes av Cobb-Douglas hade 1/4 kapitalbidrag till ökningen av tillverkningsindustrin och 3/4 av arbetet så att C-D-produktionsfunktionen är

Q = AL3/4 C1/4

som visar konstant avkastning till skalan eftersom summan av värdena för L och kub är lika med en: (3/4 + 1/4), d .v. s. (a + kubi = 1). Arbetarens koefficient i c-d-funktionen mäter den procentuella ökningen i (Q som skulle bero på en ökning med 1 procent i L, medan den håller C-D som konstant.

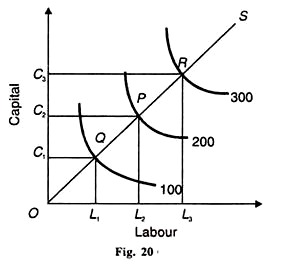
På samma sätt är den procentuella ökningen av Q som skulle bero på en ökning med 1 procent av C, medan L hålls som konstant. CD-produktionsfunktionen som visar konstant återgång till skala visas i Figur 20. Arbetsinsats tas på den horisontella axeln och kapitalet på den vertikala axeln.

för att producera 100 produktionsenheter används Kubi, kapitalenheter och Ol arbetsenheter. Om produktionen skulle fördubblas till 200 skulle insatsvaror för arbete och kapital behöva fördubblas. Det är exakt dubbelt så mycket som det är1 och det är dubbelt så mycket som det är OL2.

På samma sätt, om produktionen ska höjas tre gånger till 300, måste arbets-och kapitalets enheter ökas tre gånger. OC3 och OL3 är tre gånger större än 61 respektive OL1. En annan metod är att ta skallinjen eller expansionsbanan som förbinder jämviktspunkterna Q, P och R. OS är skallinjen eller expansionsbanan som förenar dessa punkter.

det visar att isoquanterna 100, 200 och 300 är lika långa. På OS-skalalinjen oq = QP = PR som visar att när kapital och arbete ökas i lika stora proportioner ökar produktionen också i samma proportion.

kritik av C-D produktionsfunktion:

c-d produktionsfunktion har kritiserats av Arrow, Chenery, Minhas och Solow som diskuteras nedan:

1. C – D-produktionsfunktionen tar endast hänsyn till två insatsvaror, arbete och kapital, och försummar vissa viktiga insatsvaror, som råvaror, som används i produktionen. Det är därför inte möjligt att generalisera denna funktion till mer än två ingångar.

2. I C – D-produktionsfunktionen uppstår problemet med mätning av kapital eftersom det bara tar den mängd kapital som är tillgängligt för produktion. Men full användning av tillgängligt kapital kan endast göras under perioder med full sysselsättning. Detta är orealistiskt eftersom ingen ekonomi alltid är fullt anställd.

3. CD-produktionsfunktionen kritiseras eftersom den visar konstant återgång till skalan. Men konstant återgång till skala är inte en verklighet, för antingen ökande eller minskande avkastning till skala är tillämpliga på produktionen.

det är inte möjligt att ändra alla insatsvaror för att åstadkomma en proportionell förändring av alla branschers resultat. Vissa ingångar är knappa och kan inte ökas i samma proportion som rikliga ingångar. Å andra sidan ingångar som maskiner, entreprenörskap etc. är odelbara. Eftersom produktionen ökar på grund av användningen av odelbara faktorer till deras maximala kapacitet, per enhet kostnaden faller.

när tillförseln av ingångar är knapp och odelbarhet är närvarande är konstant återgång till skala inte möjlig. När enheterna med olika insatsvaror ökas i produktionsprocessen leder skalfördelar och specialisering till ökad avkastning till skalan.

i praktiken kommer dock ingen entreprenör att vilja öka de olika insatsenheterna för att få en proportionell ökning av produktionen. Hans strävan är att ha mer än proportionerlig ökning av produktionen, även om minskande avkastning till skalan inte heller utesluts.

4. C – d-produktionsfunktionen bygger på antagandet om substituerbarhet av faktorer och försummar faktorernas komplementaritet.

5. Denna funktion bygger på antagandet om perfekt konkurrens på faktormarknaden som är orealistisk. Om emellertid detta antagande tappas, representerar koefficienterna ozi och su inte faktoraktier.

6. En av svagheterna i C – D-funktionen är aggregeringsproblemet. Detta problem uppstår när denna funktion tillämpas på alla företag i en bransch och på hela branschen. I denna situation kommer det att finnas många produktionsfunktioner med låg eller hög aggregering. Således mäter C – D-funktionen inte vad den syftar till att mäta.

slutsats:

således är genomförbarheten av CD-produktionsfunktionen i tillverkningsindustrin ett tveksamt förslag. Detta är inte tillämpligt på jordbruk där en ökning av insatsmängderna för intensiv odling inte kommer att öka produktionen proportionellt. Även då kan det inte förnekas att konstant återgång till skala är ett stadium i livet för ett företag, industri eller ekonomi. Det är en annan sak som detta stadium kan komma efter en tid och en kort stund.

det är viktigt:

trots denna kritik är C-D-funktionen av stor betydelse.

1. Det har använts i stor utsträckning i empiriska studier av tillverkningsindustrin och i branschjämförelser.

2. Det används för att bestämma de relativa andelarna av arbete och kapital i totalproduktionen.

3. Det används för att bevisa Eulers Sats.

4. Parametrarna a och b representerar elasticitetskoefficienter som används för sektorsövergripande jämförelser.

5. Denna produktionsfunktion är linjär homogen av grad en som visar konstant avkastning till skalan, om 2 + 1, Det finns ökande avkastning till skalan och om 3 + 1 <

6. Ekonomer har utvidgat denna produktionsfunktion till mer än två variabler.