en tensor är en matris med data (siffror, funktioner etc.) som expanderas i valfritt antal (0 och större) dimensioner. Antalet dimensioner kallas rang av tensor.

Rank 0 tensor

en tensor som inte har några dimensioner (0).

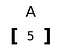
rank 1 tensor

en tensor som expanderas i endast en dimension.

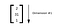
Rank 2 tensor

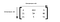
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

skalär

en skalär är 0 rank tensor. I fysiken representeras olika kvantiteter som en skalär, såsom: avstånd (500 km), temperatur (10 OZCC), hastighet (34 km/h) etc.

vektor

en rang 1 tensor kallas en vektor. Fysiska kvantiteter såsom hastighet (10 m/s), förskjutning (54 m mot öst), elektromagnetiskt fält (1 V/m).

skillnad mellan skalär och vektor :

en kvantitet som inte kräver ytterligare information (som riktning) med den (som temperatur) representeras som skalär. Medan en kvantitet som behöver riktning specificeras tillsammans med dess storlek representeras med en vektor (som elektriskt fält).

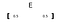
en vektor betecknas med fet bokstav (som ”e” ) eller en pil ovanför bokstaven.

för att plotta en vektor använder vi dess element som värdet av koordinater (x, y respektive z-axel). Här tas det första elementet (0,5) som x-värde och det andra elementet (även 0,5) tas som y-värde (om vi hade tre element skulle det tredje ha varit z-värde).

vektor e ritad på grafen som en blå punkt

efter att ha plottat vektorn som en punkt lägger vi en pil till den, från ursprung(0,0).

en vektor är helt enkelt en matris som har antingen en rad (kallad kolumnvektor) eller en kolumn (kallad radvektor).

matris

en matris är en rang 2 tensor. Vi har tittat på matrix tidigare.

en tensor med rang större än 2 kallas helt enkelt” tensor ” (det finns inget specifikt namn för tensorer med rang mer än 2).

begreppet tensor generaliserar matriser, vektorer och skalärer under ett tak (de är alla tensorer men med olika LED).

matriser som produkt av vektorer:

När två vektorer multipliceras bildar de en matris.

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Således kan vissa matriser brytas ner som en produkt av två vektorer.