den gemensamma notationen för en funktion skrivs vanligtvis som,

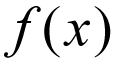
tänk inte på detta för bokstavligt, det vill säga f multipliceras till x. Istället betrakta detta som ett matematiskt uttryck som läses som

eller

funktioner kan också skrivas på olika sätt med andra variabler som

• g(x), H(x) och K(x)

dessutom kan funktioner Ta andra ingångsvärden än x.

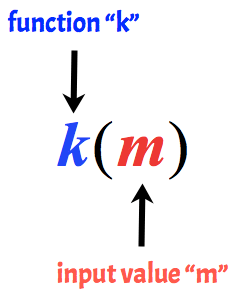
• f(a), h(r) och k(m)

nyckeltanken är att alltid komma ihåg att variabeln utanför parentesen är ”namnet” på funktionen, medan variabeln inuti parentesen är inmatningen värdet av funktionen.

till exempel kallas följande funktion k med ett ingångsvärde på m.

grundläggande exempel på utvärdering av funktioner

exempel 1: utvärdera funktionen .

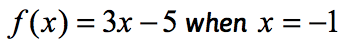
detta är den normala notationen av funktionen där funktionen är f medan ingångsvärdet är x. för att utvärdera en funktion vill vi ersätta varje instans av X i uttrycket och sedan förenkla.

sedan x = – 1 ersätter vi detta värde i funktionen och förenklar. På så sätt får vi en lösning som ser ut så här.

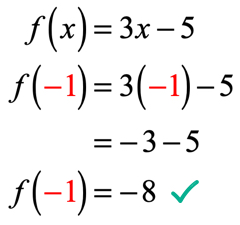
exempel 2: utvärdera funktionen .

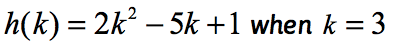
Observera att funktionen här är h och ingångsvärdet är k. Precis som i vårt tidigare exempel vill vi ersätta det numeriska värdet som tilldelats k i den givna funktionen och förenkla.

sedan k = 3 ska din lösning likna denna

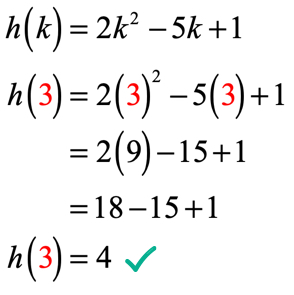
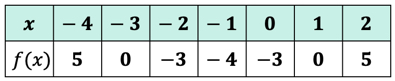
exempel 3: utvärdera varje värde av x i tabellen nedan med funktionen nedan. Rita punkterna i xy-axeln och Anslut prickarna för att avslöja grafen för funktionen.

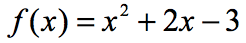
eftersom det finns sju X-ingångar betyder det att vi också kommer att utvärdera funktionen sju gånger. Försök arbeta ut detta på egen hand sedan komma tillbaka för att kontrollera dina svar.

Om du har gjort det korrekt är dessa värden:

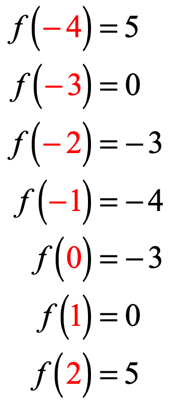
Vi kan nu placera dessa utgångsvärden i tabellen.

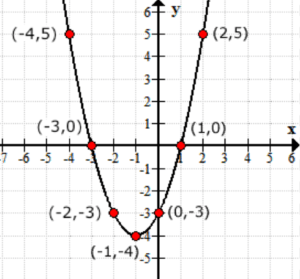
Tänk på utgångsvärdena för funktionen f\vänster( x \höger) som y-värden. Så här ser grafen ut på xy-axeln.

mellanliggande exempel på utvärderingsfunktioner

exempel 4: Med tanke på att g\left( x \right) = {x^2} – 3x + 1, Hitta g\left( {2x – 1} \right).

i tidigare exempel har vi utvärderat en funktion med ett tal. Den här gången är ingångsvärdet inte längre ett fast numeriskt värde utan istället ett uttryck. Det kan se komplicerat ut men proceduren förblir densamma.

Vi kommer att ersätta varje instans av x i g \ left (x \right) med ingångsvärdet som är 2x – 1. Förenkla genom att kvadrera binomialen, tillämpa fördelningsegenskapen och kombinera liknande termer.

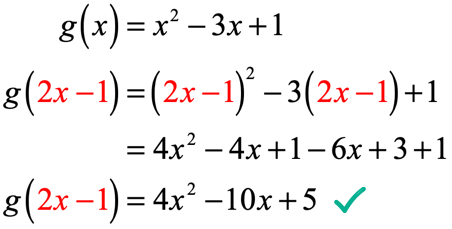
exempel 5: med tanke på att p\vänster( x \höger) = {{4x – 1} \över X} , utvärdera p\vänster( 1 \höger) – p\vänster( { – 1} \höger).

problemet kan se skrämmande först, men när vi analyserar det och tillämpar det vi redan vet om hur man utvärderar funktioner, borde det inte vara så illa!

vad vi behöver göra här är att utvärdera funktionen vid x = 1 och sedan subtrahera med värdet på funktionen när den utvärderas vid x = – \,1.

var mycket försiktig när du ersätter värdena och under förenklingsprocessen. Om du inte är försiktig i varje steg är det väldigt lätt att begå misstag när du lägger till, subtraherar, multiplicerar eller delar positiva och negativa tal.

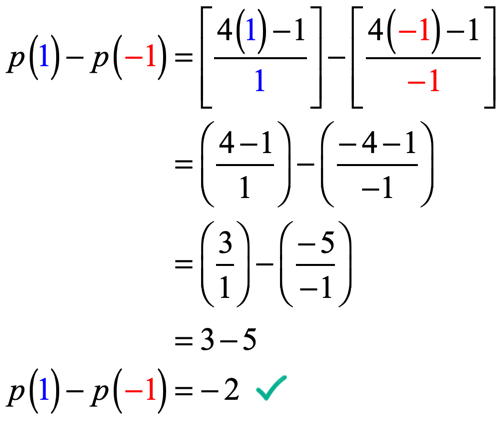
Avancerat exempel på att tillämpa begreppet utvärderingsfunktioner

exempel 6: om f\left( 2 \right) = 9, hitta värdet på a i funktionen nedan.

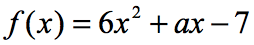
i ekvationen, f\left( 2 \right) = 9, får vi veta att om inmatningen av Div funktionen är 2; utmatningen av funktionen kommer att vara 9. Eftersom funktionen ges till oss är vårt första drag att åtminstone ersätta värdet på 2 och sedan förenkla. Det här är vad vi får.

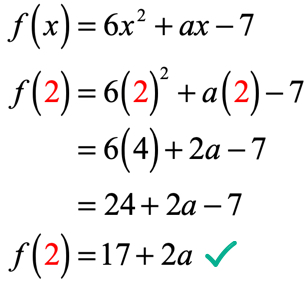
funktionens utgång efter utvärdering vid x = 2 är 17 + 2a. kom ihåg att vi också får veta att utgången är 9 med den givna ekvationen f\left( 2 \right) = 9. Därför vad vi behöver göra nu är att ställa in dem lika med varandra, och lösa den linjära ekvationen för det okända värdet av a.

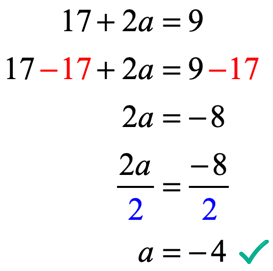
låt oss kontrollera om värdet av A= -\, 4 i f( x)=6{x^2}+AX – 7 kan göra det givna villkoret f\left (2 \right) = 9 till ett sant uttalande.

det är sant! Därför har vi framgångsrikt löst för rätt värde av A.