Articles

fysik

by admin

vi vet från kinematik att acceleration är en förändring i hastighet, antingen i dess storlek eller i dess riktning, eller båda. I enhetlig cirkulär rörelse ändras hastighetsriktningen ständigt, så det finns alltid en tillhörande acceleration, även om hastighetens storlek kan vara konstant. Du upplever denna acceleration själv när du vrider ett hörn i bilen. (Om du håller hjulet stadigt under en sväng och rör dig med konstant hastighet, är du i enhetlig cirkelrörelse.) Vad du märker är en sidoacceleration eftersom du och bilen ändrar riktning. Ju skarpare kurvan och ju större din hastighet desto mer märkbar blir denna acceleration. I det här avsnittet undersöker vi riktningen och storleken på den accelerationen.

Figur 1 visar ett objekt som rör sig i en cirkulär bana med konstant hastighet. Riktningen för den momentana hastigheten visas vid två punkter längs banan. Accelerationen är i riktning mot hastighetsförändringen, som pekar direkt mot rotationscentret (mitten av den cirkulära banan). Denna pekning visas med vektordiagrammet i figuren. Vi kallar accelerationen av ett objekt som rör sig i enhetlig cirkelrörelse (som härrör från en netto extern kraft) centripetalaccelerationen(ac); centripetal betyder ”mot mitten” eller ”centrumsökning.”

den givna figuren visar en cirkel, med en triangel med hörn A B C gjord från mitten till gränsen. A är i mitten och B-och C-punkterna är vid cirkelvägen. Linjerna A B och A C fungerar som radier och B C är ett ackord. Delta theta visas inuti triangeln, och båglängden delta s och ackordlängden delta r ges också. Vid punkt B visas objektets hastighet som v ett och vid punkt C visas objektets hastighet som v två. Längs cirkeln visas en ekvation som delta v är lika med v sub 2 minus v sub 1.

Figur 1. Riktningarna för hastigheten hos ett objekt vid två olika punkter visas, och förändringen i hastighet Cyrv ses att peka direkt mot krökningscentrum. (Se liten insats.) Eftersom ac = Acc / Acct är accelerationen också mot mitten; ac kallas centripetalacceleration. (Eftersom det är mycket liten, är båglängden (s) lika med ackordlängden (S) (S) för små tidsskillnader.)

riktningen för centripetalacceleration är mot krökningscentret,men vad är dess storlek? Observera att triangeln som bildas av hastighetsvektorerna och den som bildas av radierna och Uics är likartade. Både trianglarna ABC och PQR är isosceles trianglar (två lika sidor). De två lika sidorna av hastighetsvektortriangeln är hastigheterna v1 = v2 = v. Med hjälp av egenskaperna hos två liknande trianglar får vi \frac{\Delta{v}}{v}=\frac{\Delta{s}}{r}\\.

Acceleration är \frac {\Delta{v}} {\Delta{T}}\\, och så löser vi först detta uttryck för Ubicv:

\displaystyle\Delta{v}=\frac{v}{r}\Delta{s}\\.

sedan delar vi detta med Ax, vilket ger

\displaystyle\frac{\Delta{v}}{\Delta{t}}=\frac{v}{r}\times\frac{\Delta{s}}{\Delta{t}}\\.

slutligen noterar vi att \frac{\Delta{v}}{\Delta{t}}=a_c\\ och att \frac{\Delta{s}}{\Delta{T}}=v\\, den linjära eller tangentiella hastigheten, ser vi att storleken på centripetalaccelerationen är

{a}_c=\frac{v^2}{r}\\,

vilket är accelerationen av ett objekt i en cirkel med radie r vid en hastighet V. Så centripetalaccelerationen är större vid höga hastigheter och i skarpa kurvor (mindre radie), som du har märkt när du kör bil. Men det är lite förvånande att ac är proportionell mot hastigheten i kvadrat, vilket till exempel innebär att det är fyra gånger så svårt att ta en kurva vid 100 km/h än vid 50 km/h. ett skarpt hörn har en liten radie, så att ac är större för stramare varv, som du säkert har märkt.

det är också användbart att uttrycka ac när det gäller vinkelhastighet. Genom att ersätta v = rw i ovanstående uttryck hittar vi a_c=\frac{\left(r\omega\right)^2}{r}=r\omega^2\\. Vi kan uttrycka storleken på centripetal acceleration med någon av två ekvationer:

\displaystyle{a}_c=\frac{v^2}{r}; a_c=r\omega^2\\.

minns att ac-riktningen är mot mitten. Du kan använda vilket uttryck som är bekvämare, vilket illustreras i exemplen nedan.

en centrifug (se Figur 2B) är en roterande anordning som används för att separera prover med olika densiteter. Hög centripetalacceleration minskar avsevärt den tid det tar för separation att inträffa och möjliggör separation med små prover. Centrifuger används i en mängd olika tillämpningar inom vetenskap och medicin, inklusive separation av enstaka cellsuspensioner såsom bakterier, virus och blodceller från ett flytande medium och separation av makromolekyler, såsom DNA och protein, från en lösning. Centrifuger klassificeras ofta i termer av deras centripetalacceleration relativt acceleration på grund av tyngdkraften (g); maximal centripetalacceleration på flera hundra tusen g är möjlig i vakuum. Mänskliga centrifuger, extremt stora centrifuger, har använts för att testa astronauternas tolerans mot effekterna av accelerationer som är större än jordens gravitation.

exempel 1. Hur jämför centripetalaccelerationen av en bil runt en kurva med den på grund av tyngdkraften?

vad är storleken på centripetalaccelerationen för en bil efter en kurva med radie 500 m med en hastighet av 25, 0 m/s (ca 90 km/h)? Jämför accelerationen med den på grund av tyngdkraften för denna ganska mjuka kurva som tas vid motorvägshastighet. Se figur 2a.

strategi

eftersom v och r ges är det första uttrycket i \ displaystyle{a}_c= \ frac{v^2}{r}; a_c=r\omega^2\\ Det mest praktiska att använda.

lösning

Ange de angivna värdena för v = 25,0 m/S och r=500 m i det första uttrycket för ac ger

\displaystyle{a}_c=\frac{v^2}{r}=\frac{\left(25,0\text{ m/s}\right)^2}{500\text{ m}}=1,25\text{ m/s}^2\\.

diskussion

för att jämföra detta med accelerationen på grund av tyngdkraften (g = 9,80 m / s2) tar vi förhållandet mellan \displaystyle\frac{a_c}{g}=\frac{\left(1.25\text{ m / s}^2 \ höger)} {\vänster(9.80\text{ m/s}^2\höger)}=0.128\\. Således ac=0,128 g och märks särskilt om du inte hade ett säkerhetsbälte.

i Figur A körs en bil som visas uppifrån på en cirkulär väg runt en cirkulär väg. Parkens centrum kallas centrum för denna cirkel och avståndet från denna punkt till bilen tas som radie r. Den linjära hastigheten visas i vinkelrät riktning mot framsidan av bilen, visas som v centripetalaccelerationen visas med en pil riktad mot rotationscentret. I Figur b visas en centrifug ett objekt med massa m roterar i det med konstant hastighet. Objektet är på avståndet lika med radien, r, av centrifugen. Centripetalaccelerationen visas mot rotationscentret och hastigheten, v visas vinkelrätt mot objektet medurs.

Figur 2. (a) bilen som följer en cirkulär bana med konstant hastighet accelereras vinkelrätt mot dess hastighet, såsom visas. Storleken på denna centripetalacceleration finns i Exempel 1. (b) en partikel av massa i en centrifug roterar med konstant vinkelhastighet . Det måste accelereras vinkelrätt mot dess hastighet eller det skulle fortsätta i en rak linje. Storleken på den nödvändiga accelerationen finns i Exempel 2.

exempel 2. Hur stor är centripetalaccelerationen i en Ultracentrifuge?

beräkna centripetalaccelerationen för en punkt 7.50 cm från axeln av en ultracentrifuge spinning vid 7,5 ml 104 varv/min. Bestäm förhållandet mellan denna acceleration och det på grund av tyngdkraften. Se Figur 2B.

strategi

termen varv/min står för varv per minut. Genom att konvertera detta till radianer per sekund, vi får vinkelhastigheten Bisexuell. Eftersom r ges kan vi använda det andra uttrycket i ekvationen a_c=\frac{v^2}{r};a_c=r\omega^2\\ för att beräkna centripetalaccelerationen.

lösning

för att konvertera 7.50 104 varv / min till radianer per sekund använder vi fakta om att en revolution är 2 60,0 varv och en minut är 60,0 s. således

\displaystyle\omega=7.50\times10^4\frac{\text{rev}}{\text{min}}\times\frac{2\pi\text{ rad}}{1\text{ rev}} \ times \ frac{1\text{ min}}{60.0\text{ s}} = 7854\text{ rad / s}\\.

nu ges centripetalaccelerationen av det andra uttrycket i

\displaystyle{a}_c=\frac{v^2}{r}; a_c=r\omega^2\\ som ac = rw2.

konvertera 7,50 cm till meter och ersätta kända värden ger ac = (0,0750 m) (7854 rad/s)2 = 4.63 ml 106 m/s2.

Observera att de enhetslösa radianerna kasseras för att få rätt enheter för centripetalacceleration. Med förhållandet mellan ac och g ger

\frac{a_c}{g}=\frac{4.63\times10^6}{9.80}=4.72\times10^5\\.

diskussion

detta sista resultat innebär att centripetalaccelerationen är 472 000 gånger så stark som g. det är inte konstigt att sådana höga citruscentrifuger kallas ultracentrifuger. De extremt stora accelerationerna som är involverade minskar kraftigt den tid som behövs för att orsaka sedimentering av blodkroppar eller andra material.

naturligtvis behövs en netto extern kraft för att orsaka någon acceleration, precis som Newton föreslog i sin andra lag om rörelse. Så en netto extern kraft behövs för att orsaka en centripetalacceleration. I centripetalkraft kommer vi att överväga de krafter som är involverade i cirkulär rörelse.

PhET Explorations: Ladybug Motion 2D

lär dig om position, hastighet och accelerationsvektorer. Flytta nyckelpigan genom att ställa in position, hastighet eller acceleration och se hur vektorerna ändras. Välj linjär, cirkulär eller elliptisk rörelse och spela in och spela upp rörelsen för att analysera beteendet.

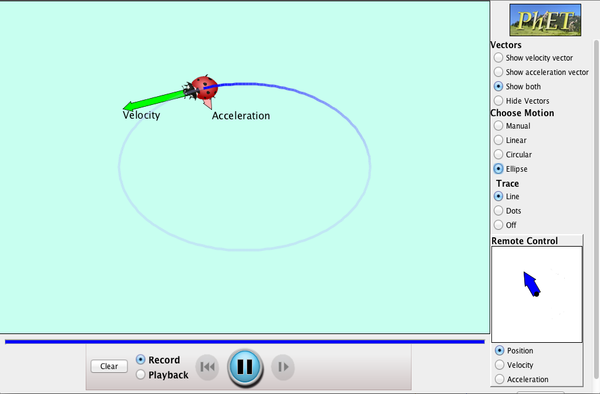
nyckelpiga Motion 2D skärmdump.

klicka på bilden för att ladda ner. Använd Java för att köra simuleringen.

avsnitt sammanfattning

  • Centripetal acceleration ac är accelerationen upplevs medan i enhetlig cirkelrörelse. Den pekar alltid mot rotationscentret. Den är vinkelrät mot den linjära hastigheten v och har storleken {a}_{\text{c}} = \frac{{v}^{2}}{r}; {a} _ {\text{c}}={\mathrm{r \ omega }}^{2}\\.
  • enheten för centripetalacceleration är m / s2.

konceptuella frågor

  1. kan centripetal acceleration ändra hastigheten på cirkulär rörelse? Förklara.

problem& övningar

  1. en nöjesfält rider sina passagerare inuti en flygande tefatformad Behållare. Om den horisontella cirkulära vägen som ryttarna följer har en radie på 8,00 m, hur många varv per minut kommer ryttarna att utsättas för en centripetalacceleration vars storlek är 1,50 gånger den på grund av tyngdkraften?
  2. en löpare som deltar i 200 m streck måste springa runt slutet av ett spår som har en cirkulär båge med en krökningsradie på 30 m. om han fullbordar 200 m streck på 23,2 s och kör med konstant hastighet under hela loppet, vad är storleken på hans centripetala acceleration när han kör den krökta delen av spåret?
  3. att ta jordens ålder för att vara ca 4 kg 109 år och antar dess omloppsradie på 1.5 1011 har inte förändrats och är cirkulär, beräkna det ungefärliga totala avståndet jorden har rest sedan dess födelse (i en referensram stationär med avseende på solen).
  4. propellern för ett andra världskrigets stridsflygplan är 2,30 m i diameter. (A) Vad är dess vinkelhastighet i radianer per sekund om den snurrar vid 1200 varv/min? (B) Vad är den linjära hastigheten på dess spets vid denna vinkelhastighet om planet står stilla på asfalten? (C) Vad är centripetalaccelerationen av propellerspetsen under dessa förhållanden? Beräkna den i meter per sekund kvadrat och konvertera till multiplar av g.
  5. en vanlig verkstadsslipsten har en radie på 7,50 cm och roterar vid 6500 varv/min. (A) beräkna storleken på centripetalaccelerationen vid dess kant i meter per sekund kvadrat och konvertera den till multiplar av g. (b) Vad är den linjära hastigheten för en punkt på dess kant?
  6. helikopterblad tål enorma påfrestningar. Förutom att stödja vikten på en helikopter snurras de i snabba hastigheter och upplever stora centripetala accelerationer, särskilt vid spetsen. (A) beräkna storleken på centripetalaccelerationen vid spetsen på ett 4,00 m långt helikopterblad som roterar med 300 varv/min. (B) jämför spetsens linjära hastighet med ljudets hastighet (tagen till 340 m/s).
  7. Olympiska skridskoåkare kan snurra vid cirka 5 varv / s. (a) Vad är deras vinkelhastighet i radianer per sekund? (B) Vad är centripetalaccelerationen för skaterens näsa om den är 0,120 m från rotationsaxeln? (c) en exceptionell åkare som heter Dick Button kunde snurra mycket snabbare på 1950—talet än någon annan sedan-ungefär 9 varv/s. Vad var centripetalaccelerationen av nässpetsen, förutsatt att den ligger vid 0,120 m radie? D) kommentera storleken på de accelerationer som hittats. Det sägs att Button bröt små blodkärl under sina snurr.
  8. vilken procentandel av accelerationen vid jordens yta är accelerationen på grund av tyngdkraften vid positionen för en satellit som ligger 300 km över jorden?
  9. verifiera att den linjära hastigheten för en ultracentrifug är cirka 0,50 km/s och jorden i dess omlopp är cirka 30 km/s genom att beräkna: (a) den linjära hastigheten för en punkt på en ultracentrifug 0.100 m från centrum, roterande vid 50 000 varv / min; (b) jordens linjära hastighet i sin omlopp om solen (använd data från texten på jordens omloppsbana och approximera den som cirkulär).
  10. en roterande rymdstation sägs skapa”artificiell gravitation” —en löst definierad term som används för en acceleration som skulle vara grovt lik gravitationen. Den roterande rymdstationens yttervägg skulle bli ett golv för astronauterna, och centripetalacceleration som levereras av golvet skulle göra det möjligt för astronauter att utöva och upprätthålla muskel-och benstyrka mer naturligt än i icke-roterande rymdmiljöer. Om rymdstationen är 200 m i diameter, vilken vinkelhastighet skulle ge en” konstgjord gravitation ” på 9, 80 m/s2 vid fälgen?
  11. vid start har en kommersiell jet en 60,0 m / s hastighet. Däcken har en diameter på 0,850 m. (a) vid hur många varv/min roterar däcken? (B) Vad är centripetalaccelerationen vid däckets kant? (c) med vilken kraft måste en bestämd 1,00 ml 10-15 kg bakterie klamra sig fast vid fälgen? (d) ta förhållandet mellan denna kraft och bakteriens vikt.
  12. integrerade koncept. Ryttare i en nöjespark rida formad som en vikingaskepp hängde från en stor pivot roteras fram och tillbaka som en styv pendel. Någon gång nära mitten av resan är fartyget tillfälligt rörligt högst upp i sin cirkulära båge. Fartyget svänger sedan ner under påverkan av tyngdkraften. (a) förutsatt försumbar friktion, hitta hastigheten på ryttarna längst ner på bågen, med tanke på systemets masscentrum färdas i en båge med en radie på 14,0 m och ryttarna är nära masscentrum. (B) Vad är centripetalaccelerationen längst ner på bågen? (C) rita ett fritt kroppsschema över de krafter som verkar på en ryttare längst ner på bågen. (D) hitta den kraft som utövas av resan på en 60,0 kg ryttare och jämföra den med hennes vikt. (e) diskutera om svaret verkar rimligt.
  13. orimliga resultat. En mamma skjuter sitt barn på en gunga så att hans hastighet är 9.00 m / s vid den lägsta punkten på hans väg. Gungan är upphängd 2,00 m över barnets masscentrum. (A) Vad är storleken på centripetalaccelerationen hos barnet vid lågpunkten? (B) Vad är storleken på den kraft som barnet utövar på sätet om hans massa är 18,0 kg? (C) Vad är orimligt med dessa resultat? D) vilka förutsättningar är orimliga eller inkonsekventa?

ordlista

centripetal acceleration: accelerationen av ett objekt som rör sig i en cirkel, riktad mot mitten

ultracentrifuge: en centrifug optimerad för att snurra en rotor vid mycket höga hastigheter

valda lösningar på problem& övningar

1. 12,9 varv/min

3. 4 kg 1021 m

5. a) 3,47 104 m/s2, 3,55 103 G.b) 51,1 m/s

7. a) 3.14 rad/s; b) 118 m/s; c)384 m/s; d) den centripetala acceleration som känns av Olympiska åkare är 12 gånger större än accelerationen på grund av tyngdkraften. Det är en hel del acceleration i sig. Centripetalaccelerationen kände av knappens näsa var 39,2 gånger större än accelerationen på grund av tyngdkraften. Det är inte konstigt att han bröt små blodkärl i sina snurr.

9. a) 0,524 km/s; b) 29,7 km/s

11. a) 1,35 ci 103 rpm; b) 8,47 ci 103 m/s2; c) 8,47 ci 10-12 n; d) 865

12. (a) 16,6 m/s; (b) 19,6 m/s2;

(c)

en rektangel med en bas längre än höjden. En vertikal linje med pilspetsar i båda ändarna passerar genom rektangeln och skär de horisontella sidorna. Pilens övre del är märkt N och botten är märkt w. ;

(d) 1,76 103 n eller 3,00 w, det vill säga den normala kraften (uppåt) är tre gånger hennes vikt; (e) detta svar verkar rimligt, eftersom hon känner att hon tvingas in i stolen mycket starkare än bara av tyngdkraften.

13. (a) 40,5 m/s2; (b) 905 N; (c) kraften delvis (b) är mycket stor. Accelerationen i del (A) är för mycket, ca 4 g; (d) svängningens hastighet är för stor. Vid den givna hastigheten längst ner på gungan finns det tillräckligt med kinetisk energi för att skicka barnet hela vägen över toppen och ignorera friktion.