regressionsanalys > Homoscedasticitet / homogenitet av varians / antagande av lika varians

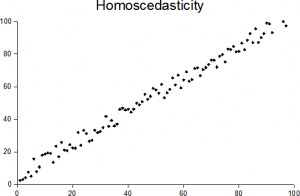
bild: sreebot| Wikimedia Commons

enkelt uttryckt betyder homoscedasticitet ”att ha samma spridning.”För att den ska existera i en uppsättning data måste punkterna vara ungefär samma avstånd från linjen, som visas på bilden ovan. Motsatsen är heteroscedasticitet (”olika scatter”), där punkter ligger på mycket varierande avstånd från regressionslinjen.

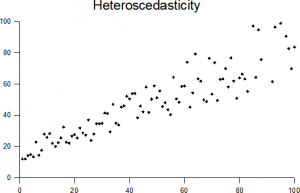
punkterna högre på x-axeln har en större varians än mindre värden.

Observera att jag sa ”avstånd” här och inte varians. När du tittar på en graf är det lättare att titta på avstånden från punkterna till linjen för att avgöra om en uppsättning data visar homoscedasticitet. Tekniskt sett är det variansen som räknas, och det är vad du skulle använda i beräkningar. Men eftersom varians kräver en formel är det omöjligt att ögongloben på en graf.

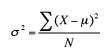
Variansformel.

eftersom variansen bara är standardavvikelsen kvadrat, kan du också se homoscedasticitet beskrivs som ett tillstånd där standardavvikelserna är lika för alla punkter.

i mer formella termer

Du kommer sällan att stöta på en uppsättning data som har en varians på noll. Du är mer benägna att se avvikelser som sträcker sig var som helst från 0.01 till 101.01. Så när klassificeras en datauppsättning som homoscedasticitet? Den allmänna tumregeln1 är:

om förhållandet mellan den största variansen och den minsta variansen är 1,5 eller under, är data homoscedastic.

Vad är antagandet om lika varians?

antagandet om lika variationer (dvs. antagandet om homoscedasticitet) förutsätter att olika prover har samma varians, även om de kom från olika populationer. Antagandet finns i många statistiska tester, inklusive variansanalys (ANOVA) och studentens T-Test. Andra tester, som Welchs T-Test, kräver inte lika stora avvikelser alls.
att köra ett test utan att kontrollera om det finns lika variationer kan ha en betydande inverkan på dina resultat och kan till och med ogiltigförklara dem helt. Hur mycket dina resultat påverkas beror på vilket test du använder och hur känsligt det testet är för ojämlika avvikelser. Till exempel, medan ett ANOVA-test med fast faktor med lika provstorlekar endast påverkas en liten mängd, kan en ANOVA med ojämna provstorlekar ge dig helt ogiltiga resultat.

antagandet om lika variationer används också i linjär regression, vilket förutsätter att data är homoscedastiska. Enkelt uttryckt, om dina data är brett spridda om (som att Kona form i den heteroscedastiska bilden ovan), kommer regression inte att fungera så bra. För mer information om detta ämne, se antaganden & villkor för Regression.

testning för homogenitet av varians

tester som du kan köra för att kontrollera dina data uppfyller detta antagande inkluderar:

• Bartletts Test
• Box ’ s m Test
• Brown-Forsythe Test
• Hartleys Fmax test
• Levenes Test

——————————————————————————

behöver du hjälp med en läxa eller testfråga? Med Chegg Study kan du få steg-för-steg-lösningar på dina frågor från en expert på området. Din första 30 minuter med en Chegg handledare är gratis!