ett alternativt normalitetstest är Shapiro-Wilk-testet.

• Vad är ett Kolmogorov-Smirnov normalitetstest?
• SPSS Kolmogorov-Smirnov test från NPAR tester
• SPSS Kolmogorov-Smirnov test från undersök variabler
• Rapportera ett Kolmogorov-Smirnov Test
• fel resultat i SPSS?

Vad är en Kolmogorov-Smirnov normalitet test?

Kolmogorov-Smirnov-testet undersöker om poäng
sannolikt kommer att följa viss fördelning i vissa populationer.För att undvika förvirring finns det 2 Kolmogorov-Smirnov-tester:

• Det finns ett prov Kolmogorov-Smirnov-test för testning om en variabel följer en given fördelning i en population. Denna ” givna distribution ”är vanligtvis-inte alltid – den normala fördelningen, därav”Kolmogorov-Smirnov normalitetstest”.
• Det finns också (mycket mindre vanliga) oberoende prover Kolmogorov-Smirnov test för testning om en variabel har identiska fördelningar i 2 populationer.

i teorin kan ”Kolmogorov-Smirnov-testet” hänvisa till antingen test (men hänvisar vanligtvis till Kolmogorov-Smirnov-testet) och hade bättre undvikits. Förresten är båda Kolmogorov-Smirnov-testerna närvarande i SPSS.

Kolmogorov-Smirnov Test-enkelt exempel

Så säg att jag har en befolkning på 1 000 000 personer. Jag tror att deras reaktionstider på någon uppgift är helt normalt fördelade. Jag prov 233 av dessa människor och mäta deras reaktionstider.
Nu kommer den observerade frekvensfördelningen av dessa troligen att skilja sig lite – men inte för mycket-från en normalfördelning. Så jag kör ett histogram över observerade reaktionstider och överlappar en normal fördelning med samma medelvärde och standardavvikelse. Resultatet visas nedan.

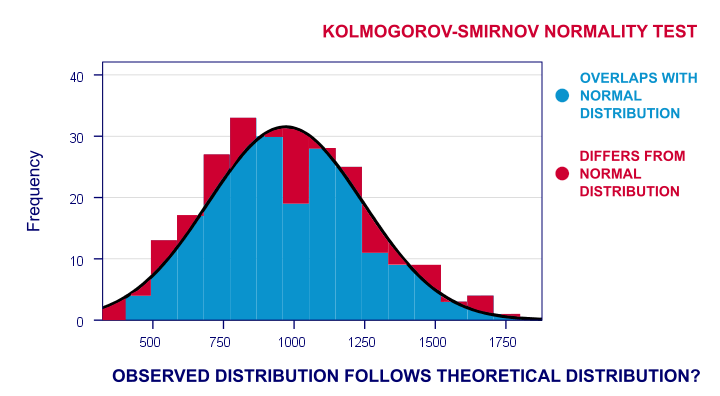
frekvensfördelningen av mina poäng överlappar inte helt med min normala kurva. Nu kunde jag beräkna andelen fall som avviker från den normala kurvan-andelen röda områden i diagrammet. Denna procentandel är en teststatistik: den uttrycker i ett enda nummer hur mycket mina data skiljer sig från min nollhypotes. Så det indikerar i vilken utsträckning de observerade poängen avviker från en normal fördelning.
Nu, om min nollhypotes är sant, bör denna avvikelseprocent förmodligen vara ganska liten. Det vill säga en liten avvikelse har ett högt sannolikhetsvärde eller p-värde.
omvänt är en enorm avvikelseprocent mycket osannolik och föreslår att mina reaktionstider inte följer en normal fördelning i hela befolkningen. Så en stor avvikelse har ett lågt p-värde. Som en tumregel, varutsätta nollhypotesen om p < 0.05.So om p < 0.05, tror vi inte att vår variabel följer en normal fördelning i vår befolkning.

Kolmogorov-Smirnov Test-teststatistik

så det är det enklaste sättet att förstå hur Kolmogorov-Smirnov normalitetstest fungerar. Beräkningsmässigt fungerar det emellertid annorlunda: det jämför de observerade kontra de förväntade kumulativa relativa frekvenserna som visas nedan.

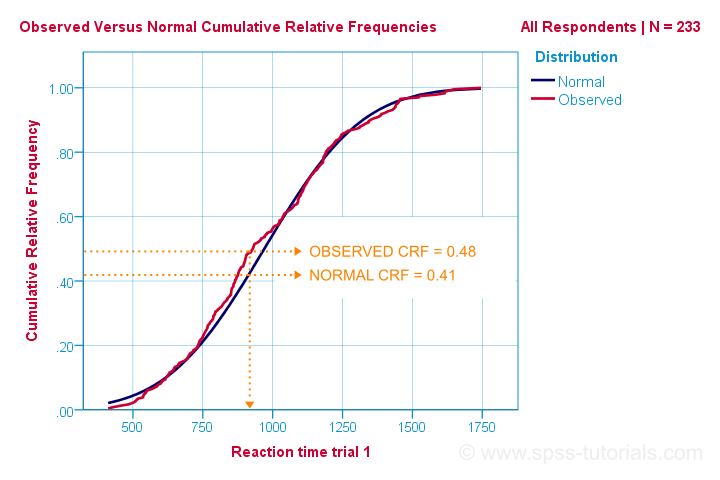
Kolmogorov – Smirnov-testet använder den maximala absoluta skillnaden mellan dessa kurvor som dess teststatistik betecknad med D. i detta diagram är den maximala absoluta skillnaden D (0,48 – 0,41 =) 0,07 och det sker vid en reaktionstid på 960 millisekunder. Tänk på att D = 0.07 som vi kommer att stöta på det i vår SPSS-utgång på en minut.

Kolmogorov-Smirnov-testet i SPSS

det finns 2 sätt att köra testet i SPSS:

• NPAR tester som finns under analysera icke-parametriska tester äldre dialoger 1-prov K-S… är vår metod för val eftersom det skapar snyggt detaljerad produktion.
• undersök variabler från analysera beskrivande statistik Utforska är ett alternativ. Detta kommando kör både Kolmogorov-Smirnov-testet och Shapiro-Wilk normalitetstest.
  Observera att undersök variabler använder listvis uteslutning av saknade värden som standard. Så om jag testar 5 variabler, använder mina 5 tester endast fall som inte har några missningar på någon av dessa 5 variabler. Detta är vanligtvis inte vad du vill men vi visar hur du undviker detta.

vi visar båda metoderna med speedtasks.sav hela, varav en del visas nedan.

vår huvudsakliga forskningsfråga ärvilken av reaktionstidsvariablerna är sannolikt
att normalt distribueras i vår befolkning?Dessa data är ett läroboksexempel på varför du bör noggrant inspektera dina data innan du börjar redigera eller analysera dem. Låt oss göra just det och köra några histogram från syntaxen nedan.

resultat

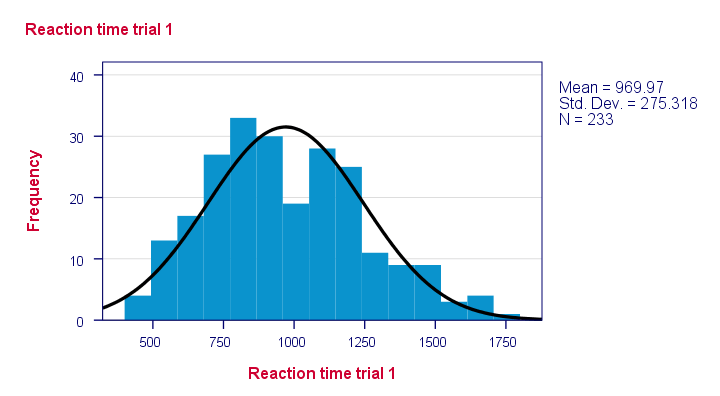
Observera att vissa distributioner inte ser trovärdiga alls. Men vilka kommer sannolikt att distribueras normalt?

SPSS Kolmogorov-Smirnov test från NPAR tester

vårt föredragna alternativ för att köra Kolmogorov-Smirnov testet är underAnalyze Nonparametric tester äldre dialoger 1-prov K-S… som visas nedan.

därefter fyller vi bara i dialogrutan som visas nedan.

klicka på Klistra resulterar i syntaxen nedan. Nu kör vi det.

Kolmogorov-Smirnov Testsyntax från icke-parametriska tester

resultat

först och främst, notera att teststatistiken för vår första variabel är 0.073-precis som vi såg i vårt kumulativa relativa frekvensdiagram lite tidigare. Diagrammet innehåller exakt samma data som vi bara körde vårt test på så dessa resultat konvergerar snyggt.
angående vår forskningsfråga: endast reaktionstiderna för försök 4 verkar vara normalt fördelade.

SPSS Kolmogorov-Smirnov test från undersök variabler

ett alternativt sätt att köra Kolmogorov-Smirnov testet startar från analysera beskrivande statistik Exploreas visas nedan.

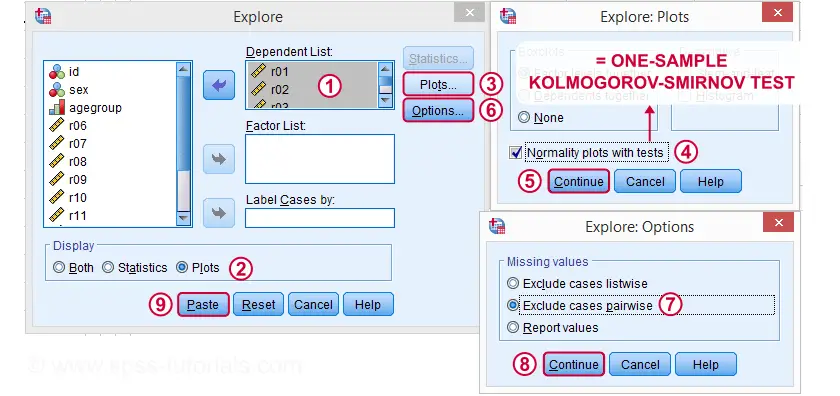
Kolmogorov – Smirnov Testsyntax från icke-parametriska tester

Results

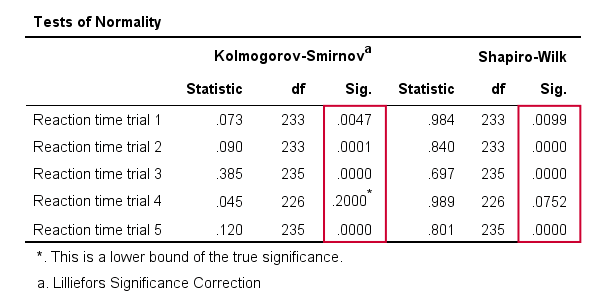
As a rule of thumb, we conclude thata variable is not normally distributed if ”Sig.” < 0.05.Så både Kolmogorov-Smirnov-testet såväl som Shapiro-Wilk-testresultaten tyder på att endast Reaktionstidsprov 4 följer en normal fördelning i hela befolkningen.
observera vidare att Kolmogorov-Smirnov-testresultaten är identiska med de som erhållits från NPAR-test.

Rapportera ett Kolmogorov-Smirnov-Test

för att rapportera våra testresultat enligt APA-riktlinjerna skriver vi något som ” ett Kolmogorov-Smirnov-test indikerar att reaktionstiderna vid försök 1 inte följer en normalfördelning, D (233) = 0,07, p = 0,005.”För ytterligare variabler, försök att förkorta detta men se till att du inkluderar

• D (för ”skillnad”), Kolmogorov-Smirnov-teststatistiken,
• df, frihetsgraderna (som är lika med N) och
• p, den statistiska betydelsen.

fel resultat i SPSS?

Om du är en student som bara vill klara ett test kan du sluta läsa nu. Följ bara stegen vi diskuterade hittills så blir du bra.

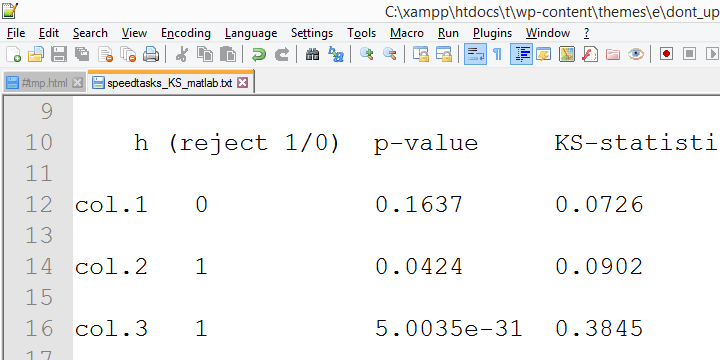
just nu, låt oss köra exakt samma tester igen i SPSS version 18 och ta en titt på utgången.

i denna utgång ingår de exakta p-värdena och-lyckligtvis – de är mycket nära de asymptotiska p-värdena. Mindre lyckligtvis är SPSS version 18-resultaten väldigt olika
från SPSS version 24 resultatvi rapporterade hittills.
anledningen verkar vara lilliefors signifikanskorrigering som tillämpas i nyare SPSS-versioner. Resultatet verkar vara att de asymptotiska signifikansnivåerna skiljer sig mycket mer från den exakta betydelsen än de gjorde när korrigeringen inte är underförstådd. Detta väcker allvarliga tvivel om riktigheten av” Lilliefors-resultaten ” – standard i nyare SPSS-versioner.
konvergerande bevis för detta förslag samlades in av min kollega Alwin Stegeman som reran alla tester i Matlab. Matlab-resultaten överensstämmer med SPSS 18-resultaten och därmed inte med de nyare resultaten.

Kolmogorov – Smirnov normalitetstest-begränsad användbarhet

Kolmogorov – Smirnov-testet är ofta att testa normalitetsantagandet som krävs av många statistiska tester som ANOVA, t-testet och många andra. Det är dock nästan rutinmässigt förbises att sådana tester är robusta mot en kränkning av detta antagande om provstorlekar är rimliga, säger n 25.Den bakomliggande orsaken till detta är central limit theorem. Därför behövs normalitetstester endast för små provstorlekarom målet är att uppfylla normalitetsantagandet.
tyvärr resulterar små provstorlekar i låg statistisk effekt för normalitetstester. Detta innebär att väsentliga avvikelser från normalitet inte kommer att leda till statistisk signifikans. Testet säger att det inte finns någon avvikelse från normalitet medan det faktiskt är enormt. Kort sagt, situationen där normalitetstester behövs – små provstorlekar-är också den situation där de presterar dåligt.

Tack för att du läste.