In Bezug auf die Zuverlässigkeit bedeutet parallel, dass jedes der Elemente in der parallelen Struktur das Funktionieren des Systems ermöglicht. Dies bedeutet nicht, dass sie physikalisch parallel sind (in allen Fällen), da parallele Kondensatoren ein bestimmtes Verhalten in der Schaltung bereitstellen und wenn ein Kondensator ausfällt, kann dieses System ausfallen.
In dieser einfachen Zeichnung gibt es n Komponenten parallel und jede Komponente wird benötigt, damit das System funktioniert.

Wenn Komponente #2 ausfällt, erlauben die anderen, dass das System funktioniert.

Einfach. Und, sehr nützlich. Diese Konstruktion erlaubt die Verbesserung der Zuverlässigkeit insgesamt, sogar über die Zuverlässigkeit der einzelnen Komponenten hinaus. Im Gegensatz zu Seriensystemen, bei denen die schwächste Komponente die Zuverlässigkeit einschränkt, verbessert sich hier durch Hinzufügen von Redundanz die Systemzuverlässigkeit.

Betrachten Sie ein Zweikomponenten-Parallelsystem. Wenn beide Komponenten funktionieren, funktioniert das System. Wenn Komponente 1 oder 2 ausfällt, funktioniert das System weiterhin. Wenn und nur wenn beide Komponenten ausfallen, fällt das System aus. Im Gegensatz zu einem Seriensystem, bei dem ein Fehler einen Systemausfall verursacht, müssen in diesem einfachen Beispiel zwei Fehlerereignisse auftreten, bevor das System ausfällt.

Wie hoch ist die Wahrscheinlichkeit, dass zwei Fehler auftreten? Die Formel basiert auf der Wahrscheinlichkeit des Betriebs von Komponente 1 oder Komponente 2. Ohne die Ableitung können wir die Zuverlässigkeit des 2-Komponenten-Parallelsystems wie folgt schreiben:

Dies wird schnell sehr kompliziert mit mehr als drei Komponenten parallel. Bevor eine andere Möglichkeit zur Berechnung paralleler Systeme untersucht wird, ist zunächst eine Sonderfallsituation zu erwähnen.

Wenn die Komponenten parallel gleich sind (in Bezug auf die Zuverlässigkeit), vereinfacht sich das Obige auf

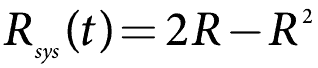
Was offensichtlich sein sollte.

Oft ist es einfacher, parallele Systemberechnungen mit der Unzuverlässigkeit oder 1 – R(t) durchzuführen. Dies ist auch die CDF oder F (t). Die Mathematik ist jetzt eher wie ein Seriensystem mit einer Korrektur. Für den allgemeinen Fall lautet die Systemzuverlässigkeitsformel für ein paralleles System

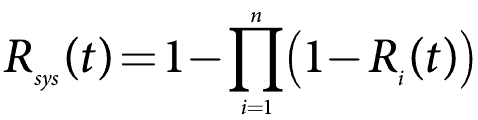
Nehmen wir also an, wir haben fünf Komponenten mit Zuverlässigkeit nach einem Jahr Nutzung, R(1), bei 90% oder 0,9. Berechnen Sie die Systemzuverlässigkeit.

Wenn wir die obige Formel verwenden und die Zuverlässigkeit jedes Elements auf 0,9 einstellen, finden wir

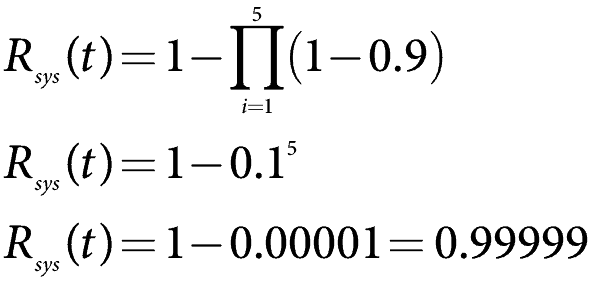
was sehr zuverlässig ist.

Es ist teuer, redundante Teile zu einem System hinzuzufügen, aber in einigen Fällen ist es die richtige Lösung, um ein System zu erstellen, das die Zuverlässigkeitsanforderungen erfüllt. Natürlich haben tatsächliche Systeme viele Variationen und Komplikationen gegenüber dem einfachen parallelen Einrichten von Komponenten. Lastverteilung, Hot-, Warm- oder Cold-Standby, Schalt- oder Abstimmungssysteme und viele andere können den Aufbau eines parallelen Systems erschweren.

Die parallele Verwendung von Komponenten ist die einzige Möglichkeit, die Systemzuverlässigkeit über die Grenzen der Zuverlässigkeit einzelner Komponenten hinaus zu erhöhen.

Verwandt:

Zuverlässigkeitsblockdiagramme Übersicht und Wert (Artikel)

Zuverlässigkeitsaufteilung (Artikel)

k aus n (Artikel)