Los ingresos son la cantidad de dinero que aporta una empresa. En este caso, los ingresos se pueden encontrar multiplicando el precio por suscripción por el número de suscriptores, o cantidad. Podemos introducir variables, p para precio por suscripción y Q para cantidad, dándonos la ecuación \text {Ingresos} = pQ.

Debido a que el número de suscriptores cambia con el precio, necesitamos encontrar una relación entre las variables. Sabemos que actualmente p = 30 y Q = 84.000. También sabemos que si el precio sube a $32, el periódico perdería de 5.000 suscriptores, dando un segundo par de valores, p=32 y Q=79,000. A partir de esto podemos encontrar una ecuación lineal que relaciona las dos cantidades. La pendiente será

\begin{align}m&=\dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{y 5,000}{2} \\ &=-2,500 \end{align}

Esto nos dice que el papel se va a perder de 2.500 suscriptores por cada dólar que subir el precio. Entonces podemos resolver para la intercepción en y.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\text{Revenue}=pQ \\ &\text{Revenue}=p\left(-2.500 p+159.000\right) \\ &\text{Revenue}=-2,500{p}^{2}+159,000 p \end{align}

Ahora tenemos una función cuadrática para los ingresos en función del cargo de suscripción. Para encontrar el precio que maximizará los ingresos para el periódico, podemos encontrar el vértice.

\begin{align}h&=-\dfrac{159,000}{2\left(-2,500\right)} \\ & =31.8 \ end{align}

El modelo nos dice que el ingreso máximo se producirá si el periódico cobra $31.80 por una suscripción. Para encontrar cuál es el máximo de ingresos, evaluamos la función de ingresos.

\begin{align}\text{ingresos máximos}&=-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right) \\ &=\2 2,528,100\hfill \end{align}

Análisis de la solución

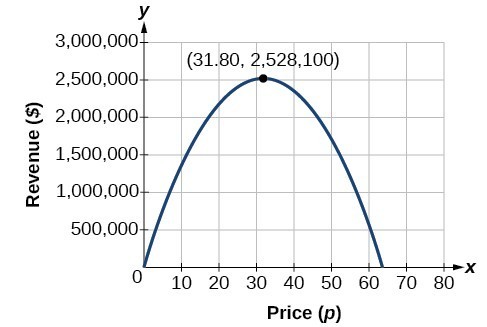
Esto también se puede resolver graficando la cuadrática. Podemos ver el ingreso máximo en un gráfico de la función cuadrática.