Revenue on yrityksen tuoma rahamäärä. Tällöin tuotto saadaan kertomalla tilauskohtainen hinta kertaamalla tilaajamäärä eli määrä. Voimme ottaa käyttöön muuttujat, P tilauksen hinnan ja Q määrän, jolloin saamme yhtälön \text{Revenue}=pQ.

koska tilaajamäärä muuttuu hinnan mukana, täytyy muuttujien välille löytää suhde. Tiedämme, että tällä hetkellä p=30 ja Q=84000. Tiedämme myös, että jos hinta nousee 32 dollariin, lehti menettäisi 5 000 tilaajaa, jolloin toinen arvopari, p=32 ja Q=79 000. Tästä voimme löytää lineaarinen yhtälö, joka liittyy kaksi suuretta. Kaltevuus on

\begin{align}m& = \dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2} \\ &=-2,500 \end{align}

Tämä kertoo, että lehti menettää 2,500 tilaajaa jokaisesta dollarista, jonka he nostavat hintaa. Voimme ratkaista y-sieppauksen.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\text{Revenue}=pq \ \ &\text{Revenue}=p\left(-2 500 p+159 000\right) \ \ &\text{revenue}=-2,500{P}^{2}+159,000 P \end{align}

meillä on nyt tilausmaksun funktiona tulojen neliöfunktio. Löytää hinta, joka maksimoi tulot sanomalehden, voimme löytää huippupiste.

\begin{align}h&=-\dfrac{159,000}{2\left(-2,500\right)} \\ &=31.8 \end{align}

malli kertoo, että maksimituotto syntyy, jos lehti veloittaa 31,80 dollaria tilauksesta. Selvittääksemme, mikä on maksimitulo, arvioimme tulofunktiota.

\begin{align}\text{maximum revenue}&=-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right) \\ &=\$2,528,100\hfill \end{align}

ratkaisun analysointi

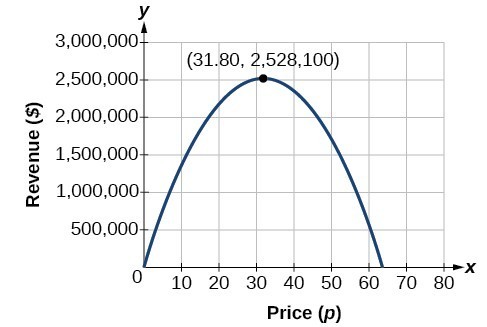
tämäkin voitaisiin ratkaista piirtämällä neliö. Voimme nähdä suurimman tulot kuvaajan, quadratic funktio.