bevétel az összeget a cég hozza. Ebben az esetben a bevétel az előfizetésenkénti ár szorozva az előfizetők számával vagy mennyiségével. Bevezethetünk változókat, p-t előfizetésenként, Q-t pedig mennyiségenként, megadva nekünk a \text{Revenue} = PQ egyenletet.

mivel az előfizetők száma az árral változik, kapcsolatot kell találnunk a változók között. Tudjuk, hogy jelenleg P = 30 és Q = 84,000. Azt is tudjuk, hogy ha az ár emelkedik $32, Az újság veszítene 5,000 előfizetők, így egy második pár értékek, p = 32 és Q=79,000. Ebből a két mennyiségre vonatkozó lineáris egyenletet találunk. A meredekség

\begin{align}m&= \ dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2} \\ &=-2,500 \end{align}

Ez azt jelzi, hogy a papír elveszíti 2,500 előfizetők minden egyes dollár emelik az árat. Ezután megoldhatjuk az y-elfogást.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\text{Revenue}=PQ \\ &\text{Revenue}=p\left(-2,500 p+159,00\right) \\ &\text{revenue}=-2,500{p}^{2}+159,000 p \end{align}

most van egy kvadratikus funkció a bevételre, mint az előfizetési díj függvénye. Ahhoz, hogy megtaláljuk az árat, amely maximalizálja az újság bevételeit, megtaláljuk a csúcsot.

\begin{align}h&=-\dfrac{159,000}{2\left(-2,500\right)} \\ &=31.8 \end{align}

A modell azt mondja, hogy a maximális bevétel akkor fordul elő, ha az újság díjak $31.80 egy előfizetés. Annak megállapításához, hogy mi a maximális bevétel, értékeljük a bevételi funkciót.

\begin{align}\text{maximum revenue}&=-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right) \\ &=\$2,528,100\hfill \end{align}

a megoldás elemzése

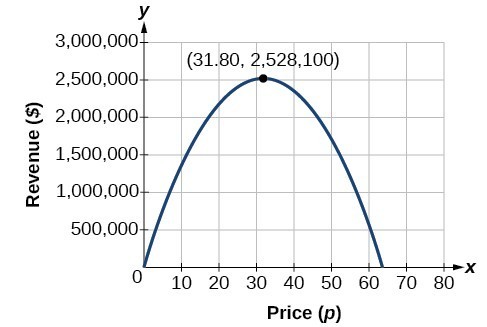
Ez a kvadratikus ábrázolásával is megoldható. A maximális bevételt a kvadratikus függvény grafikonján láthatjuk.