a megbízhatóság szempontjából a párhuzamos szerkezet bármely eleme lehetővé teszi a rendszer működését. Ez nem jelenti azt, hogy fizikailag párhuzamosak (minden esetben), mivel a kondenzátorok párhuzamosan specifikus viselkedést biztosítanak az áramkörben, és ha egy kondenzátor meghibásodik, akkor a rendszer meghibásodhat.
ebben az egyszerű rajzban n komponensek vannak párhuzamosan, és bármelyik komponensre szükség van a rendszer működéséhez.

Ha a 2. komponens meghibásodik, a többiek lehetővé teszik a rendszer működését.

egyszerű. És nagyon hasznos. Ez az építkezés lehetővé teszi a megbízhatóság javulását, még az egyes alkatrészek megbízhatósága felett is. Ellentétben a sorozatrendszerrel, ahol a leggyengébb komponens korlátozza a megbízhatóságot, itt redundancia hozzáadásával javul a rendszer megbízhatósága.

Vegyünk egy kétkomponensű párhuzamos rendszert. Ha mindkét komponens működik, akkor a rendszer működik. Ha az 1.vagy a 2. komponens meghibásodik, a rendszer továbbra is működik. Ha csak akkor, ha mindkét alkatrész meghibásodik, akkor a rendszer meghibásodik. Ellentétben egy sorozatrendszerrel, ahol bármelyik hiba rendszerhibát okoz, ebben az egyszerű példában két hibaeseménynek kell bekövetkeznie, mielőtt a rendszer meghibásodik.

mi az esélye annak, hogy két hiba van? A képlet az 1. komponens vagy a 2. komponens működési valószínűségén alapul. Anélkül, hogy a levezetése, tudjuk írni, a megbízhatóság, a 2 komponens párhuzamos rendszer:

Ez nagyon bonyolult, gyorsan, több mint három összetevő párhuzamosan. Mielőtt megvizsgálnánk a párhuzamos rendszerek kiszámításának másik módját, először meg kell említeni egy speciális esethelyzetet.

Ha az összetevők párhuzamosan azonosak (megbízhatósági szempontból), akkor a fenti egyszerűsíti

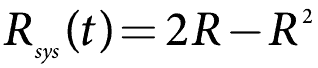
ami nyilvánvaló.

gyakran könnyebb párhuzamos rendszerszámításokat végezni a megbízhatatlanság vagy az 1 – R(t) segítségével. Ez is a CDF vagy F (t). A matematika most több, mint egy sorozat rendszer egy korrekció. Általános esetben a párhuzamos rendszer rendszer megbízhatósági képlete

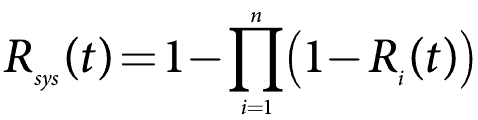
tehát öt komponensünk van megbízhatósággal egy év használat során, R(1), 90% – on vagy 0,9. Számítsa ki a rendszer megbízhatóságát.

a fenti képlettel és az egyes elemek megbízhatóságának 0,9-es beállításával

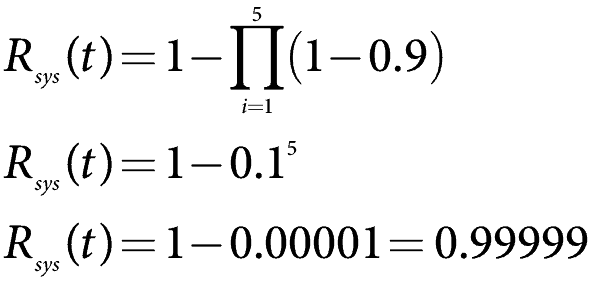
ami nagyon megbízható.

drága a redundáns alkatrészek hozzáadása a rendszerhez, de bizonyos esetekben ez a megfelelő megoldás egy olyan rendszer létrehozására, amely megfelel a megbízhatósági követelményeknek. Természetesen a tényleges rendszereknek sok variációja és komplikációja van az összetevők párhuzamos beállításával szemben. Terhelésmegosztás, meleg, meleg vagy hideg készenléti, kapcsolási vagy szavazási rendszerek, és sokan mások bonyolíthatják egy párhuzamos rendszer felépítését.

az összetevők párhuzamos használata az egyetlen módja annak, hogy növelje a rendszer megbízhatóságát az egyes komponensek megbízhatóságának határain.

kapcsolódó:

megbízhatósági blokkdiagramok áttekintése és értéke (cikk)

megbízhatósági felosztás (cikk)

n (cikk)