Entrate è la quantità di denaro che una società porta in. In questo caso, le entrate possono essere trovate moltiplicando il prezzo per abbonamento per il numero di abbonati o la quantità. Possiamo introdurre variabili, p per prezzo per abbonamento e Q per quantità, dandoci l’equazione \ text{Revenue} = pQ.

Poiché il numero di abbonati cambia con il prezzo, dobbiamo trovare una relazione tra le variabili. Sappiamo che attualmente p = 30 e Q = 84.000. Sappiamo anche che se il prezzo sale a $32, il giornale perderebbe 5.000 abbonati, dando una seconda coppia di valori, p = 32 e Q=79.000. Da questo possiamo trovare un’equazione lineare che mette in relazione le due quantità. La pendenza

\begin{align}m&=\dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2} \\ &=-2,500 \end{align}

Questo ci dice la carta perde di 2.500 iscritti per ogni dollaro che alza il prezzo. Possiamo quindi risolvere l’intercettazione Y.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\text{Revenue}=pQ \\ &\text{Revenue}=p\left(-2,500 p+159,000\right) \\ &\text{Revenue}=-2,500{p}^{2}+159,000 p \end{align}

ora Abbiamo una funzione quadratica per il fatturato, in funzione del canone di abbonamento. Per trovare il prezzo che massimizzerà le entrate per il giornale, possiamo trovare il vertice.

\begin{align}h&=-\dfrac{159,000}{2\left(-2,500\right)} \\ &=31.8 \ end {align}

Il modello ci dice che le entrate massime si verificheranno se il giornale addebita $31.80 per un abbonamento. Per trovare qual è il reddito massimo, valutiamo la funzione entrate.

\begin{align}\text{massimo di entrate}&=-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right) \\ &=\$2,528,100\hfill \end{align}

l’Analisi della Soluzione

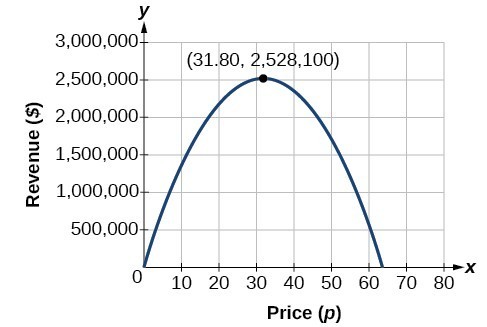
Questo potrebbe anche essere risolto con grafica quadratica. Possiamo vedere le entrate massime su un grafico della funzione quadratica.