Parlando in termini di affidabilità, parallelo, indica uno qualsiasi degli elementi nella struttura parallela che consente al sistema di funzionare. Ciò non significa che siano fisicamente paralleli (in tutti i casi), poiché i condensatori in parallelo forniscono un comportamento specifico nel circuito e se un condensatore fallisce, il sistema potrebbe fallire.
In questo semplice disegno, ci sono n componenti in parallelo e qualsiasi componente è necessario per il funzionamento del sistema.

Se il componente #2 fallisce, gli altri consentiranno al sistema di funzionare.

Semplice. E, molto utile. Questa costruzione permette il miglioramento dell’affidabilità complessiva, anche al di sopra dell’affidabilità dei singoli componenti. A differenza del sistema di serie in cui il componente più debole limita l’affidabilità, qui aggiungendo ridondanza l’affidabilità del sistema migliora.

Si consideri un sistema parallelo a due componenti. Se entrambi i componenti funzionano entrambi, il sistema funziona. Se uno dei componenti 1 o 2 fallisce, il sistema funziona ancora. Se e solo se entrambi i componenti falliscono, il sistema fallisce. A differenza di un sistema in serie in cui qualsiasi errore causa un errore di sistema, in questo semplice esempio, devono verificarsi due eventi di errore prima che il sistema fallisca.

Qual è la possibilità di avere due fallimenti? La formula si basa sulla probabilità di funzionamento del componente 1 o del componente 2. Senza fare la derivazione, possiamo scrivere l’affidabilità del sistema parallelo a 2 componenti come:

Questo diventa molto complicato rapidamente con più di tre componenti in parallelo. Prima di esplorare un altro modo per calcolare i sistemi paralleli, c’è una situazione di caso speciale da menzionare per prima.

Quando i componenti in parallelo sono gli stessi (in termini di affidabilità), quanto sopra semplifica

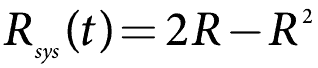
Che dovrebbe essere ovvio.

Spesso è più facile eseguire calcoli di sistema paralleli utilizzando l’inaffidabilità o 1 – R(t). Questo è anche il CDF o F (t). La matematica è ora più simile a un sistema di serie con una correzione. Per il caso generale, l’affidabilità del sistema formula per un sistema parallelo diventa

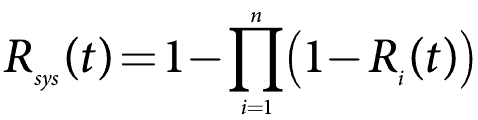
Quindi, diciamo che abbiamo cinque componenti con Affidabilità a un anno di utilizzo, R(1), al 90%, o 0.9. Calcola l’affidabilità del sistema.

Utilizzando la formula di cui sopra e impostando l’affidabilità di ciascun elemento a 0.9, troviamo

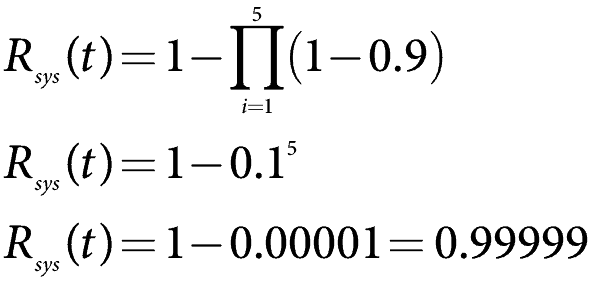
che è molto affidabile.

È costoso aggiungere parti ridondanti a un sistema, ma in alcuni casi è la soluzione giusta per creare un sistema che soddisfi i requisiti di affidabilità. Naturalmente, i sistemi attuali hanno molte varianti e complicazioni rispetto alla semplice impostazione dei componenti in parallelo. Condivisione del carico, caldo, caldo o freddo standby, commutazione o sistemi di voto, e molti altri possono complicare la costruzione di un sistema parallelo.

L’utilizzo di componenti in parallelo è l’unico modo per aumentare l’affidabilità del sistema oltre i limiti dell’affidabilità dei singoli componenti.

Correlati:

Panoramica e valore dei diagrammi a blocchi di affidabilità (articolo)

Ripartizione dell’affidabilità (articolo)

k out of n (articolo)