Articles

Abstract data structures

by admin

Abstract data types

i informatikk er en abstrakt datatype (adt) en matematisk modell for datatyper der en datatype er definert av dens oppførsel (semantikk) fra en rekke andre datatyper.synspunktet Til En Bruker av dataene, Spesielt når det gjelder mulige verdier, mulige operasjoner på data av denne typen og oppførselen til disse operasjonene. Dette står i kontrast til datastrukturer, som er konkrete representasjoner av data, og er synspunktet til en implementerer, ikke en bruker.Formelt kan EN ADT defineres som en «klasse av objekter hvis logiske oppførsel er definert av et sett med verdier og et sett med operasjoner»; dette er analogt med en algebraisk struktur i matematikk. Hva menes med «oppførsel» varierer etter forfatter, med de to hovedtyper av formelle spesifikasjoner for atferd som aksiomatisk (algebraisk) spesifikasjon og en abstrakt modell; disse tilsvarer aksiomatisk semantikk og operativ semantikk av en abstrakt maskin, henholdsvis. Noen forfattere inkluderer også beregningskompleksiteten («kostnad»), både når det gjelder tid (for databehandling) og rom (for å representere verdier).grunnen til at vi bruker abstrakte strukturer er fordi de effektivt bruker minne basert på utformingen av dataene som er lagret i dem. Med svært store mengder data eller svært ofte skiftende data, kan datastrukturen gjøre en stor forskjell i effektiviteten (kjøretid) av dataprogrammet ditt. i mer vanlig språk er en abstrakt datastruktur bare noe arrangement av data som vi har bygget inn i et ordnet arrangement.

en perfekt nydelig oversikt

noen typer abstrakte datastrukturer

Vurdert av IB

  1. statisk og dynamisk datastruktur
  • matriser
  • todimensjonale matriser
  • stabel
  • kø
  • koblet liste
  • tre
  • binær tre
  • Samlinger
  • rekursjon

    • ikke vurdert av ib, men du BØR KJENNE dem

    1. lister
    2. ordbøker
    3. sett
    4. tuppel

    grunnleggende operasjoner av datastrukturer

    jeg fant dette utmerkede lysbildet fra simon allardice.

    Grunnleggende operasjoner av matriser.png

    Sammenligning av forskjellige datastrukturer

    Datastruktur Styrker Svakheter
    matriser Sette Inn og slette – spesielt hvis du setter inn og slette i begynnelsen eller slutten av matrisen
    koblet liste direkte indeksering, lett å lage Og Bruke Direkte tilgang, søk og sortering
    stabel og kø binært tre hastighet for innsetting og sletting, tilgangshastighet, opprettholdelse av sortert rekkefølge noen overhead

    • faste strukturer er raskere/mindre
    • når du vurderer om du skal bruke en abstrakt datastruktur, bør du spørre deg selv: hva inneholder mest data og hva inneholder de mest endrede dataene?

    Sammenligning av statiske vs dynamiske datastrukturer

    denne sammenligningen brukes fra vår datavitenskap lærebok.

    Statisk datastruktur Dynamisk datastruktur
    Ineffektivt ettersom minne tildeles som kanskje ikke er nødvendig. Effektiv som mengden minne varierer etter behov.
    Rask tilgang til hvert element av data som minnestedet er løst når programmet er skrevet. Tregere tilgang til hvert element ettersom minneplasseringen tildeles under kjøring.
    minneadresser tildelt vil være sammenhengende så raskere å få tilgang. minneadresser tildelt kan være fragmentert så tregere å få tilgang.
    Strukturer er en fast størrelse, noe som gjør Dem mer forutsigbare å jobbe med. For eksempel kan de inneholde en overskrift.Strukturer varierer i størrelse, så det må være en mekanisme for å vite størrelsen på den nåværende strukturen.
    forholdet mellom ulike dataelementer endres ikke. forholdet mellom ulike dataelementer vil endres når programmet kjøres.

    Velge hvilken datastruktur å bruke

    denne grafikken brukes med enorm takknemlighet fra Dartford Grammar School Computer Science Department.

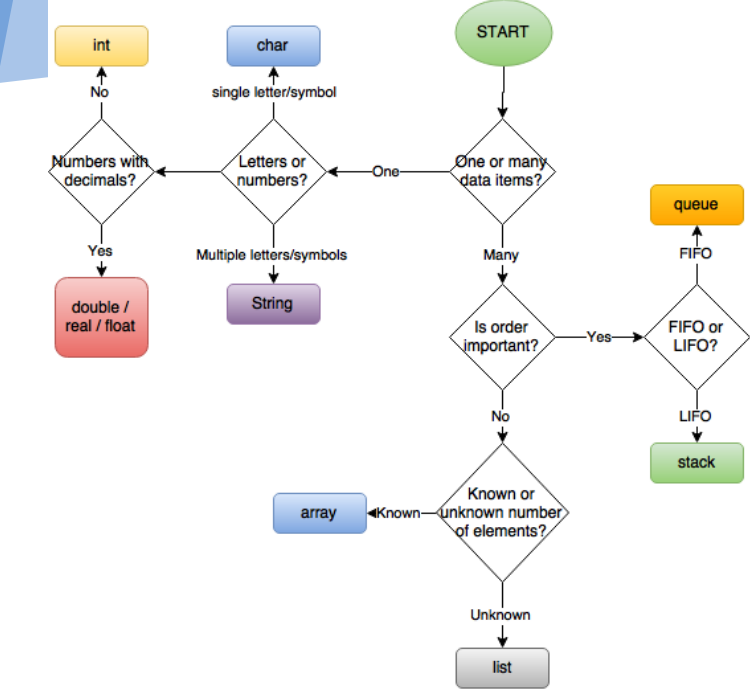
    Velge et flytskjema for datatype.png

    Standarder

    • Identifiser en situasjon som krever bruk av rekursiv tenkning.
    • Identifiser rekursiv tenkning i en spesifisert problemløsning.Spor en rekursiv algoritme for å uttrykke en løsning på et problem.
    • Beskriv egenskapene til en todimensjonal matrise.
    • Konstruer algoritmer ved hjelp av todimensjonale arrays.
    • Beskriv egenskapene og anvendelsene til en stabel.
    • Konstruer algoritmer ved hjelp av tilgangsmetodene til en stabel.
    • Beskriv egenskapene og anvendelsene til en kø.
    • Konstruer algoritmer ved hjelp av tilgangsmetodene til en kø.
    • Forklar bruken av matriser som statiske stabler og køer.
    • Beskriv funksjonene og egenskapene til en dynamisk datastruktur.
    • Beskriv hvordan koblede lister fungerer logisk.
    • Skisse lenkede lister(enkel, dobbel og sirkulær).
    • Beskriv egenskapene og anvendelsene til en samling.
    • Konstruer algoritmer ved hjelp av tilgangsmetodene til en samling.
    • Diskuter behovet for delprogrammer og samlinger innenfor programmerte løsninger.
    • Konstruer algoritmer ved hjelp av forhåndsdefinerte delprogrammer, endimensjonale matriser og / eller samlinger.
    • Beskriv hvordan trær fungerer logisk (både binært og ikke-binært).
    • Definer vilkårene: foreldre, venstre-barn, høyre-barn, undertre, rot og blad.
    • Angi resultatet av inorder, postorder og preorder tre traversering.
    • Skisse binære trær.
    • Definerer begrepet dynamisk datastruktur.
    • Sammenlign bruken av statiske og dynamiske datastrukturer.
    • Foreslå en egnet struktur for en gitt situasjon.