Inntekter er hvor mye penger et selskap bringer inn. I dette tilfellet kan inntektene bli funnet ved å multiplisere prisen per abonnement ganger antall abonnenter eller kvantitet. Vi kan introdusere variabler, p for pris per abonnement Og Q for kvantitet, noe som gir oss ligningen \ text{Revenue}=pQ.

Fordi antall abonnenter endres med prisen, må vi finne et forhold mellom variablene. Vi vet at p=30 Og Q = 84 000. Vi vet også at hvis prisen stiger til $32, vil avisen miste 5000 abonnenter, noe som gir et andre par verdier, p=32 Og Q=79.000. Fra dette kan vi finne en lineær ligning knyttet til de to mengdene. Hellingen vil være

\ beginno {align}m &=\dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2} \ \ &=-2,500 \ end{align}

dette forteller oss at papiret vil miste 2500 abonnenter for hver dollar de øker prisen. Vi kan da løse for y-avskjæringen.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\tekst{Revenue}=pQ \\ &\tekst{Revenue}=p\venstre(-2,500 p+159,000\høyre) \\ &\text{revenue}=-2,500{p}^{2}+159,000 p \end{align}

Vi har nå en kvadratisk funksjon for inntekter som en funksjon av abonnementsavgiften. For å finne prisen som vil maksimere inntektene for avisen, kan vi finne toppunktet.

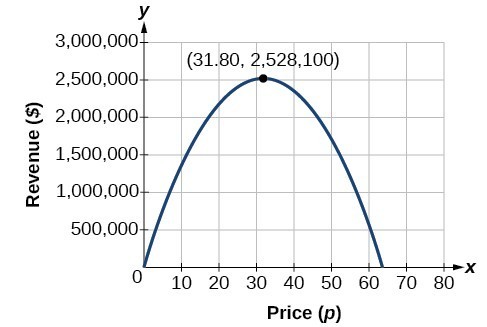
\begin{align}h &=- \ dfrac{159,000}{2 \ venstre (-2,500 \ høyre)} \ \ &=31.8 \ end{align}

modellen forteller oss at maksimal inntekt vil oppstå hvis avisen belaster $ 31,80 for et abonnement. For å finne ut hva maksimal inntekt er, vurderer vi inntektsfunksjonen.

\begin{align}\text{maksimal inntekt}&=-2,500{\venstre(31.8\høyre)}^{2}+159,000\venstre(31.8\høyre) \\ &=\$2,528,100\hfill \end{align}

analyse av løsningen

dette kan også løses ved å tegne kvadratisk. Vi kan se maksimal inntekt på en graf av den kvadratiske funksjonen.