den vanlige notasjonen til en funksjon er vanligvis skrevet som,

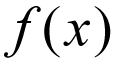
div ikke tenk på dette for bokstavelig, Det vil si at F blir multiplisert til x. I stedet anser dette som et matematisk uttrykk som leses som

ELLER

funksjoner kan også skrives på forskjellige måter ved hjelp av andre variabler som

• g(x), h(x) og k(x)

i tillegg kan funksjoner ta f(a), h(r) og k(m)

nøkkelideen er alltid å huske at variabelen utenfor parentesen er «navnet» på funksjonen, mens variabelen inne i parentesen er inngangen.verdien av funksjonen.

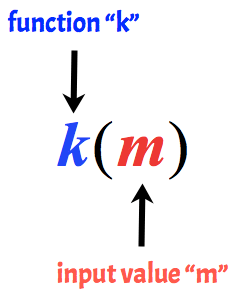
for eksempel kalles følgende funksjon k med en inngangsverdi på m.

Grunnleggende Eksempler På Evalueringsfunksjoner

Eksempel 1: Evaluer funksjonen .

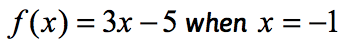
dette er den normale notasjonen av funksjonen der funksjonen er f mens inngangsverdien er x. for å evaluere en funksjon, er det vi ønsker å erstatte hver forekomst av x i uttrykket og deretter forenkle.

siden x = – 1 erstatter vi denne verdien i funksjonen og forenkler. Ved å gjøre det får vi en løsning som ser slik ut.

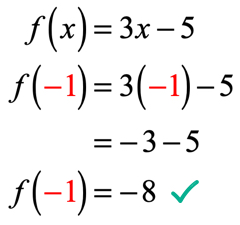
Eksempel 2: Evaluer funksjonen .

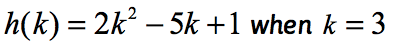
Vær oppmerksom på at funksjonen her er h og inngangsverdien er k. På samme måte som i vårt forrige eksempel, vil vi erstatte hva den numeriske verdien som er tildelt k til den gitte funksjonen, og forenkle.

siden k = 3, bør løsningen din se ut som denne

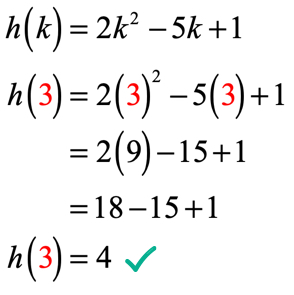
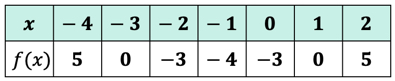
Eksempel 3: Evaluer hver verdi av x i tabellen nedenfor ved hjelp av funksjonen nedenfor. Plott punktene i xy-aksen og koble prikkene for å avsløre grafen til funksjonen.

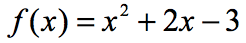
siden det er syv x-innganger, betyr det at vi også vil evaluere funksjonen syv ganger. Prøv å jobbe dette ut på egen hånd, så kom tilbake for å sjekke svarene dine.

hvis du har gjort det riktig, er disse verdiene:

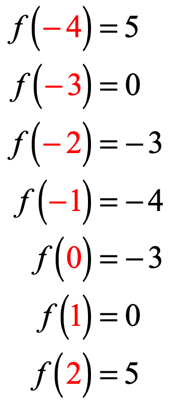
vi kan nå plassere disse utgangsverdiene i tabellen.

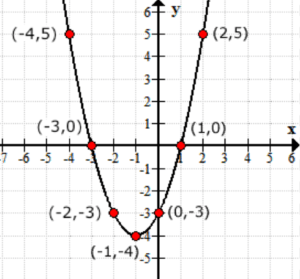
Tenk på utgangsverdiene til funksjonen f\venstre (x \ høyre) som y-verdiene. Slik ser grafen ut på xy-aksen.

Mellomliggende Eksempler På Evalueringsfunksjoner

Eksempel 4: Gitt at g\left( x \right) = {x^2} – 3x + 1, finn g\left( {2x – 1} \right).

i tidligere eksempler har vi vurdert en funksjon med et tall. Denne gangen er inngangsverdien ikke lenger en fast numerisk verdi, men i stedet et uttrykk. Det kan se komplisert ut, men prosedyren forblir den samme.

vi erstatter hver forekomst av x i g\venstre( x \høyre) med inngangsverdien som er 2x – 1. Forenkle ved å kvadrere binomial, bruke distribusjonsegenskapen og kombinere like vilkår.

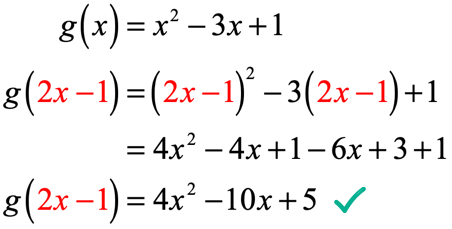
eksempel 5: gitt at p\venstre( x \høyre) = {{4x – 1} \over x} , evaluer p\venstre( 1 \høyre) – p\venstre( { – 1} \høyre).Problemet kan se skremmende ut i begynnelsen, men når vi analyserer det og bruker det vi allerede vet om hvordan vi skal evaluere funksjoner, bør dette ikke være så ille!

det vi trenger å gjøre her er å evaluere funksjonen ved x = 1 og deretter trekke av verdien av funksjonen når den evalueres ved x= -\, 1.

Vær veldig forsiktig når du erstatter verdiene og under forenklingsprosessen. Hvis du ikke er forsiktig i hvert trinn, er det veldig enkelt å begå feil når du legger til, trekker fra, multipliserer eller deler positive og negative tall.

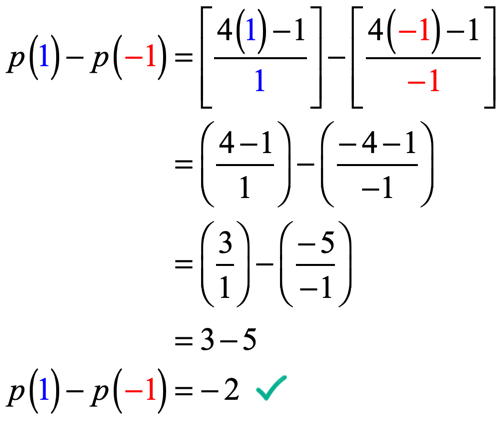
Avansert Eksempel På Å Anvende Begrepet Evalueringsfunksjoner

Eksempel 6: hvis f\left (2 \right) = 9, finn verdien av a i funksjonen nedenfor.

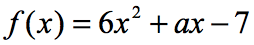
i ligningen, f\venstre( 2 \høyre) = 9, blir vi fortalt at hvis inngangen til funksjonen er 2; utgangen av funksjonen vil være 9. Siden funksjonen er gitt til oss, er vårt første trekk å i det minste erstatte verdien av 2 og deretter forenkle. Dette er hva vi får.

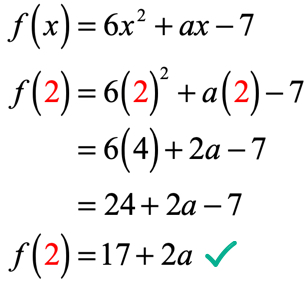
utgangen av funksjonen etter evaluering ved x = 2 er 17 + 2a. Husk, vi blir også fortalt at utgangen er 9 ved hjelp av den gitte ligningen f\venstre (2 \ høyre) = 9. Derfor må vi nå sette dem lik hverandre, og løse den lineære ligningen for den ukjente verdien av a.

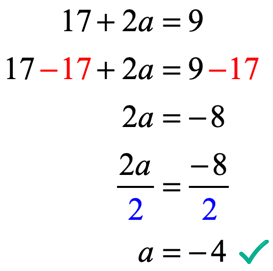
la oss verifisere om verdien av a = – \,4 i f(x) = 6{x^2} + ax – 7 kan gjøre den gitte tilstanden f\venstre( 2 \høyre) = 9 til en sann uttalelse.

det er sant! Derfor har vi løst for riktig verdi av a.