omzet is de hoeveelheid geld die een bedrijf binnenbrengt. In dit geval kan de omzet worden gevonden door de prijs per abonnement keer het aantal abonnees, of hoeveelheid te vermenigvuldigen. We kunnen variabelen invoeren, p voor prijs per abonnement en Q voor hoeveelheid, wat ons de vergelijking \text{Revenue}=pQ geeft.

omdat het aantal abonnees verandert met de prijs, moeten we een relatie vinden tussen de variabelen. We weten dat p=30 en Q=84.000. We weten ook dat als de prijs stijgt tot $ 32, De krant zou verliezen 5.000 abonnees, het geven van een tweede paar waarden, p=32 en Q=79.000. Hieruit kunnen we een lineaire vergelijking vinden met betrekking tot de twee grootheden. De helling wordt

\ begin{align}m& = \dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2} \\ &=-2.500 \end{align}

Dit vertelt ons dat het papier 2.500 abonnees zal verliezen voor elke dollar die ze de prijs verhogen. We kunnen dan oplossen voor de Y-as.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\text{Omzet}=pQ \\ &\text{Omzet}=p\left(-2,500 p+159,000\right) \\ &\text{Omzet}=-2,500{p}^{2}+159,000 p \end{align}

We hebben nu een kwadratische functie voor de opbrengst als functie van het abonnement. Om de prijs te vinden die de inkomsten voor de krant maximaliseert, kunnen we de vertex vinden.

\begin{align}h&=-\dfrac{159,000}{2\left(-2.500\right)} \\ &=31.8 \ end{align}

het model vertelt ons dat de maximale inkomsten zullen optreden als de krant $31,80 voor een abonnement in rekening brengt. Om te bepalen wat de maximale omzet is, evalueren we de omzetfunctie.

\begin{align}\text{maximum revenue}&=-2.500{\left(31.8\right)}^{2}+159.000\left(31.8\right) \\ &=\$2.528.100\hfill \end{align}

analyse van de oplossing

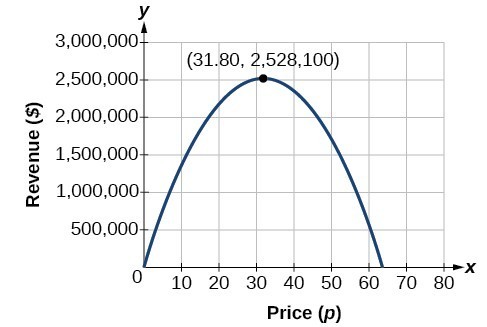
dit kan ook worden opgelost door de kwadratische grafiek. We kunnen de maximale omzet zien op een grafiek van de kwadratische functie.