przychód to ilość pieniędzy, jaką firma przynosi. W tym przypadku dochód można znaleźć, mnożąc cenę za subskrypcję razy liczbę abonentów lub ilość. Możemy wprowadzić zmienne, p dla ceny za subskrypcję i Q Dla ilości, dając nam równanie \ text{Revenue}=pQ.

ponieważ liczba abonentów zmienia się wraz z ceną, musimy znaleźć relację między zmiennymi. Wiemy, że obecnie p = 30 i Q=84 000. Wiemy również, że jeśli cena wzrośnie do 32 dolarów, Gazeta straci 5000 abonentów, dając drugą parę wartości, p = 32 I Q = 79 000. Z tego możemy znaleźć równanie liniowe odnoszące się do dwóch wielkości. Nachylenie będzie wynosić

\begin{align}m& = \ dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2} \ \ &=-2,500 \end{align}

to mówi nam, że gazeta straci 2,500 subskrybentów za każdego dolara, który podniesie cenę. Możemy wtedy rozwiązać punkt przecięcia osi y.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\text{Revenue}=PQ \\ &\text{Revenue}=p\left(-2,500 p+159,000\right) \\ &\text{revenue}=-2,500{P}^{2}+159,000 P \end{align}

mamy teraz funkcję kwadratową dla przychodów jako funkcję opłaty abonamentowej. Aby znaleźć cenę, która zmaksymalizuje przychody gazety, możemy znaleźć wierzchołek.

\begin{align}h&=-\dfrac{159,000}{2\left(-2,500\right)} \ \ &=31.8 \ end{align}

model mówi nam, że maksymalny dochód nastąpi, jeśli Gazeta pobierze 31,80 $za prenumeratę. Aby dowiedzieć się, jaki jest maksymalny przychód, oceniamy funkcję przychodów.

\begin{align}\text{maximum revenue}&=-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right) \\ &=\$2,528,100\hfill \end{align}

analiza rozwiązania

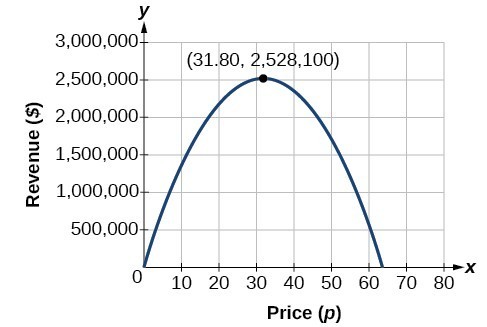
można to również rozwiązać poprzez wykresy kwadratowe. Możemy zobaczyć maksymalny przychód na wykresie funkcji kwadratowej.