mówiąc niezawodność, równoległe, oznacza dowolny z elementów w strukturze równoległej pozwalający na działanie systemu. Nie oznacza to, że są one fizycznie równoległe (we wszystkich przypadkach), ponieważ Kondensatory równolegle zapewniają określone zachowanie w obwodzie i jeśli jeden kondensator ulegnie awarii, układ może ulec awarii.
na tym prostym rysunku znajduje się n komponentów równolegle i każdy jeden komponent jest potrzebny do działania systemu.

Jeśli komponent #2 zawiedzie, Pozostałe pozwolą systemowi działać.

proste. I bardzo przydatne. Ta konstrukcja pozwala na ogólną poprawę niezawodności, nawet powyżej niezawodności poszczególnych komponentów. W przeciwieństwie do systemu seryjnego, w którym najsłabszy komponent ogranicza niezawodność, tutaj poprzez dodanie redundancji poprawia się niezawodność systemu.

rozważmy dwuskładnikowy układ równoległy. Jeśli oba komponenty działają, to system działa. Jeśli któryś z komponentów 1 lub 2 zawiedzie, system nadal działa. Wtedy i tylko wtedy, gdy oba komponenty ulegną awarii, system ulegnie awarii. W przeciwieństwie do systemu szeregowego, w którym jakakolwiek awaria powoduje awarię systemu, w tym prostym przykładzie muszą wystąpić dwa zdarzenia awarii, zanim system zawiedzie.

Jaka jest szansa na dwie porażki? Wzór opiera się na prawdopodobieństwie działania składnika 1 lub składnika 2. Bez wyprowadzania, możemy zapisać niezawodność 2-komponentowego systemu równoległego jako:

To get jest bardzo skomplikowane szybko z więcej niż trzema komponentami równolegle. Przed zbadaniem innego sposobu obliczania systemów równoległych należy najpierw wspomnieć o szczególnej sytuacji.

Gdy komponenty równolegle są takie same (niezawodność), powyższe upraszcza się do

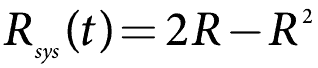
, co powinno być oczywiste.

często łatwiej jest wykonywać równoległe obliczenia systemu za pomocą nierzetelności lub 1 – R(t). Jest to również CDF lub F (t). Matematyka jest teraz bardziej jak system szeregowy z jedną poprawką. W ogólnym przypadku formuła niezawodności systemu dla systemu równoległego staje się

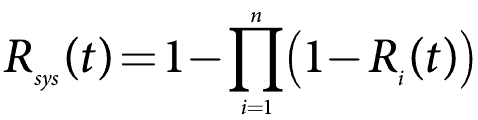
powiedzmy, że mamy pięć komponentów o niezawodności po jednym roku użytkowania, R(1), przy 90% lub 0.9. Oblicz niezawodność systemu.

korzystając z powyższego wzoru i ustawiając niezawodność każdego elementu na 0.9, znajdujemy

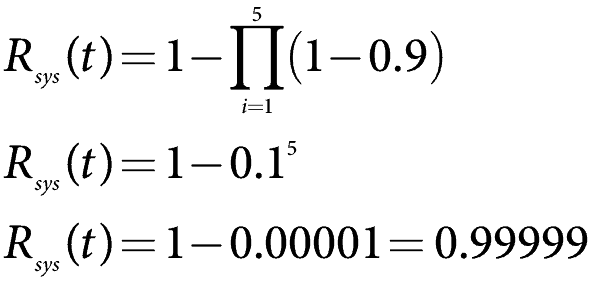
, który jest bardzo niezawodny.

dodawanie nadmiarowych Części do systemu jest kosztowne, ale w niektórych przypadkach jest to właściwe rozwiązanie, aby stworzyć system spełniający wymagania niezawodności. Oczywiście rzeczywiste systemy mają wiele odmian i komplikacji związanych z prostym ustawianiem komponentów równolegle. Systemy podziału obciążenia, gorący, ciepły lub zimny tryb czuwania, przełączanie lub głosowanie i wiele innych mogą skomplikować budowę równoległego systemu.

równoległe stosowanie komponentów jest jedynym sposobem na zwiększenie niezawodności systemu ponad granice niezawodności poszczególnych komponentów.

podobne:

schematy blokowe niezawodności przegląd i wartość (artykuł)

podział niezawodności (artykuł)

k Z N (artykuł)