o artigo abaixo mencionado fornece uma visão próxima sobre a função de produção de Cobb-Douglas.

A função de produção de Cobb-Douglas é baseada no estudo empírico da indústria manufatureira Americana feito por Paul H. Douglas e C. W. Cobb. É uma função linear homogênea de produção de grau Um que leva em conta dois insumos, trabalho e capital, para toda a produção do .industria.

a função de produção de Cobb-Douglas é expressa como:

Q = ALa Cß

Onde Q É produção e L E С São inputs de trabalho e capital, respectivamente. Um, um e β são positivos parâmetros onde a = a > S, β > S.

A equação diz que a saída depende, diretamente, L e C, e que parte da produção que não pode ser explicado por L e С é explicado por Uma que é a ‘residual’, muitas vezes chamado de mudança técnica.

A função de produção resolvido por Cobb-Douglas tinha 1/4 de contribuição de capital para o aumento da indústria transformadora e 3/4 de trabalho, de modo a que o C-D, a função de produção é

Q = AL3/4 C1/4

o que mostra a constante de retornos à escala, uma vez que o total dos valores de L e С é igual a: (3/4 + 1/4), isto é,(a + β = 1) . O coeficiente de mão-de-obra na função C-D mede o aumento percentual em (Q que resultaria de um aumento de 1% em L, mantendo O С como constante.

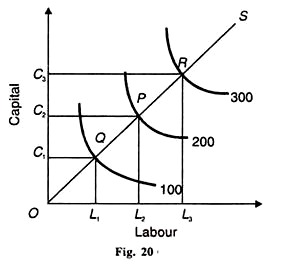
da mesma forma, В é o aumento percentual em Q que resultaria de um aumento de 1% em C, mantendo L como constante. A função de produção de C-D que mostra retornos constantes à escala é representada na Figura 20. A entrada de mão-de-obra é tomada no eixo horizontal e o capital no eixo vertical. para produzir 100 unidades de produção, utilizam-se Unidades de capital e unidades de trabalho. Se a produção fosse dobrada para 200, os insumos de trabalho e de capital teriam que ser dobrados. ОС é exatamente o dobro de ОС1 e de OL2 é o dobro de OL2.

similarmente, se a produção for aumentada três vezes para 300, as unidades de trabalho e capital terão de ser aumentadas três vezes. OC3 e OL3 são três vezes maiores que ОС1, e OL1, respectivamente. Outro método é tomar a linha de escala ou caminho de expansão conectando os pontos de equilíbrio Q, P E R. OS é a linha de escala ou caminho de expansão unindo esses pontos. mostra que os isoquantes 100, 200 e 300 são equidistantes. Assim, na linha de escala oq = QP = PR, que mostra que quando o capital e o trabalho são aumentados em proporções iguais, a produção também aumenta na mesma proporção.

críticas à função de produção C-D:

A função de produção C-D foi criticada por Arrow, Chenery, Minhas e Solow como discutido abaixo:

1. A função de produção C-D considera apenas dois insumos, trabalho e capital, e negligencia alguns insumos importantes, como as matérias-primas, que são utilizadas na produção. Portanto, não é possível generalizar esta função a mais de duas entradas. 2. Na função de produção C-D, surge o problema da mensuração do capital, pois só toma a quantidade de capital disponível para a produção. Mas a plena utilização do capital disponível só pode ser feita em períodos de pleno emprego. Isto é irrealista porque nenhuma economia está sempre totalmente empregada.

3. A função de produção C-D é criticada porque mostra retornos constantes à escala. Mas retornos constantes à escala não são uma realidade, pois tanto retornos crescentes ou decrescentes à escala são aplicáveis à produção.

não é possível alterar todos os inputs para trazer uma mudança proporcional nos outputs de todas as indústrias. Algumas entradas são escassas e não podem ser aumentadas na mesma proporção que Entradas abundantes. Por outro lado, insumos como máquinas, empreendedorismo, etc. são indivisíveis. À medida que a produção aumenta devido à utilização de factores indivisíveis para a sua capacidade máxima, o custo unitário diminui.

assim, quando o fornecimento de insumos é escasso e as indivisibilidades estão presentes, retornos constantes à escala não são possíveis. Sempre que as unidades de diferentes insumos são aumentadas no processo de produção, as economias de escala e a especialização levam ao aumento dos retornos à escala. na prática, porém, nenhum empresário gostaria de aumentar as várias unidades de inputs a fim de ter um aumento proporcional da produção. Seu esforço é ter um aumento mais do que proporcional na produção, embora a diminuição dos retornos à escala também não são descartados. 4. A função de produção C-D baseia-se no pressuposto da substituibilidade dos factores e negligencia a complementaridade dos factores. 5. Esta função baseia-se no pressuposto de uma concorrência perfeita no mercado dos factores, o que é irrealista. Se, no entanto, esta hipótese for suprimida, os coeficientes α e β não representam as partes dos factores.

6. Uma das fraquezas da função C-D é o problema da agregação. Este problema surge quando esta função é aplicada a todas as empresas de uma indústria e a toda a indústria. Nesta situação, haverá muitas funções de produção de baixa ou alta agregação. Assim, a função C-D não mede o que pretende medir.

conclusão:

assim, a praticabilidade da função de produção de C-D na indústria transformadora é uma proposta duvidosa. Isto não é aplicável à agricultura em que, para cultivo intensivo, o aumento das quantidades de insumos não aumentará proporcionalmente a produção. Mesmo assim, não se pode negar que o retorno constante à escala é uma etapa na vida de uma empresa, indústria ou economia. É outra coisa que esta etapa pode vir depois de algum tempo e por um curto período de tempo.

é importante:

apesar destas críticas, a função C-D é de grande importância. 1. Tem sido amplamente utilizado em estudos empíricos das indústrias transformadoras e em comparações interindústrias. 2. É utilizado para determinar as partes relativas do trabalho e do capital na produção total. 3. É usado para provar o teorema de Euler. 4. Os seus parâmetros a e b representam coeficientes de elasticidade que são utilizados para comparações intersectoriais. 5. Esta função de produção é linear homogênea de grau Um que mostra retornos constantes à escala, Se α + β = 1, há retornos crescentes à escala e Se α + β < 1, há retornos decrescentes à escala.

6. Os economistas estenderam esta função de produção a mais de duas variáveis.