Notação de Função e de Como Avaliar uma Função
O comum notação de uma função é normalmente escrito como
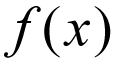
não acho isso muito literalmente, isto é, f é ser multiplicado para x. Em vez disso, considere isso como uma expressão matemática que é lido como

OU

Funções também pode ser escrito de formas diferentes a utilização de outras variáveis, tais como:
- g(x), h(x) e k(x)
além disso, funções pode levar outros valores de entrada diferente de x.
- f(a), h(r), e k(m)
A idéia-chave é sempre lembrar-se de que a variável de fora do parêntese é o “nome” da função, enquanto que a variável entre parênteses é o valor de entrada da função.
Por exemplo, o seguinte é chamada de função de k, com um valor de entrada de m.
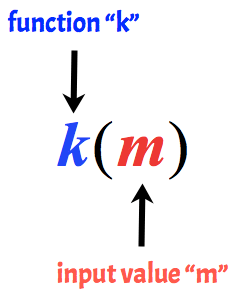
Exemplos Básicos de Avaliação de Funções
Exemplo 1: Avaliar a função .
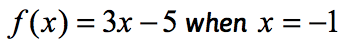
Esta é a notação normal da função onde a função é f enquanto o valor de entrada é x. Para avaliar uma função, o que nós queremos é substituir cada ocorrência de x na expressão e, em seguida, simplificar.
desde x = – 1, nós substituímos este valor na função e simplificamos. Ao fazê-lo, temos uma solução que se parece com esta.
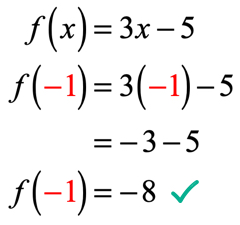
Exemplo 2: avaliar a função .
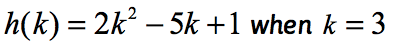
Observe que a função aqui é h e o valor de entrada é k. Assim como em nosso exemplo anterior, nós queremos substituir qualquer que seja o valor numérico atribuído a k na função dada, e simplificar.
Desde k = 3, a sua solução deve ser semelhante a este
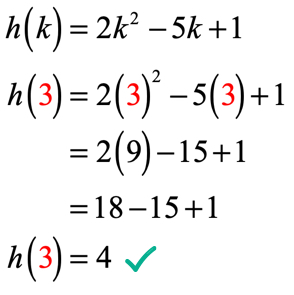
Exemplo 3: Avaliar cada valor de x na tabela abaixo, usando a função abaixo. Traçar os pontos no eixo xy e ligar os pontos para revelar o gráfico da função.
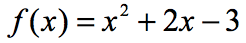

Desde há sete x-entradas, o que significa que iremos avaliar a função sete vezes também. Tente resolver isto sozinho e depois volte para verificar as suas respostas.se o fez correctamente, estes são os valores:
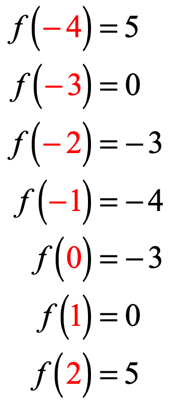
podemos agora colocar esses valores de saída na tabela.
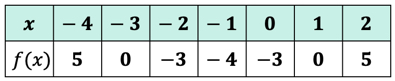
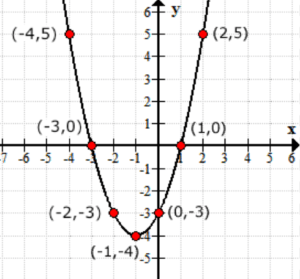
Pensar que os valores de saída da função f\left( x \right) como os valores de y. É assim que o gráfico se parece no eixo xy.
Intermediário Exemplos de Avaliação de Funções
Exemplo 4: Dado que g\left( x \right) = {x^2} – 3x + 1, encontrar g\left( {2x – 1} \right).
em exemplos anteriores, temos vindo a avaliar uma função por um número. Desta vez, o valor de entrada não é mais um valor numérico fixo, mas sim uma expressão. Pode parecer complicado, mas o procedimento continua o mesmo.
iremos substituir cada instância de x em g\esquerda (x \direita) pelo valor de entrada que é 2x – 1. Simplifique esquartejando o binômio, aplicando a propriedade distributiva e combinando termos similares.
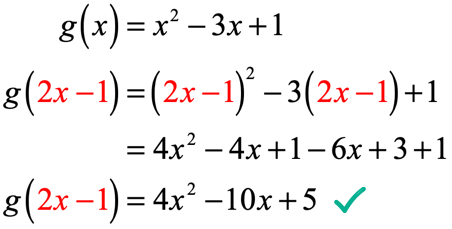
Exemplo 5: Dado que p\left( x \right) = {{4x – 1} \over x} , avaliar p\left( 1 \right) – p\left( { – 1} \right).
o problema pode parecer intimidante no início, mas uma vez que analisá-lo e aplicar o que já sabemos sobre como avaliar funções, isso não deve ser tão ruim!
o Que precisamos fazer aqui é avaliar a função em x = 1, então, subtrair o valor da função quando avaliada em x = – \,1.
tenha muito cuidado ao substituir os valores e durante o processo de simplificação. Se você não tiver cuidado em cada passo, é muito fácil cometer erros quando você adicionar, subtrair, multiplicar ou dividir números positivos e negativos.
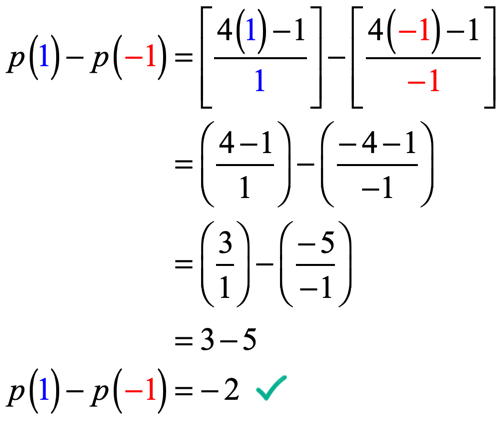
Avançado Exemplo de Aplicação do Conceito de Avaliação de Funções
Exemplo 6: Se f\left( 2 \right) = 9, encontre o valor de a na função abaixo.
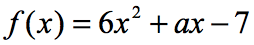
Na equação, f\left( 2 \right) = 9, somos informados de que, se a entrada da função é 2; a saída da função será 9. Uma vez que a função é dada a nós, nosso primeiro passo é pelo menos substituir o valor de 2 e, em seguida, simplificar. Isto é o que vamos conseguir.
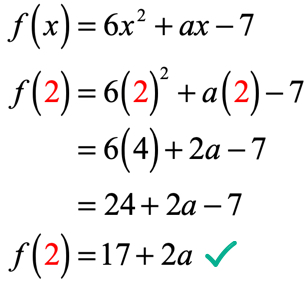
A saída da função depois de avaliar em x = 2 é 17 + 2a. Lembre-se, somos também informados de que a saída é 9, usando a equação dada f\left( 2 \right) = 9. Portanto, o que precisamos fazer agora é definir-los iguais uns aos outros, e resolver a equação linear para o valor desconhecido de um.
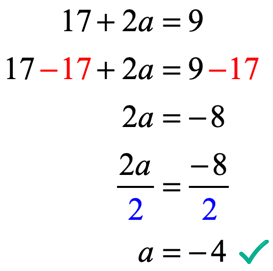
Vamos verificar se o valor de a = – \,4 f(x) = 6{x^2} + ax – 7 pode melhorar a condição dada f\left( 2 \right) = 9 para ser uma declaração verdadeira.

É verdade! Assim, resolvemos com sucesso o valor correto de A.
Leave a Reply