um tensor é um conjunto de dados (números, funções, etc.) que é expandida em qualquer número (0 e maior) de dimensões. O número de dimensões é chamado rank de tensor.

Rank 0 tensor

um tensor que não tem dimensões (0).

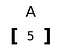
Rank 1 tensor

Um tensor que é expandida em apenas uma dimensão.

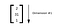
Rank 2 tensor

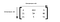
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

Escalar

Um escalar é de 0 rank tensor. Em física, várias quantidades são representadas como um escalar, como : distância (500 km), temperatura (10ºC), velocidade (34 km/h), etc.

Vector

um tensor rank 1 é chamado de vector. Quantidades físicas tais como Velocidade (10 m/s), deslocamento (54 m para leste), campo eletromagnético (1 V/m).

diferença entre escalar e vector :

uma quantidade que não requer informações adicionais (como direção) com ela (como, temperatura) é representada como escalar. Considerando que, uma quantidade que precisa de direção a ser especificada ao lado de sua magnitude é representada com um vetor (como, campo elétrico).

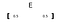
Um vector é indicado com a letra negrito (como “E” ) ou uma seta acima a letra.

para traçar um vetor, usamos seus elementos como o valor das coordenadas (eixo x, y E z, respectivamente). Aqui, o primeiro elemento (0.5) é tomado como x valor e o segundo elemento (também 0.5) é tomado como y valor (se tivéssemos três elementos, o terceiro teria sido z valor).

Depois de traçar o vetor como um ponto colocamos uma seta para ele, desde a origem(0,0).

Um vetor é simplesmente uma matriz que tem uma linha (chamada vetor coluna) ou uma coluna (chamada vetor linha).

Matrix

a matrix é um tensor rank 2. Já vimos o matrix antes.

um tensor com classificação superior a 2 é simplesmente chamado “tensor” (não existe um nome específico para tensores com classificação superior a 2).

conceito de tensor generaliza as matrizes, vetores e escalares sob um mesmo teto (todos eles são tensores, mas com diferentes níveis).matrizes como produto de vetores :

quando dois vetores são multiplicados eles formam uma matriz.

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Assim, algumas matrizes poderiam ser divididas como um produto de dois vetores.