An alternative normality test is the Shapiro-Wilk test.o que é um teste de normalidade de Kolmogorov-Smirnov?

What is a Kolmogorov-Smirnov normality test?

o teste de Kolmogorov-Smirnov examina se é provável que as pontuações
sigam alguma distribuição em alguma população.Para evitar confusão, há 2 testes Kolmogorov-Smirnov:

• há uma amostra de teste Kolmogorov-Smirnov para testar se uma variável segue uma dada distribuição em uma população. Esta ” distribuição dada “é geralmente-nem sempre – a distribuição normal, daí o”teste de normalidade de Kolmogorov-Smirnov”.
• Há também as amostras independentes (muito menos comuns) Kolmogorov-Smirnov teste para testar se uma variável tem distribuições idênticas em 2 populações.

em Teoria, “Teste de Kolmogorov-Smirnov” pode referir-se a qualquer teste (mas geralmente refere-se ao teste de Kolmogorov-Smirnov de uma amostra) e deve ser evitado. A propósito, ambos os testes de Kolmogorov-Smirnov estão presentes no SPSS.

teste de Kolmogorov-Smirnov-exemplo simples

assim, eu tenho uma população de 1.000.000 de pessoas. Penso que os seus tempos de reacção a uma determinada tarefa estão perfeitamente distribuídos. Provo 233 destas pessoas e medo os seus tempos de reacção.
agora a distribuição de frequência observada destes provavelmente diferirá um pouco-mas não muito – de uma distribuição normal. Então eu faço um histograma sobre os tempos de reação observados e sobreponho uma distribuição normal com a mesma média e desvio padrão. O resultado é mostrado abaixo.

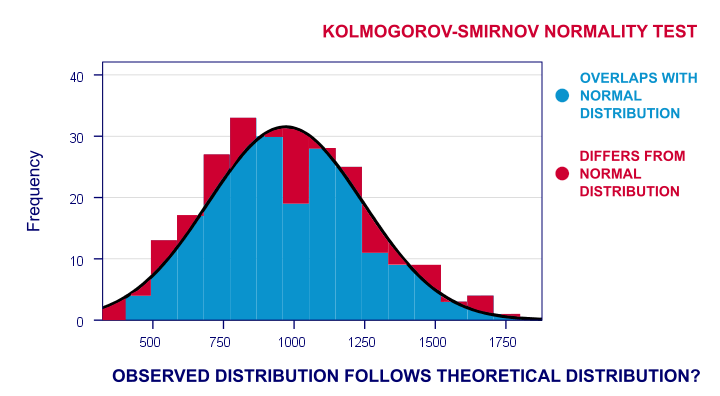
a distribuição de frequência das minhas pontuações não se sobrepõe inteiramente à minha curva normal. Agora, eu poderia calcular a porcentagem de casos que se desviam da curva normal-a porcentagem de áreas vermelhas no gráfico. Esta porcentagem é uma estatística de teste: ela expressa em um único número o quanto meus dados diferem da minha hipótese nula. Assim, indica em que medida as pontuações observadas se desviam de uma distribuição normal.agora, se minha hipótese nula é verdadeira, então essa percentagem de desvio provavelmente deve ser bastante pequena. Isto é, um pequeno desvio tem um alto valor de probabilidade ou valor p.inversamente, uma grande percentagem de desvio é muito improvável e sugere que os meus tempos de reacção não seguem uma distribuição normal em toda a população. Então um grande desvio tem um baixo valor p. Como regra geral, wereject a hipótese nula se p < 0.05.Então, se p < 0.05, não acreditamos que a nossa variável segue uma distribuição normal na população.

Kolmogorov-Smirnov Test Statistic

então essa é a maneira mais fácil de entender como funciona o teste de normalidade de Kolmogorov-Smirnov. Computacionalmente, no entanto, funciona de forma diferente: compara as frequências relativas observadas versus as esperadas, como mostrado abaixo.

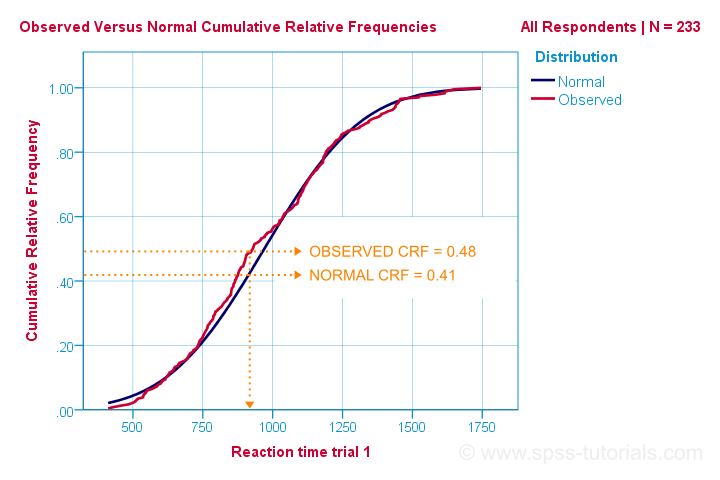
O teste de Kolmogorov-Smirnov usa o máximo valor absoluto da diferença entre essas curvas como seu teste estatístico indicado por D. neste gráfico, a máxima diferença absoluta D é (0.48 – 0.41 =) 0.07 e ocorre em um tempo de reação de 960 milissegundos. Tenha em mente que D = 0,07 como vamos encontrá-lo em nossa saída SPSS em um minuto.

o teste de Kolmogorov-Smirnov em SPSS

Existem 2 maneiras de executar o teste em SPSS:

• NPAR TESTS como encontrado em Analisar Testes não-paramétricos Legado caixas de diálogo 1-Exemplo de K-S… é o nosso método de escolha porque cria uma saída bem detalhada.
• examinar variáveis de análise estatísticas descritivas Explorar é uma alternativa. Este comando executa tanto o teste Kolmogorov-Smirnov como o teste de normalidade Shapiro-Wilk.
  Note that EXAMINE VARIABLES uses listwise exclusion of missing values by default. Então se eu testar 5 variáveis, meus 5 testes só usam casos que não têm falhas em nenhuma dessas 5 variáveis. Normalmente não é isto que queres, mas vamos mostrar como evitar isto.

demonstraremos ambos os métodos usando speedtasks.sav em todo o corpo, parte da qual é mostrada abaixo.

a Nossa principal questão de investigação iswhich do tempo de reação variáveis é provável
ser normalmente distribuído em nossa população?Estes dados são um exemplo de livro de porque você deve inspecionar cuidadosamente seus dados antes de começar a editá-los ou analisá-los. Vamos fazer isso e executar alguns histogramas a partir da sintaxe abaixo.

Result

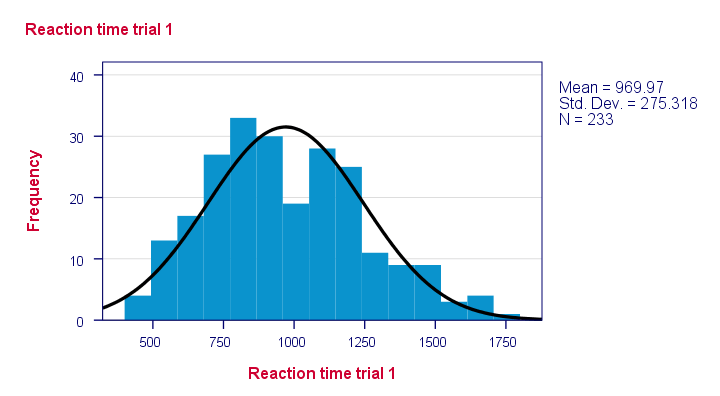
Note que algumas distribuições não parecem plausíveis de todo. Mas quais serão normalmente distribuídas?

SPSS o teste de Kolmogorov-Smirnov de NPAR TESTS

a Nossa opção preferencial para a execução do teste de Kolmogorov-Smirnov é underAnalyze Testes não-paramétricos Legado caixas de diálogo 1-Exemplo de K-S… como mostrado abaixo.

em seguida, basta preencher a janela como mostrado abaixo.

ao carregar em Colar, obtém-se a sintaxe abaixo. Vamos a isso.

Kolmogorov-Smirnov Test Syntax from Nonparametric Tests

Resultados

Primeiro, note que a estatística de teste a nossa primeira variável é 0.073 -tal como vimos em nossos cumulativa freqüência relativa gráfico um pouco mais cedo no. O gráfico contém exactamente os mesmos dados em que fizemos o teste para que estes resultados convergam.em relação à nossa pergunta de pesquisa: apenas os tempos de reação para o ensaio 4 parecem ser normalmente distribuídos.

SPSS Kolmogorov-Smirnov test from EXAMINE VARIABLES

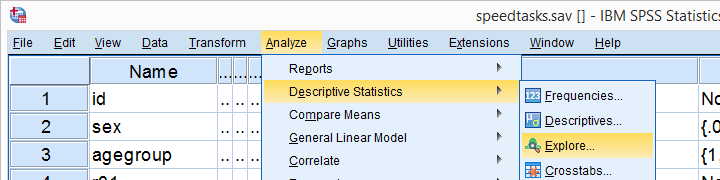
An alternative way to run the Kolmogorov-Smirnov test starts from Analyze Descriptive Statistics Exploreas shown below.

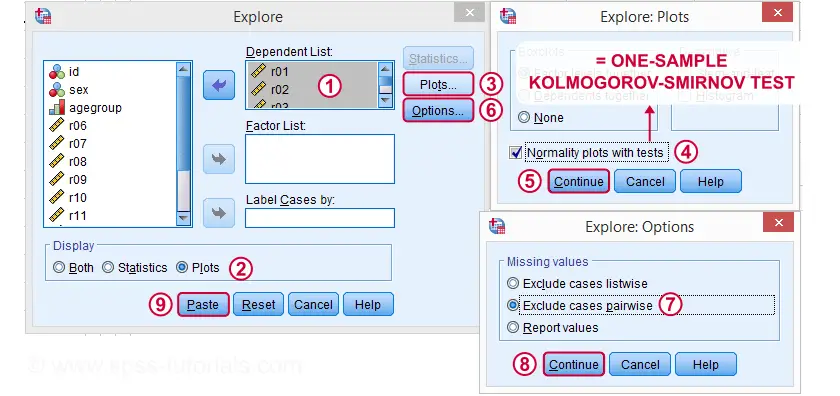
Teste de Kolmogorov-Smirnov Sintaxe de Testes não-paramétricos

Results

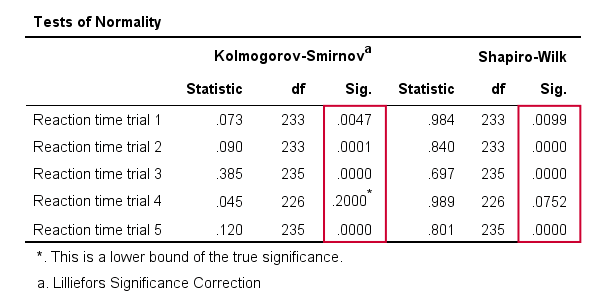
As a rule of thumb, we conclude thata variable is not normally distributed if “Sig.” < 0.05.Assim, tanto o teste de Kolmogorov-Smirnov como os resultados do teste de Shapiro-Wilk sugerem que apenas o ensaio 4 do tempo de reacção segue uma distribuição normal em toda a população.além disso, note que os resultados do teste de Kolmogorov-Smirnov são idênticos aos obtidos dos testes NPAR.

Relatório de um Teste de Kolmogorov-Smirnov

Para o relatório de resultados de nossos testes APA diretrizes, nós vamos escrever algo como”um teste de Kolmogorov-Smirnov indica que os tempos de reação no teste 1 não seguem uma distribuição normal, D(233) = 0.07, p = 0,005.”Para variáveis adicionais, tentar encurtar isso, mas certifique-se de que você incluir

• D (para “diferença”), o teste de Kolmogorov-Smirnov estatística,
• df, os graus de liberdade (que é igual a N) e
• p, significância estatística.

Wrong Results in SPSS?

Se você é um estudante que só quer passar um teste, você pode parar de ler agora. Siga os passos que discutimos até agora e ficará bem.

Right, now let’s run the exact same tests again in SPSS version 18 and take a look at the output.

In this output, the exact p-values are included and-felizmente – they are very close to the asymptotic p-values. Menos felizmente, porém, os resultados da versão 18 do SPSS são muito diferentes da versão 24 do SPSS, relatada até agora.
The reason seems to be the Lilliefors significance correction which is applied in newer SPSS versions. O resultado parece ser que os níveis de significância assintótica diferem muito mais do significado exato do que quando a correção não está implícita. Isso levanta sérias dúvidas sobre a correção dos “resultados Lilliefors” -o padrão em versões mais recentes SPSS.evidências convergentes para esta sugestão foram recolhidas pelo meu colega Alwin Stegeman que reencaminhou todos os testes em Matlab. Os resultados do Matlab concordam com os resultados do SPSS 18 e-portanto – não com os resultados mais recentes.

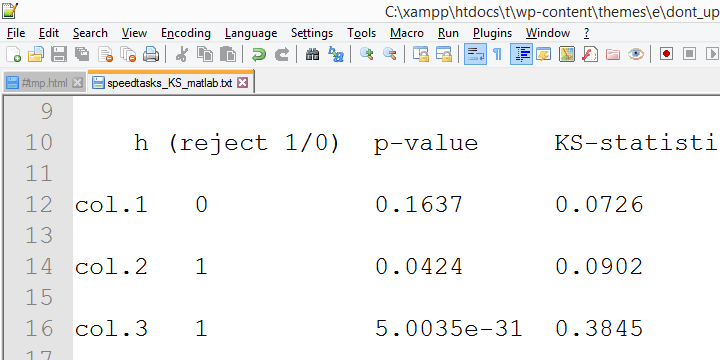
teste de Kolmogorov-Smirnov o teste de normalidade – Utilidade Limitada

O teste de Kolmogorov-Smirnov é, muitas vezes, para testar a suposição de normalidade exigida por muitos testes estatísticos, tais como ANOVA, o teste-t e muitos outros. No entanto, é quase rotineiramente ignorado que tais testes são robustos contra uma violação desta suposição se o tamanho da amostra é razoável, digamos N ≥ 25.A razão subjacente para isso é o teorema do limite central. Por conseguinte, os testes de normalidade só são necessários para pequenas dimensões da amostra se o objectivo for satisfazer o pressuposto de normalidade.infelizmente, pequenos tamanhos de amostra resultam em baixa potência estatística para testes de normalidade. Isto significa que desvios substanciais em relação à normalidade não resultarão em significância estatística. O teste diz que não há desvio da normalidade enquanto é enorme. Em suma, a situação em que são necessários testes de normalidade-pequenos tamanhos de amostra – é também a situação em que eles têm um desempenho deficiente.obrigado pela leitura.