intäkter är hur mycket pengar ett företag tar in. I det här fallet kan intäkterna hittas genom att multiplicera priset per prenumeration gånger antalet abonnenter eller kvantitet. Vi kan introducera variabler, p för pris per prenumeration och Q för kvantitet, vilket ger oss ekvationen \text{intäkter}=pQ.

eftersom antalet abonnenter ändras med priset måste vi hitta en relation mellan variablerna. Vi vet att för närvarande p = 30 och Q=84 000. Vi vet också att om priset stiger till $32 skulle tidningen förlora 5 000 abonnenter, vilket ger ett andra par värden, p=32 och Q=79 000. Från detta kan vi hitta en linjär ekvation som relaterar de två kvantiteterna. Lutningen kommer att vara

\ begin{align}m&= \ dfrac{79,000 – 84,000}{32 – 30} \\ &=\dfrac{-5,000}{2} \\ &=-2,500 \end{align}

detta berättar papperet kommer att förlora 2,500 abonnenter för varje dollar de höjer priset. Vi kan sedan lösa för y-avlyssningen.

\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}

This gives us the linear equation Q=-2,500p+159,000 relating cost and subscribers. We now return to our revenue equation.

\begin{align}&\text{Revenue}=pQ \\ &\text{Revenue}=p\vänster(-2 500 p+159 000\höger) \\ &\text{intäkter}=-2 500{p}^{2}+159 000 p \end{align}

Vi har nu en kvadratisk funktion för intäkter som en funktion av prenumerationsavgiften. För att hitta det pris som maximerar intäkterna för tidningen kan vi hitta vertexen.

\ börja{justera}h &=-\dfrac{159,000}{2\vänster(-2,500\höger)} \\ & =31.8 \ end{align}

modellen berättar att den maximala intäkterna kommer att inträffa om tidningen tar ut $31,80 för en prenumeration. För att hitta vad den maximala intäkterna är utvärderar vi intäktsfunktionen.

\begin{align}\text{maximala intäkter}&=-2 500{\vänster(31,8\höger)}^{2}+159 000\vänster(31,8\höger) \\ &=\$2,528,100\hfill \end{align}

analys av lösningen

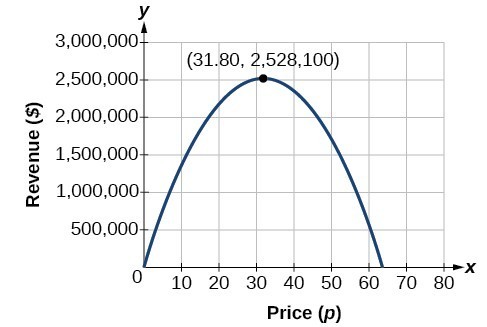
detta kan också lösas genom att grafera kvadratiska. Vi kan se de maximala intäkterna på en graf över den kvadratiska funktionen.