College Physics
shrnutí
- popište účinky magnetické síly na vodič nesoucí proud.
- Vypočítejte magnetickou sílu na vodiči nesoucím proud.
Protože poplatky obvykle nemůže uniknout vodiče, magnetická síla na poplatky pohybující se ve vodiči se přenáší na vodič sám.
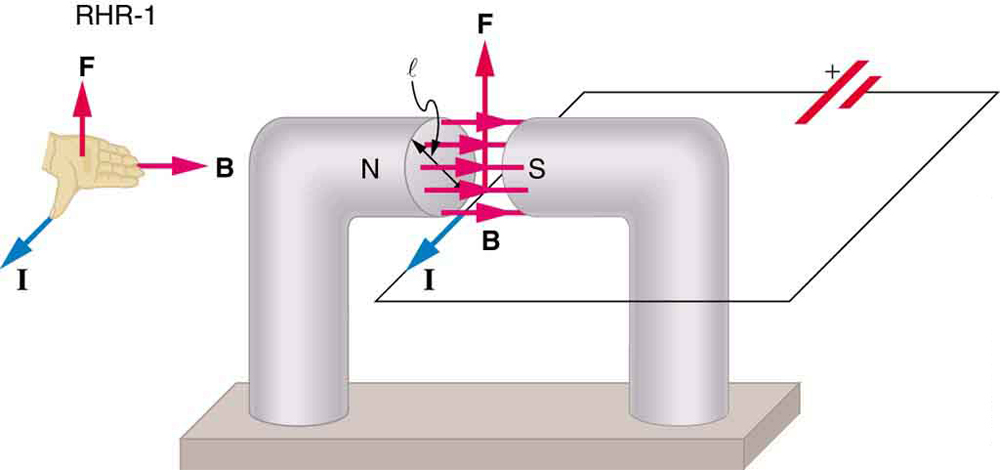
můžeme odvodit výraz pro magnetické síly na proudu tím, že součet magnetických sil na jednotlivých poplatků. (Síly přidat, protože jsou ve stejném směru.) Síla na jednotlivý náboj pohybující se rychlostí driftu vdvd je dána \boldsymbol{F = qv_dB \; \ textbf{sin} \; \theta}. Přičemž \boldsymbol{B} musí být rovnoměrné po délce drátu \boldsymbol{l} a nula jinde, celková magnetická síla na vodič je pak \boldsymbol{F = (qv_dB \;\textbf{sin} \;\theta)(N)}, kde \boldsymbol{N} je počet nosičů náboje je v části vodiče o délce \boldsymbol{l}. Teď, \boldsymbol{N=nV}, kde \boldsymbol{n} je počet nosičů náboje na jednotku objemu a \boldsymbol{V} je objem drátu v poli. Upozorňuje, že \boldsymbol{V=Al}, kde \boldsymbol{A} je plocha průřezu vodiče, pak síla působící na drát je \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta)(nAl)}.
Protože \boldsymbol{nqAv_d = I} (viz Kapitola 20.1 Aktuální),
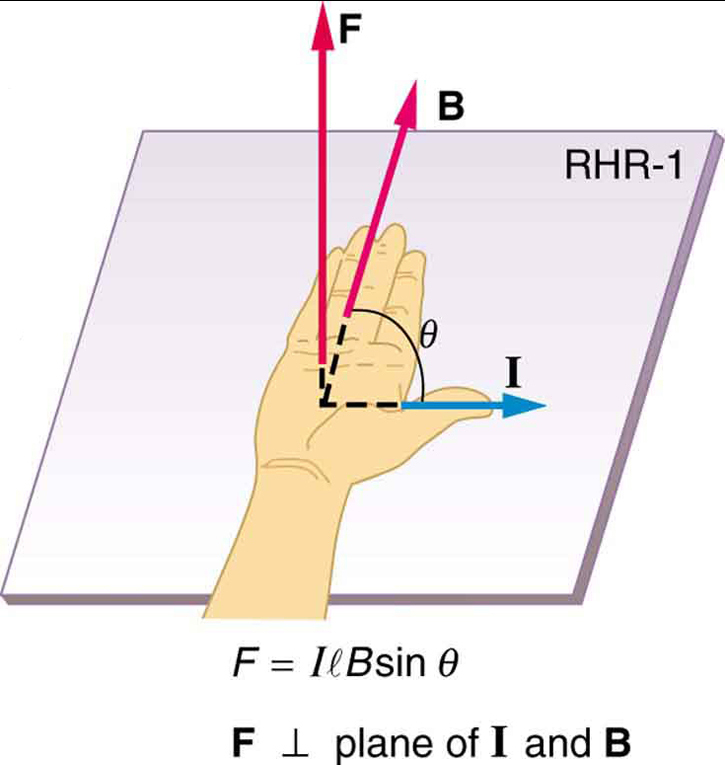
je rovnice pro magnetické síly na délku \boldsymbol{l} z drátu nést proud \boldsymbol{I} v homogenním magnetickém poli \boldsymbol{B}, jak je znázorněno na Obrázku 2. Když vydělíme obě strany tohoto výrazu \boldsymbol{l}, zjistíme, že magnetické síly na jednotku délky vodiče v jednotné pole je \boldsymbol{\frac{F}{l} = IB \;\textbf{sin} \;\theta}. Směr této síly je dán RHR-1, palcem ve směru proudu \ boldsymbol{I}. Pak, s prsty ve směru \boldsymbol{B}, kolmo k dlani bodů ve směru \boldsymbol{F}, jako na Obrázku 2.
Výpočet Magnetické Síly na Proudu-nosné Dráty: Silné Magnetické Pole
Výpočet síly působící na vodiče je znázorněno na Obrázku 1, vzhledem k tomu, \boldsymbol{B = 1.50 \;\textbf{T}}, \boldsymbol{l = 5.00 \;\textbf{cm}}, \boldsymbol{I = 20.0 \;\textbf{A}}.
Strategie
platnost lze nalézt u uvedených informací pomocí \boldsymbol{F = IlB \;\textbf{sin} \;\theta} a upozorňuje, že úhel \boldsymbol{\theta} mezi \boldsymbol{I} a \boldsymbol{B} \boldsymbol{90 ^{\circ}}, tak, že \boldsymbol{\textbf{sin} \;\theta = 1}.
řešení
zadání zadaných hodnot do \boldsymbol{F = IlB \;\textbf{sin} \theta} výnosy
jednotky pro tesla jsou \boldsymbol{1 \;\textbf{T} = \frac{\textbf{N}}{\textbf{A} \cdot \; \textbf{m}}}; to znamená,
diskuse
toto velké magnetické pole vytváří významnou sílu na malou délku drátu.
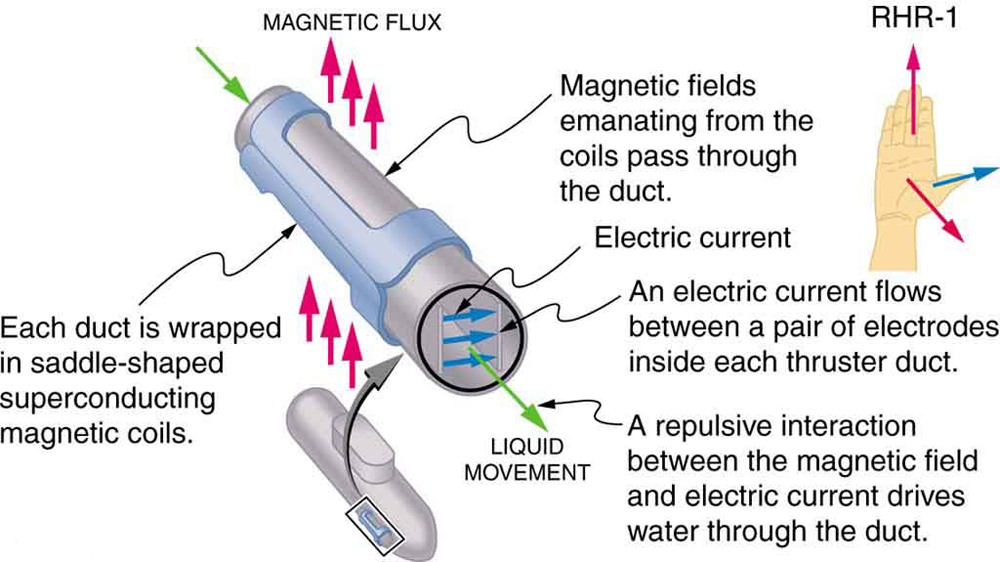
magnetická síla na vodičích nesoucích proud se používá k přeměně elektrické energie na práci. (Motory jsou ukázkovým příkladem-používají smyčky drátu a jsou zvažovány v další části.) Magnetohydrodynamika (MHD) je technický název daný chytré aplikaci, kde magnetická síla pumpuje tekutiny bez pohyblivých mechanických částí. (Viz Obrázek 3.)
silné magnetické pole se aplikuje přes trubice a proud prochází tekutina v pravém úhlu k oblasti, což v platnost kapaliny paralelní osy trubky, jak je znázorněno. Absence pohyblivých částí činí tento atraktivní pro pohyb horké, chemicky aktivní látky, jako je kapalný sodík používaný v některých jaderných reaktorech. Experimentální umělá srdce testují touto technikou čerpání krve, možná obcházejí nepříznivé účinky mechanických čerpadel. (Buněčné membrány, jsou však ovlivněny velkými poli třeba v MHD, zpoždění jeho praktickou aplikaci u člověka.) Byl navržen MHD pohon pro jaderné ponorky, protože by mohl být podstatně tišší než běžné vrtulové pohony. Odstrašující hodnota jaderných ponorek je založena na jejich schopnosti skrýt a přežít první nebo druhý jaderný úder. Jak pomalu rozebíráme naše arzenály jaderných zbraní, ponorková větev bude poslední, která bude vyřazena z provozu kvůli této schopnosti (viz obrázek 4.) Stávající jednotky MHD jsou těžké a neefektivní—je zapotřebí mnoho vývojových prací.
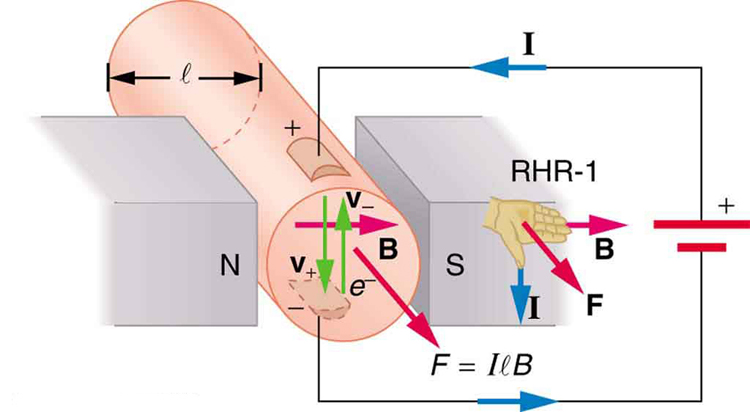
- magnetická síla na proud vodiče je dána tím, že
\boldsymbol{F = IlB \;\textbf{sin} \;\theta},
, kde \boldsymbol{I} je aktuální, \boldsymbol{l} je délka přímého vodiče v homogenním magnetickém poli \boldsymbol{B}, a \boldsymbol{\theta} je úhel mezi \boldsymbol{I} a \boldsymbol{B}. Síla následuje RHR-1 palcem ve směru \boldsymbol{I}.
koncepční otázky
1: Nakreslete náčrt situace na obrázku 1 ukazující směr elektronů nesoucích proud a pomocí RHR-1 Ověřte směr síly na drátu.
2: Ověřte, že směr síly v MHD disk, jako je to na Obrázku 3, nezávisí na znamení poplatky proud přes kapaliny.
3: Proč by magnetohydrodynamický pohon fungoval lépe v oceánské vodě než ve sladké vodě? Taky, proč by supravodivé magnety byly žádoucí?
4: Což s větší pravděpodobností ruší čtení kompasu, střídavý proud v lednici nebo stejnosměrný proud při nastartování auta? Vysvětlit.
Problémy & Cvičení
1: Jaký je směr magnetické síly na proudu v každé ze šesti případech na Obrázku 5?
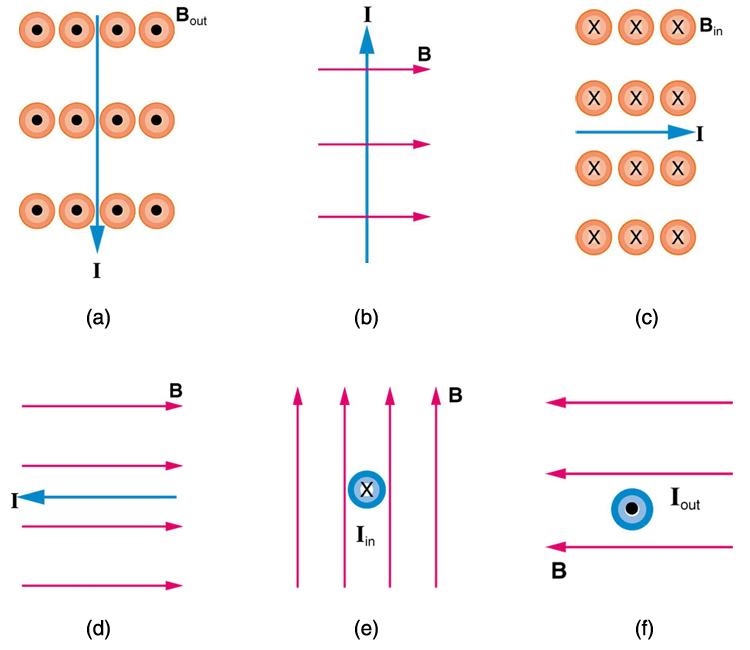
2: Jaký je směr proudu, který prožívá magnetické síly zobrazené v každém ze tří případů v Obrázku 6, za předpokladu, že stávající kolmá k \boldsymbol{B}?
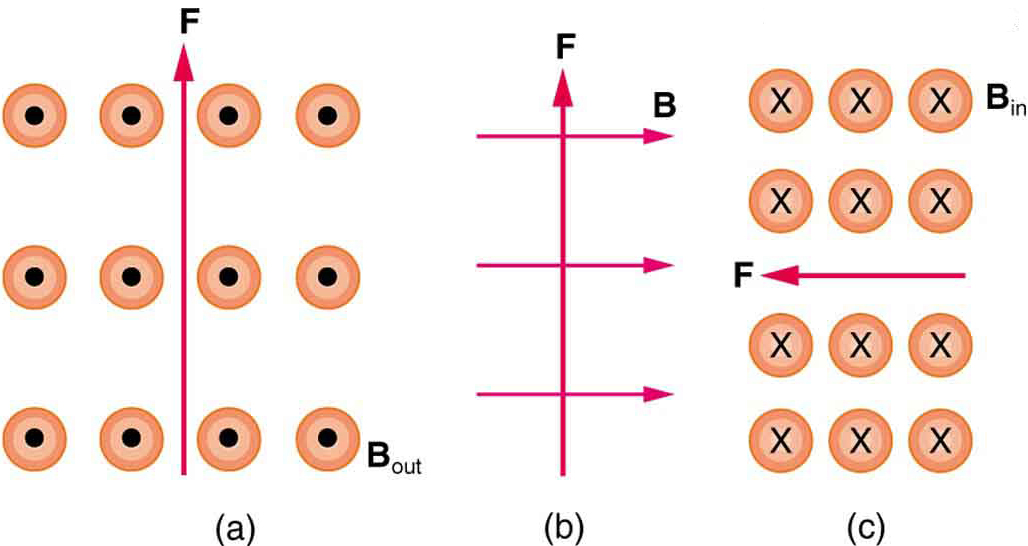
3: Jaký je směr magnetického pole, které vytváří magnetické síly je znázorněno na proudy v každém ze tří případů na Obrázku 7, za předpokladu, že \boldsymbol{B} je kolmý k \boldsymbol{I}?
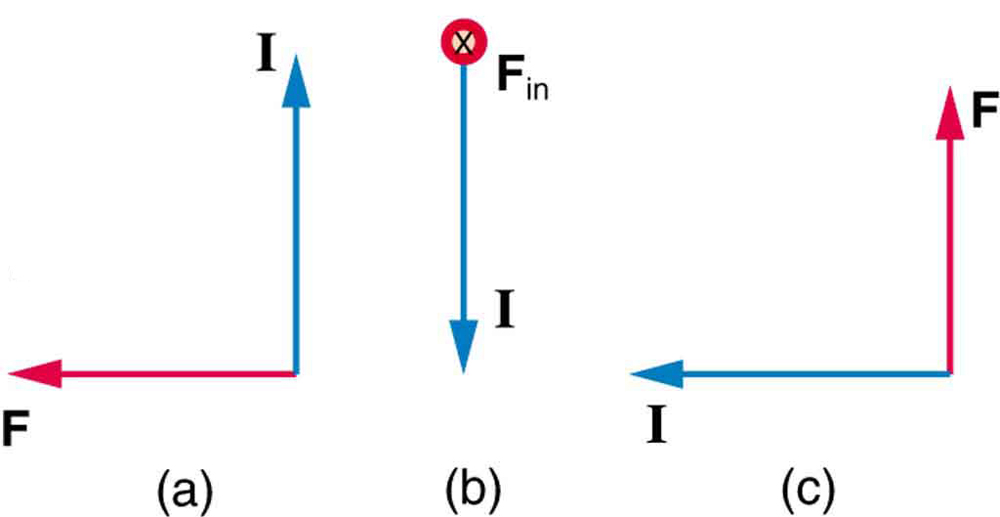
4: (a) Co je to síla na metr na blesk na rovníku, která nese 20 000 kolmo k Zemi \boldsymbol{3.00 \times 10^{-5} – \textbf{T}} pole? (b) jaký je směr síly, pokud je proud přímo nahoru a směr zemského pole je způsoben severně, rovnoběžně se zemí?
5: (a) stejnosměrné vedení pro systém lehké kolejnice nese 1000 A pod úhlem \ boldsymbol{30.0 ^{\circ}} k zemskému \boldsymbol{5.00 \ krát 10^{-5} – \textbf{T}} pole. Jaká je síla na 100m úseku této linie? b) diskutovat o případných praktických obavách, které to představuje.
6: Co je síla působící na vodu v MHD jezdit s využitím 25.0 cm-průměr trubice, v případě 100-proud prochází přes trubku, která je kolmá na 2.00-T magnetické pole? (Relativně malá velikost této síly naznačuje potřebu velmi velkých proudů a magnetických polí pro výrobu praktických pohonů MHD.)
7: drát nesoucí 30.0-proud prochází mezi póly silného magnetu, které je kolmé k jeho oboru a zkušenosti 2.16-N platnost 4.00 cm drátu v poli. Jaká je průměrná síla pole?
8: (a) 0.750-m-dlouhý úsek kabelu nesoucí proud na startér auto motor dělá úhlu \boldsymbol{60^{\circ}} Země \boldsymbol{5.50 \times 10^{-5} \;\textbf{T}} pole. Jaký je proud, když drát zažívá sílu \boldsymbol{7.00 \krát 10^{-3} \; \textbf{N}}? (b) Pokud spustíte drátu mezi póly silného podkovy magnet, podrobení 5.00 cm do 1.75-T pole, jaká síla působí na tento segment drátu?
9: (a) Jaký je úhel mezi dráty nesoucí 8.00-aktuální a 1.20-T pole je v případě 50.0 cm drátu zkušenosti magnetické síly 2,40 N? (b) jaká je síla na drátu, pokud se otáčí, aby se úhel \boldsymbol{90^{\circ}} s polem?
10: síla na obdélníkové smyčce drátu v magnetickém poli na obrázku 8 může být použita k měření intenzity pole. Pole je rovnoměrné a rovina smyčky je kolmá k poli. (a) jaký je směr magnetické síly na smyčce? Odůvodněte tvrzení, že síly na stranách smyčky jsou stejné a opačné, nezávisle na tom, kolik smyčky je v poli a neovlivňují čistou sílu na smyčce. (b) je-li použit proud 5,00 A, jaká je síla na Teslu na smyčce široké 20,0 cm?
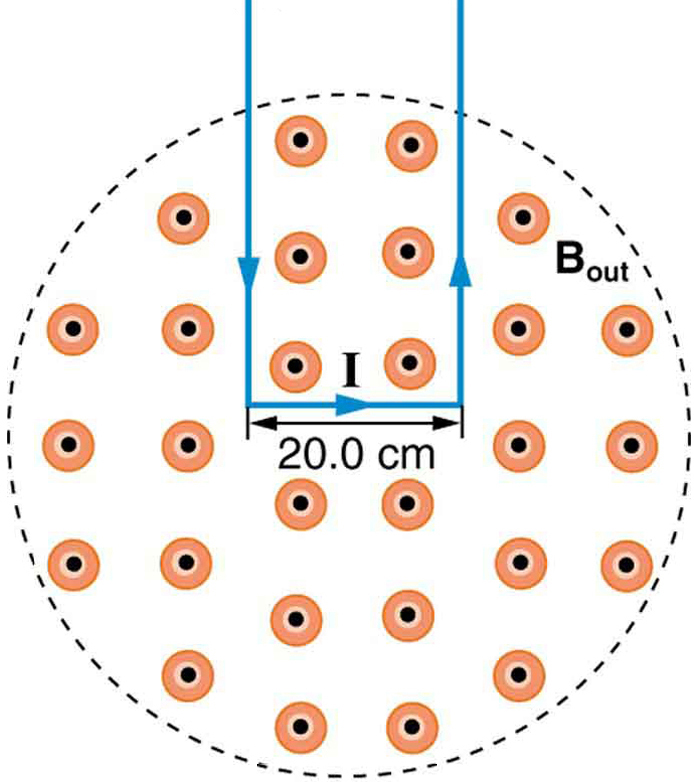
Řešení
Problémy & Cvičení
1: (a) západ (vlevo)
(b) do stránky
(c) na sever (nahoru)
(d) žádná síla,
(e), východ (vpravo)
(f) na jih (dolů)
3: (a) na stránce
(b) západ (vlevo)
(c) ven ze stránky
5: (a) 2.50 N
(b) To je o půl kila síly na 100 m drátu, což je mnohem méně, než je hmotnost drátu samotného. Proto nezpůsobuje žádné zvláštní obavy.
7: 1, 80 T
9: (a) \boldsymbol{30^{\circ}}
(b) 4.80 N
Leave a Reply