Articles

College-Physik

by admin

Zusammenfassung

  • Beschreiben Sie die Auswirkungen einer magnetischen Kraft auf einen stromführenden Leiter.
  • Berechnen Sie die Magnetkraft auf einen stromführenden Leiter.

Da Ladungen normalerweise einem Leiter nicht entweichen können, wird die Magnetkraft auf Ladungen, die sich in einem Leiter bewegen, auf den Leiter selbst übertragen.

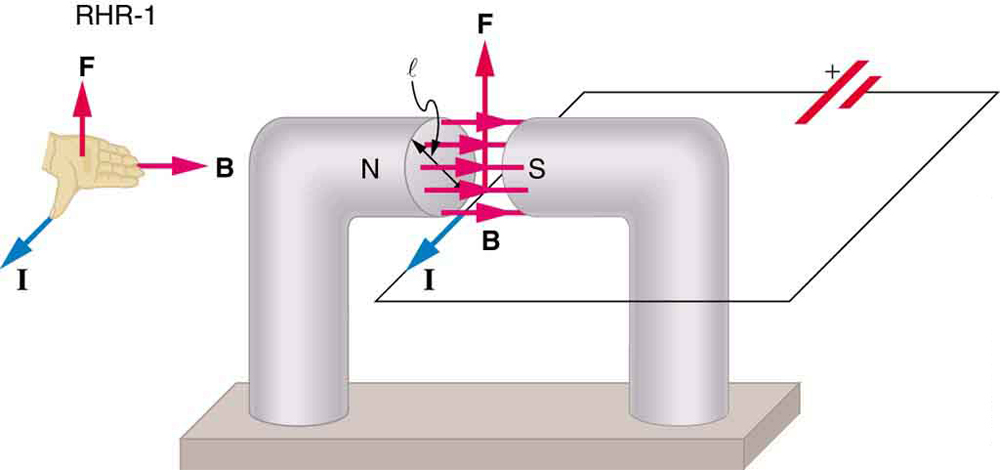
Ein Diagramm, das einen Stromkreis zeigt, durch den Strom I fließt. Ein Abschnitt des Drahtes verläuft zwischen dem Nord- und Südpol eines Magneten mit einem Durchmesser l. Das Magnetfeld B ist nach rechts ausgerichtet, vom Nord- zum Südpol des Magneten, über den Draht. Der Strom läuft aus der Seite. Die Kraft auf den Draht ist nach oben gerichtet. Eine Illustration der rechten Handregel 1 zeigt den Daumen, der aus der Seite in Richtung des Stroms zeigt, die Finger zeigen nach rechts in Richtung B, und der F-Vektor zeigt nach oben und von der Handfläche weg.
Abbildung 1. Das Magnetfeld übt eine Kraft auf einen stromführenden Draht in einer Richtung aus, die durch die rechte Regel 1 gegeben ist (die gleiche Richtung wie die auf die einzelnen beweglichen Ladungen). Diese Kraft kann leicht groß genug sein, um den Draht zu bewegen, da typische Ströme aus einer sehr großen Anzahl bewegter Ladungen bestehen.

Wir können einen Ausdruck für die magnetische Kraft auf einen Strom ableiten, indem wir eine Summe der magnetischen Kräfte auf einzelne Ladungen nehmen. (Die Kräfte addieren sich, weil sie in die gleiche Richtung gehen.) Die Kraft auf eine einzelne Ladung, die sich mit der Driftgeschwindigkeit vdvd bewegt, ist gegeben durch \boldsymbol{F = qv_dB \;\textbf{sin} \;\theta}. Wenn \boldsymbol{B} über eine Drahtlänge \boldsymbol{l} gleichmäßig ist und an anderer Stelle Null ist, ist die gesamte magnetische Kraft auf den Draht dann \boldsymbol{F = (qv_dB \;\textbf{sin} \;\theta) (N)}, wobei \boldsymbol{N} die Anzahl der Ladungsträger in dem Drahtabschnitt der Länge \boldsymbol{l} ist. Nun, \boldsymbol{N=nV} , wobei \boldsymbol{n} die Anzahl der Ladungsträger pro Volumeneinheit und \boldsymbol{V} das Drahtvolumen im Feld ist. Beachten Sie, dass \boldsymbol{V=Al}, wobei \boldsymbol{A} die Querschnittsfläche des Drahtes ist, dann ist die Kraft auf den Draht \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta)(nAl)}. Sammelbegriffe,

\boldsymbol{F=(nqAv_d)lB \;\textbf{sin} \;\theta}.

Weil \boldsymbol{nqAv_d = I} (siehe Kapitel 20.1 Strom),

\boldsymbol{F = IlB \;\textbf{sin} \;\theta}

ist die Gleichung für die magnetische Kraft auf eine Länge \boldsymbol{l} des Drahtes, der einen Strom \boldsymbol{I} in einem boldsymbol{B}, wie in Abbildung 2 gezeigt. Wenn wir beide Seiten dieses Ausdrucks durch \boldsymbol{l} teilen, finden wir, dass die magnetische Kraft pro Längeneinheit des Drahtes in einem gleichförmigen Feld \boldsymbol {\frac{F}{l} = IB \;\textbf{sin} \;\theta} ist. Die Richtung dieser Kraft ist durch RHR-1 gegeben, wobei der Daumen in Richtung des aktuellen \boldsymbol{I} . Dann zeigt mit den Fingern in Richtung \boldsymbol{B} eine Senkrechte zur Handfläche in Richtung \boldsymbol{F}, wie in Abbildung 2.

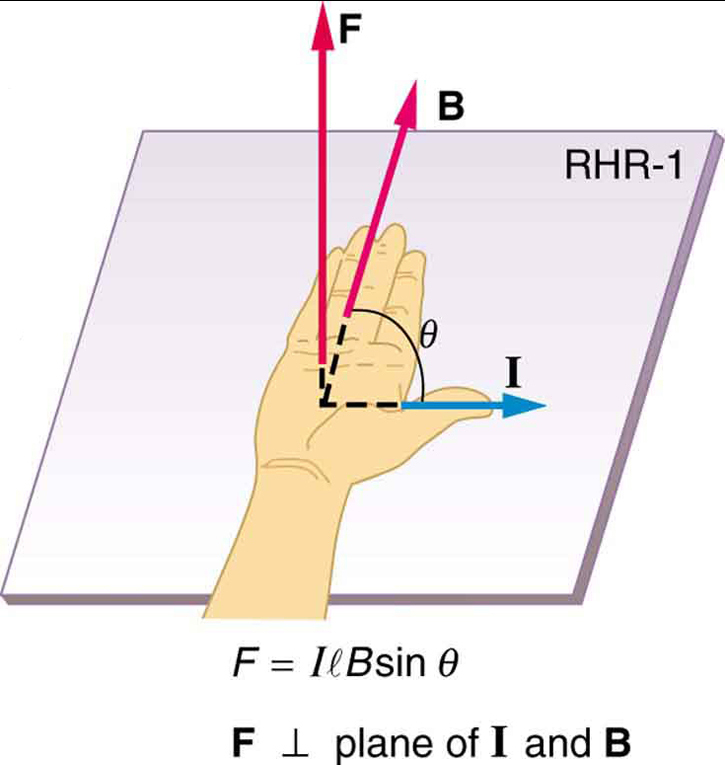
Illustration der Regel 1 für die rechte Hand, die zeigt, dass der Daumen nach rechts in Richtung des Stroms I zeigt, die Finger in die Seite mit dem Magnetfeld B zeigen und die Kraft von der Handfläche weg nach oben gerichtet ist.
Abbildung 2. Die Kraft auf einen stromführenden Draht in einem Magnetfeld ist F = IlB sin θ. Seine Richtung ist durch RHR-1 gegeben.

Berechnung der Magnetkraft auf einem stromführenden Draht: Ein starkes Magnetfeld

Berechnen Sie die Kraft auf den in Abbildung 1 gezeigten Draht mit \boldsymbol{B = 1,50 \;\textbf{T}}, \boldsymbol{l = 5,00 \;\textbf{cm}} und \boldsymbol{I = 20,0 \;\textbf{A}}.

Strategie

Die Kraft kann mit der gegebenen Information gefunden werden, indem man \boldsymbol{F = IlB \;\textbf{sin} \;\theta} verwendet und feststellt, dass der Winkel \boldsymbol{\theta} zwischen \boldsymbol{I} und \boldsymbol{B} \boldsymbol{90 ^{\circ}} ist, so dass \boldsymbol{\textbf{sin} \;\theta = 1} .

Lösung

Eingabe der angegebenen Werte in \boldsymbol{F = IlB \;\textbf{sin} \theta} ergibt

\boldsymbol{F = IlB \;\textbf{sin} \theta = (20.0 \;\textbf{A}) \; (0.0500 \;\textbf{m}) \; (1.50 \;\textbf{T}) \; (1)}.

Die Einheiten für tesla sind \boldsymbol{1 \;\textbf{T} = \frac{\textbf{N}}{\textbf{A} \cdot \; \textbf{m}}}; also

\boldsymbol{F = 1.50 \;\textbf{N}}.

Diskussion

Dieses große Magnetfeld erzeugt eine signifikante Kraft auf eine kleine Drahtlänge.

Die Magnetkraft auf stromführenden Leitern wird verwendet, um elektrische Energie in Arbeit umzuwandeln. (Motoren sind ein Paradebeispiel – sie verwenden Drahtschleifen und werden im nächsten Abschnitt betrachtet.) Magnetohydrodynamik (MHD) ist der technische Name für eine clevere Anwendung, bei der Magnetkraft Flüssigkeiten pumpt, ohne mechanische Teile zu bewegen. (Siehe Abbildung 3.)

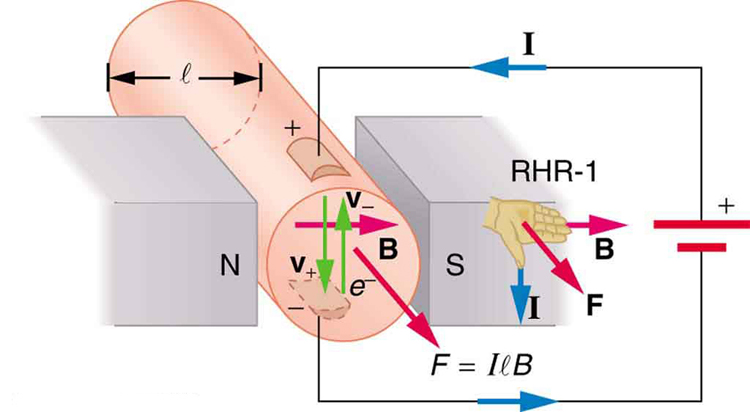
Diagramm, das einen Flüssigkeitszylinder mit dem Durchmesser l zeigt, der zwischen dem Nord- und Südpol eines Magneten angeordnet ist. Der Nordpol ist links. Der Südpol ist rechts. Der Zylinder ist aus der Seite heraus ausgerichtet. Das Magnetfeld ist nach rechts ausgerichtet, vom Nord- zum Südpol und über den Flüssigkeitszylinder. Durch den Fluidzylinder verläuft ein stromführender Draht mit senkrecht zum Zylinder nach unten gerichtetem Strom I. Negative Ladungen innerhalb der Flüssigkeit haben einen Geschwindigkeitsvektor, der nach oben zeigt. Positive Ladungen innerhalb der Flüssigkeit haben einen Geschwindigkeitsvektor, der nach unten zeigt. Die Kraft auf die Flüssigkeit ist aus der Seite. Eine Illustration der rechten Handregel 1 zeigt den Daumen, der mit dem Strom nach unten zeigt, die Finger, die mit B nach rechts zeigen, und die Kraft F, die aus der Seite heraus ausgerichtet ist, weg von der Handfläche.
Abbildung 3. Magnetohydrodynamik. Die Magnetkraft auf den durch diese Flüssigkeit fließenden Strom kann als nichtmechanische Pumpe verwendet werden.

Ein starkes Magnetfeld wird über ein Rohr angelegt und ein Strom wird quer zum Feld durch das Fluid geleitet, was zu einer Kraft auf das Fluid parallel zur Rohrachse führt, wie gezeigt. Das Fehlen beweglicher Teile macht dies attraktiv, um eine heiße, chemisch aktive Substanz wie das in einigen Kernreaktoren eingesetzte flüssige Natrium zu bewegen. Experimentelle Kunstherzen testen mit dieser Technik das Pumpen von Blut und umgehen möglicherweise die nachteiligen Auswirkungen mechanischer Pumpen. (Zellmembranen sind jedoch von den großen Feldern betroffen, die bei MHD benötigt werden, was ihre praktische Anwendung beim Menschen verzögert. Es wurde ein MHD-Antrieb für Atom-U-Boote vorgeschlagen, da er wesentlich leiser sein könnte als herkömmliche Propellerantriebe. Der Abschreckungswert von Atom-U-Booten basiert auf ihrer Fähigkeit, sich zu verstecken und einen ersten oder zweiten Atomschlag zu überleben. Während wir unsere Atomwaffenarsenale langsam zerlegen, wird der U-Boot-Zweig der letzte sein, der aufgrund dieser Fähigkeit außer Dienst gestellt wird (siehe Abbildung 4.) Bestehende MHD-Laufwerke sind schwer und ineffizient — es ist viel Entwicklungsarbeit erforderlich.

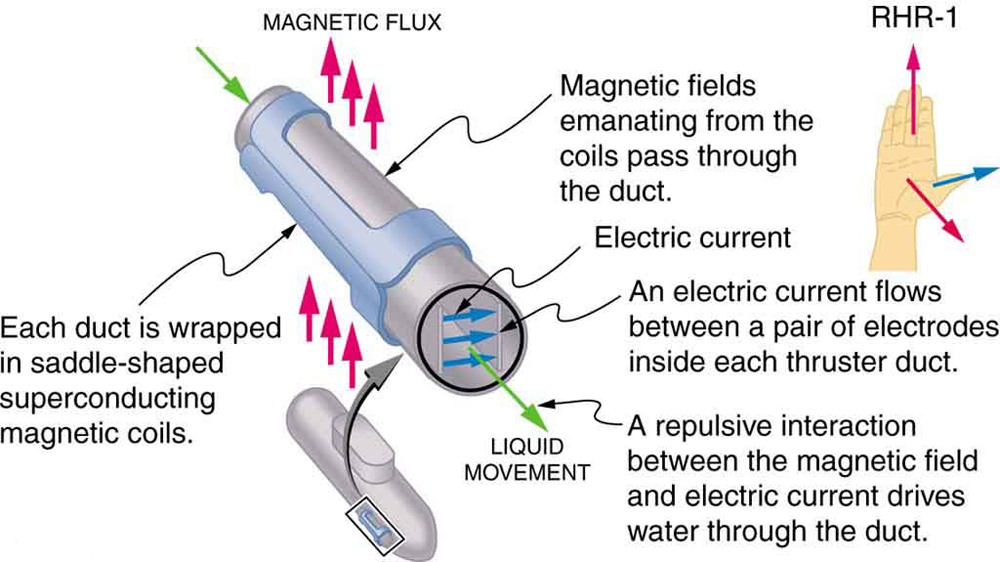
Diagramm, das einen Zoom in ein magnetohydrodynamisches Antriebssystem auf einem Atom-U-Boot zeigt. Flüssigkeit bewegt sich durch den Thrusterkanal, der aus der Seite heraus ausgerichtet ist. Magnetfelder gehen von den Spulen aus und passieren einen Kanal. Der magnetische Fluss ist senkrecht zum Kanal nach oben ausgerichtet. Jeder Kanal ist in sattelförmige supraleitende Spulen gewickelt. Ein elektrischer Strom fließt nach rechts, durch die Flüssigkeit und senkrecht zur Geschwindigkeit der Flüssigkeit. Der elektrische Strom fließt zwischen einem Elektrodenpaar in jedem Triebwerkskanal. Eine abstoßende Wechselwirkung zwischen Magnetfeld und elektrischem Strom treibt Wasser durch den Kanal. Eine Abbildung der rechten Handregel zeigt den Daumen, der mit dem elektrischen Strom nach rechts zeigt. Die Finger zeigen mit dem Magnetfeld nach oben. Die Kraft auf die Flüssigkeit wird von der Seite weg von der Handfläche ausgerichtet.
Abbildung 4. Ein MHD-Antriebssystem in einem Atom-U-Boot könnte deutlich weniger Turbulenzen erzeugen als Propeller und es leiser laufen lassen. Die Entwicklung eines U-Bootes mit leisem Antrieb wurde in dem Buch und dem Film The Hunt for Red October dramatisiert.
  • Die magnetische Kraft auf stromführende Leiter ist gegeben durch
    \boldsymbol{F = IlB \;\textbf{sin} \;\theta},

    wobei \boldsymbol{I} der Strom ist, \boldsymbol{l} die Länge einer geraden \boldsymbol{B} und \boldsymbol{\theta} ist der Winkel zwischen \boldsymbol{I} und \boldsymbol{B}. Die Kraft folgt RHR-1 mit dem Daumen in Richtung \boldsymbol{I}.

Konzeptionelle Fragen

1: Zeichnen Sie eine Skizze der Situation in Abbildung 1, die die Richtung der Elektronen zeigt, die den Strom tragen, und verwenden Sie RHR-1, um die Richtung der Kraft auf den Draht zu überprüfen.

2: Stellen Sie sicher, dass die Richtung der Kraft in einem MHD-Antrieb, wie in Abbildung 3, nicht vom Vorzeichen der Ladungen abhängt, die den Strom durch die Flüssigkeit leiten.

3: Warum sollte ein magnetohydrodynamischer Antrieb im Meerwasser besser funktionieren als im Süßwasser? Warum sollten supraleitende Magnete wünschenswert sein?

4: Was stört eher die Kompasswerte, den Wechselstrom in Ihrem Kühlschrank oder den Gleichstrom, wenn Sie Ihr Auto starten? Erklären.

Probleme & Übungen

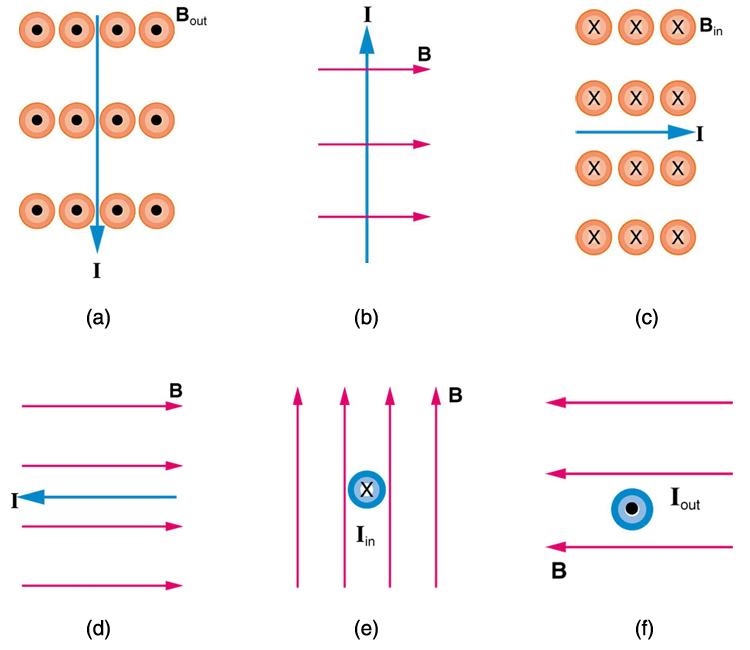
1: Wie ist die Richtung der Magnetkraft auf den Strom in jedem der sechs Fälle in Abbildung 5?

Abbildung a zeigt das Magnetfeld B aus der Seite und den Strom I nach unten. Abbildung b zeigt B nach rechts und I nach oben. Abbildung c zeigt B in die Seite und I nach rechts. Abbildung d zeigt B nach rechts und I nach links. Abbildung e zeigt B nach oben und I in die Seite. Abbildung f zeigt B nach links und I aus der Seite.
Abbildung 5.

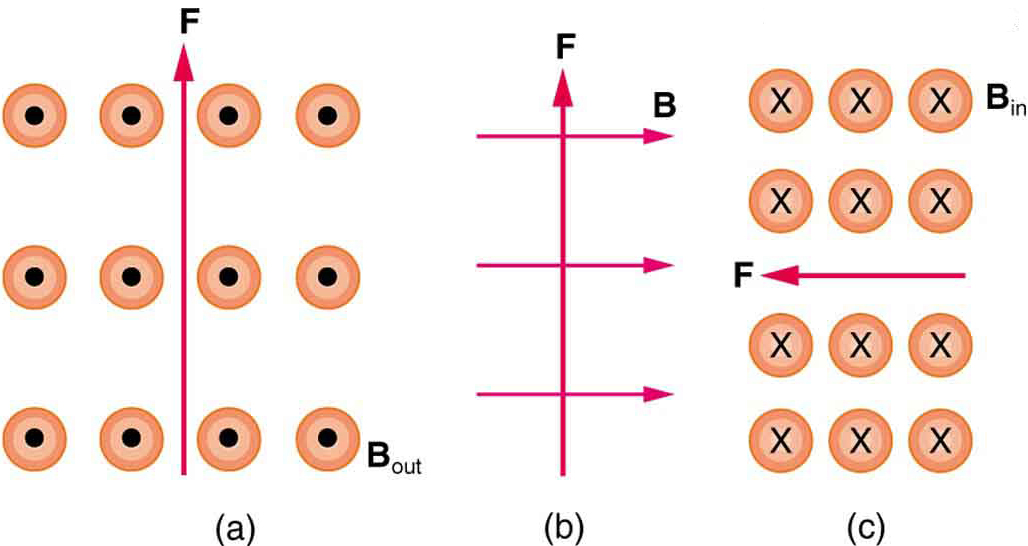
2: In welche Richtung fließt ein Strom, der die in jedem der drei Fälle in Abbildung 6 gezeigte Magnetkraft erfährt, vorausgesetzt, der Strom verläuft senkrecht zu \boldsymbol{B}?

Abbildung a zeigt das Magnetfeld B aus der Seite und die Kraft F nach oben. Abbildung b zeigt B nach rechts und F nach oben. Abbildung c zeigt B in die Seite und F nach links.
Abbildung 6

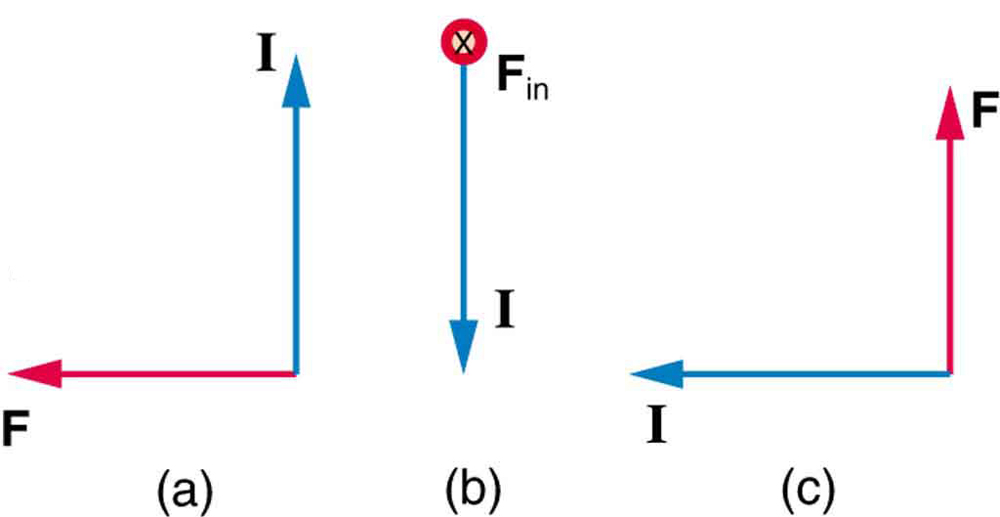
3: Wie ist die Richtung des Magnetfeldes, das die magnetische Kraft erzeugt, die in jedem der drei Fälle in Abbildung 7 auf den Strömen dargestellt ist, vorausgesetzt, \boldsymbol{B} steht senkrecht zu \boldsymbol{I}?

Abbildung a zeigt den aktuellen I-Vektor nach oben und den Kraft F-Vektor nach links. Abbildung b zeigt den aktuellen Vektor nach unten und F in die Seite gerichtet. Abbildung c zeigt die aktuelle zeigt nach links und Kraft nach oben.
Abbildung 7.

4: (a) Was ist die Kraft pro Meter auf einen Blitz am Äquator, der 20.000 A senkrecht zum Feld \boldsymbol{3.00 \times 10^{-5} – \textbf{T}} der Erde trägt? (b) In welche Richtung geht die Kraft, wenn der Strom gerade nach oben fließt und die Feldrichtung der Erde genau nach Norden parallel zum Boden verläuft?

5: (a) Eine Gleichstromleitung für ein Stadtbahnsystem führt 1000 A in einem Winkel von \boldsymbol {30.0 ^ {\circ}} zum \boldsymbol{5.00 \times 10^{-5} – \textbf{T}} Feld der Erde. Was ist die Kraft auf einem 100-m-Abschnitt dieser Linie? (b) Erörtern Sie gegebenenfalls praktische Bedenken.

6: Welche Kraft wird auf das Wasser in einem MHD-Antrieb ausgeübt, der ein Rohr mit einem Durchmesser von 25,0 cm verwendet, wenn 100-A-Strom über das Rohr geleitet wird, das senkrecht zu einem 2,00-T-Magnetfeld steht? (Die relativ geringe Größe dieser Kraft weist auf die Notwendigkeit sehr großer Ströme und Magnetfelder hin, um praktische MHD-Antriebe herzustellen.)

7: Ein Draht, der einen Strom von 30,0 A trägt, fließt zwischen den Polen eines starken Magneten, der senkrecht zu seinem Feld steht, und erfährt eine Kraft von 2,16 N auf den 4,00 cm langen Draht im Feld. Was ist die durchschnittliche Feldstärke?

8: (a) Ein 0,750 m langer Kabelabschnitt, der Strom zu einem Autostarter führt, bildet einen Winkel von \boldsymbol{60^{\circ}} mit dem Feld \boldsymbol{5,50 \times 10^{-5} \;\textbf{T}} der Erde. Was ist der Strom, wenn der Draht eine Kraft von \boldsymbol {7.00 \times 10^{-3} \;\textbf{N}} erfährt? (b) Wenn Sie den Draht zwischen den Polen eines starken Hufeisenmagneten verlegen und 5,00 cm davon einem Feld von 1,75 T aussetzen, welche Kraft wird auf dieses Drahtsegment ausgeübt?

9: (a) Wie groß ist der Winkel zwischen einem Draht, der einen Strom von 8,00 A trägt, und dem Feld von 1,20 T, in dem er sich befindet, wenn 50,0 cm des Drahtes eine Magnetkraft von 2,40 N erfahren? (b) Was ist die Kraft auf den Draht, wenn er gedreht wird, um einen Winkel von \boldsymbol {90 ^ {\circ}} mit dem Feld zu bilden?

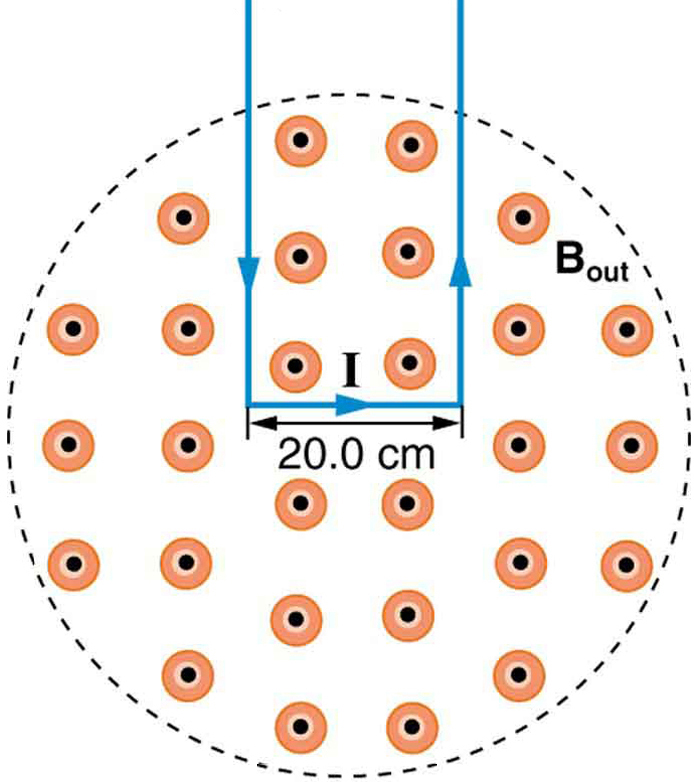
10: Die Kraft auf die rechteckige Drahtschleife im Magnetfeld in Abbildung 8 kann zur Messung der Feldstärke verwendet werden. Das Feld ist gleichmäßig und die Ebene der Schleife steht senkrecht zum Feld. (a) In welche Richtung wirkt die Magnetkraft auf die Schleife? Begründen Sie die Behauptung, dass die Kräfte an den Seiten der Schleife gleich und entgegengesetzt sind, unabhängig davon, wie viel der Schleife sich im Feld befindet, und beeinflussen Sie nicht die Nettokraft auf der Schleife. (b) Wenn ein Strom von 5,00 A verwendet wird, wie hoch ist die Kraft pro Tesla auf der 20,0 cm breiten Schleife?

Diagramm, das eine rechteckige Drahtschleife zeigt, von der sich ein Ende in einem Magnetfeld befindet, das in einem kreisförmigen Bereich vorhanden ist. Das Feld B ist aus der Seite heraus ausgerichtet. Der Strom I verläuft in der Ebene der Seite, auf der linken Seite der Schaltung, nach rechts am unteren Rand der Schaltung und nach oben auf der rechten Seite der Schaltung. Die Länge des Drahtsegments, das am unteren Rand der Schaltung von links nach rechts verläuft, ist zwanzig Zentimeter lang.
Abbildung 8.

Lösungen

Probleme & Übungen

1: (a) West (links)

(b) in Seite

(c) norden (oben)

(d) keine kraft

(e) osten (rechts)

(f) süden (unten)

3: (a) in seite

(b) westen (links)

(c) aus seite

5: (a) 2,50 N

(b) Dies ist etwa ein halbes Pfund Kraft pro 100 m draht, der viel weniger als das Gewicht des Drahtes selbst ist. Daher verursacht es keine besonderen Bedenken.

7: 1,80 Tonnen

9: (a) \boldsymbol{30^{\circ}}

(b) 4,80 N