Articles

Física Universitaria

by admin

Resumen

  • Describir los efectos de una fuerza magnética en un conductor portador de corriente.
  • Calcular la fuerza magnética en un conductor portador de corriente.

Debido a que las cargas normalmente no pueden escapar de un conductor, la fuerza magnética sobre las cargas que se mueven en un conductor se transmite al conductor mismo.

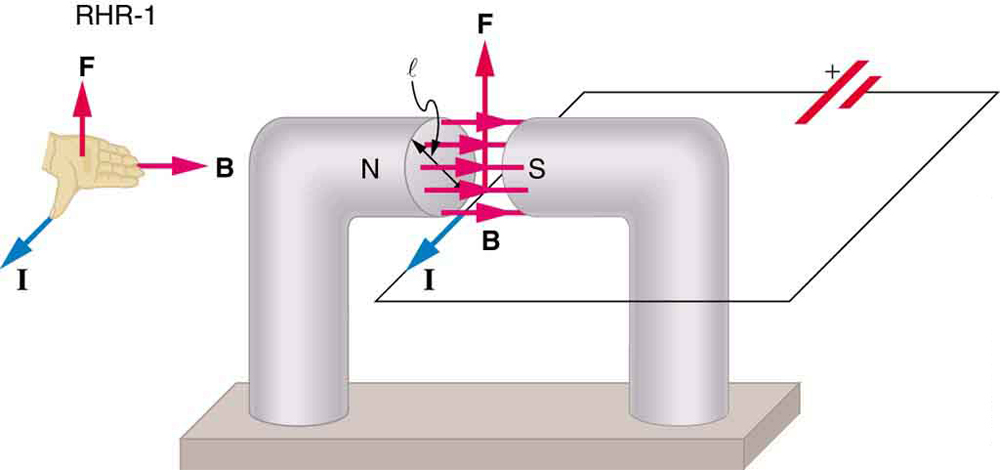
Un diagrama que muestra un circuito con corriente I que pasa a través de ella. Una sección del alambre pasa entre los polos norte y sur de un imán con un diámetro l. El campo magnético B está orientado hacia la derecha, del polo norte al sur del imán, a través del alambre. El actual se agota de la página. La fuerza en el cable se dirige hacia arriba. Una ilustración de la regla 1 de la mano derecha muestra el pulgar apuntando hacia fuera de la página en la dirección de la corriente, los dedos apuntando hacia la derecha en la dirección de B, y el vector F apuntando hacia arriba y lejos de la palma de la mano.
Figura 1. El campo magnético ejerce una fuerza sobre un cable portador de corriente en una dirección dada por la regla 1 de la mano derecha (la misma dirección que la de las cargas móviles individuales). Esta fuerza puede ser lo suficientemente grande como para mover el cable, ya que las corrientes típicas consisten en un gran número de cargas móviles.

podemos derivar una expresión para la fuerza magnética sobre una corriente tomando una suma de las fuerzas magnéticas sobre los derechos individuales. (Las fuerzas se suman porque están en la misma dirección.) La fuerza sobre una carga individual que se mueve a la velocidad de deriva vdvd viene dada por \boldsymbol{F = qv_dB \; \textbf{sin}\; \theta}. Tomando \boldsymbol{B} como uniforme sobre una longitud de cable \boldsymbol{l} y cero en cualquier otro lugar, la fuerza magnética total sobre el cable es entonces \boldsymbol{F = (qv_dB \; \textbf{sin}\; \theta)(N)}, donde \boldsymbol{N} es el número de portadores de carga en la sección de cable de longitud \boldsymbol{l}. Ahora, \boldsymbol{N = nV}, donde \boldsymbol{n} es el número de portadores de carga por unidad de volumen y \boldsymbol{V} es el volumen de cable en el campo. Observando que \boldsymbol{V = Al}, donde \boldsymbol{A} es el área de la sección transversal del cable, entonces la fuerza sobre el cable es \boldsymbol{F = (qv_dB \; \textbf{sin}\; \theta)(nAl)}. Términos de recopilación,

\boldsymbol{F=(nqAv_d)lB \;\textbf{sin} \;\theta}.

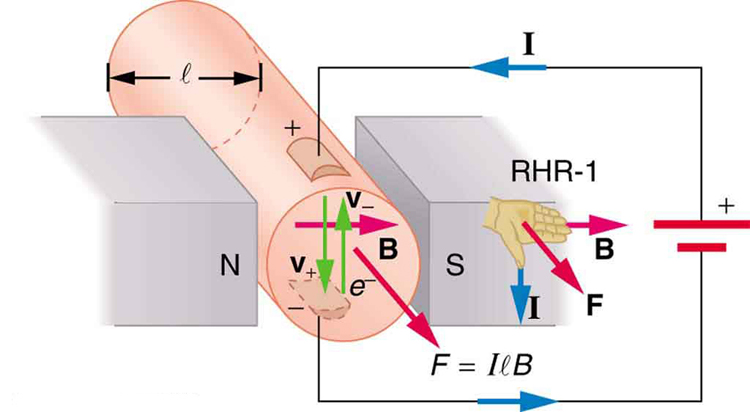
Porque \boldsymbol{nqAv_d = I} (véase el capítulo 20.1 Actual),

\boldsymbol{F = IlB \;\textbf{sin} \;\theta}

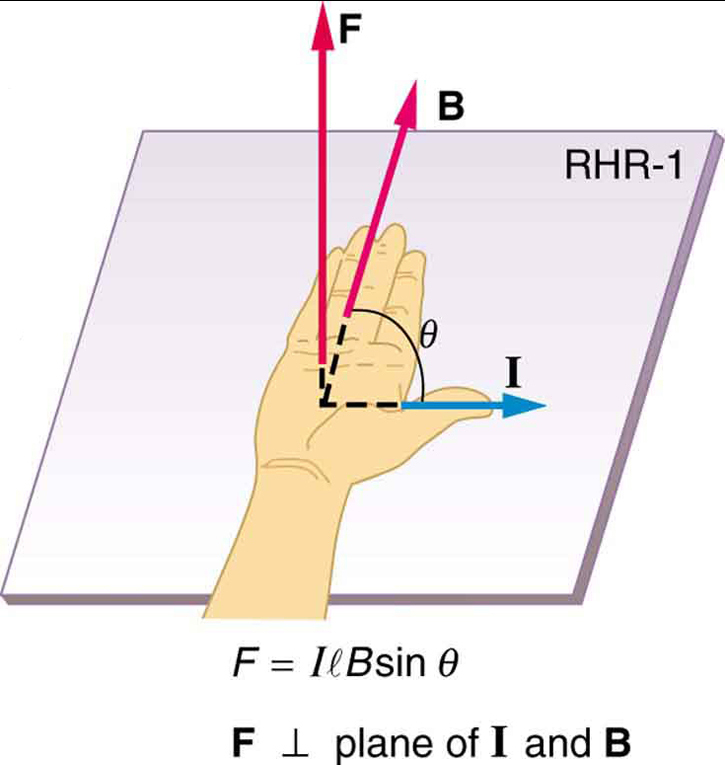
es la ecuación para la fuerza magnética en una longitud \boldsymbol{l} de cable que lleva una corriente \boldsymbol{I} en un campo magnético uniforme \símbolo en bold{B}, como se muestra en la Figura 2. Si dividimos ambos lados de esta expresión por \boldsymbol{l}, encontramos que la fuerza magnética por unidad de longitud de alambre en un campo uniforme es \boldsymbol{\frac {F} {l} = IB \;\textbf{sin}\; \theta}. La dirección de esta fuerza viene dada por RHR-1, con el pulgar en la dirección de la corriente \boldsymbol{I}. Luego, con los dedos en la dirección de \boldsymbol{B}, una perpendicular a la palma apunta en la dirección de \boldsymbol{F}, como en la Figura 2.

Ilustración de la regla 1 de la mano derecha que muestra el pulgar apuntando a la derecha en la dirección de la corriente I, los dedos apuntando a la página con campo magnético B y la fuerza dirigida hacia arriba, lejos de la palma de la mano.
Figura 2. La fuerza en un cable portador de corriente en un campo magnético es F = IlB sin θ. Su dirección está dada por RHR-1.

Calcular la Fuerza Magnética sobre una Corriente-Cable de carga: Un Campo magnético fuerte

Calcula la fuerza sobre el cable que se muestra en la Figura 1, dado \boldsymbol{B = 1.50 \;\textbf{T}}, \boldsymbol{l = 5.00 \;\textbf{cm}}, y \boldsymbol{I = 20.0 \;\textbf{A}}.

Estrategia

La fuerza se puede encontrar con la información dada utilizando \boldsymbol{F = IlB \; \textbf {sin}\; \ theta} y observando que el ángulo \boldsymbol {\theta} entre \boldsymbol{I} y \boldsymbol{B} es \boldsymbol {90 ^{\circ}}, de modo que \boldsymbol {\textbf{sin} \; \ theta = 1}.

Solución

Introducir los valores dados en \boldsymbol{F = IlB \;\textbf{pecado} \theta} rendimientos

\boldsymbol{F = IlB \;\textbf{pecado} \theta = (20.0 \;\textbf{A}) \; (0.0500 \;\textbf{m}) \; (1.50 \;\textbf{T}) \; (1)}.

Las unidades para tesla son \boldsymbol{1 \; \textbf{T} = \frac{\textbf{N}}{\textbf{A} \cdot\; \textbf{m}}}; por lo tanto,

\boldsymbol{F = 1.50\; \textbf{N}}.

Discusión

Este gran campo magnético crea una fuerza significativa en una pequeña longitud de cable.

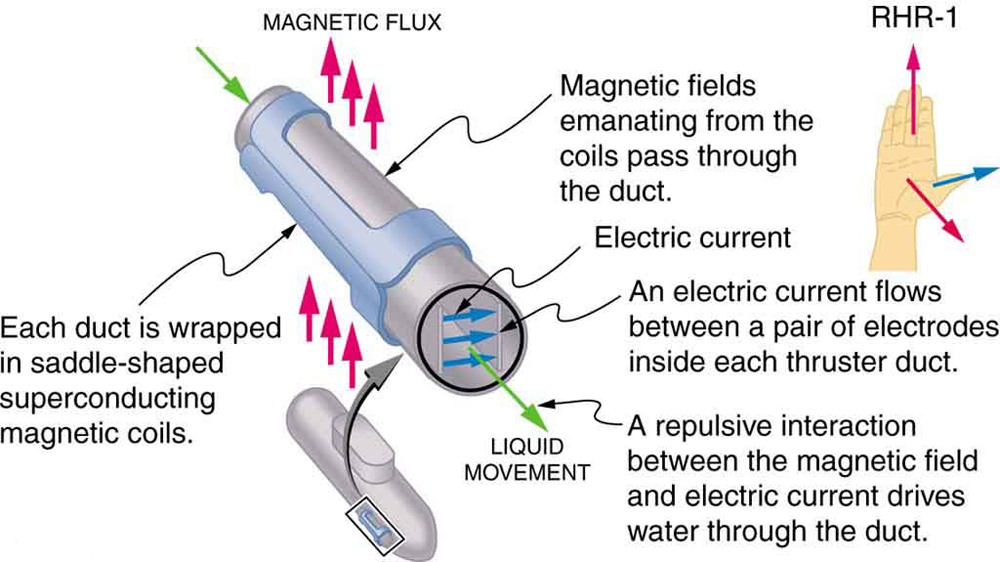
La fuerza magnética en los conductores portadores de corriente se utiliza para convertir la energía eléctrica en trabajo. (Los motores son un buen ejemplo: emplean bucles de alambre y se consideran en la siguiente sección. Magnetohidrodinámica (MHD) es el nombre técnico dado a una aplicación inteligente donde la fuerza magnética bombea fluidos sin mover partes mecánicas. (Véase la Figura 3.)

Diagrama que muestra un cilindro de fluido de diámetro l colocado entre los polos norte y sur de un imán. El polo norte está a la izquierda. El polo sur está a la derecha. El cilindro está orientado fuera de la página. El campo magnético está orientado hacia la derecha, desde el polo norte hasta el polo sur, y a través del cilindro de fluido. Un cable portador de corriente recorre el cilindro de fluido con corriente I orientada hacia abajo, perpendicular al cilindro. Las cargas negativas dentro del fluido tienen un vector de velocidad apuntando hacia arriba. Las cargas positivas dentro del fluido tienen un vector de velocidad apuntando hacia abajo. La fuerza sobre el fluido está fuera de la página. Una ilustración de la regla 1 de la mano derecha muestra el pulgar apuntando hacia abajo con la corriente, los dedos apuntando hacia la derecha con B y forzando la orientación de F hacia fuera de la página, lejos de la palma de la mano.
Figura 3. Magnetohidrodinámica. La fuerza magnética de la corriente que pasa a través de este fluido se puede utilizar como bomba no mecánica.

Se aplica un fuerte campo magnético a través de un tubo y se pasa una corriente a través del fluido en ángulo recto con el campo, lo que resulta en una fuerza en el fluido paralela al eje del tubo, como se muestra. La ausencia de partes móviles lo hace atractivo para mover una sustancia caliente químicamente activa, como el sodio líquido empleado en algunos reactores nucleares. Los corazones artificiales experimentales están probando con esta técnica para bombear sangre, tal vez eludiendo los efectos adversos de las bombas mecánicas. (Las membranas celulares, sin embargo, se ven afectadas por los grandes campos necesarios en MHD, retrasando su aplicación práctica en humanos. Se ha propuesto la propulsión MHD para submarinos nucleares, ya que podría ser considerablemente más silenciosa que los propulsores de hélice convencionales. El valor disuasorio de los submarinos nucleares se basa en su capacidad de esconderse y sobrevivir a un primer o segundo ataque nuclear. A medida que desarmamos lentamente nuestros arsenales de armas nucleares, la rama de submarinos será la última en ser desmantelada debido a esta capacidad (Véase la Figura 4.) Los accionamientos MHD existentes son pesados e ineficientes—se necesita mucho trabajo de desarrollo.

Diagrama que muestra un zoom en magnetohydrodynamic sistema de propulsión en un submarino nuclear. El líquido se mueve a través del conducto del propulsor, que está orientado fuera de la página. Los campos magnéticos emanan de las bobinas y pasan a través de un conducto. El flujo magnético está orientado hacia arriba, perpendicular al conducto. Cada conducto está envuelto en bobinas superconductoras en forma de silla de montar. Una corriente eléctrica corre hacia la derecha, a través del líquido y perpendicular a la velocidad del líquido. La corriente eléctrica fluye entre un par de electrodos dentro de cada conducto del propulsor. Una interacción repulsiva entre el campo magnético y la corriente eléctrica impulsa el agua a través del conducto. Una ilustración de la regla de la mano derecha muestra el pulgar apuntando a la derecha con la corriente eléctrica. Los dedos apuntan hacia arriba con el campo magnético. La fuerza sobre el líquido está orientada fuera de la página, lejos de la palma de la mano.
Figura 4. Un sistema de propulsión MHD en un submarino nuclear podría producir significativamente menos turbulencia que las hélices y permitir que funcionara más silenciosamente. El desarrollo de un submarino silent drive fue dramatizado en el libro y en la película The Hunt for Red October.
  • La fuerza magnética en los conductores portadores de corriente viene dada por
    \boldsymbol{F = IlB \;\textbf{sin} \;\theta},

    donde \boldsymbol{I} es la corriente, \boldsymbol{l} es la longitud de un conductor recto en un campo magnético uniforme \boldsymbol{B}, y \boldsymbol{\theta} es el ángulo entre \boldsymbol{I} y \boldsymbol{B}. La fuerza sigue a RHR – 1 con el pulgar en la dirección de \boldsymbol{I}.

Cuestiones Conceptuales

1: Dibuje un bosquejo de la situación en la Figura 1 que muestra la dirección de los electrones que transportan la corriente, y use RHR-1 para verificar la dirección de la fuerza en el cable.

2: Verifique que la dirección de la fuerza en una unidad MHD, como la de la Figura 3, no dependa del signo de las cargas que transportan la corriente a través del fluido.

3: ¿Por qué un accionamiento magnetohidrodinámico funcionaría mejor en el agua del océano que en el agua dulce? Además, ¿por qué serían deseables los imanes superconductores?

4: ¿Qué es más probable que interfiera con las lecturas de la brújula, la corriente alterna en su refrigerador o la corriente CONTINUA cuando enciende su automóvil? Explicar.

Problemas & Ejercicios

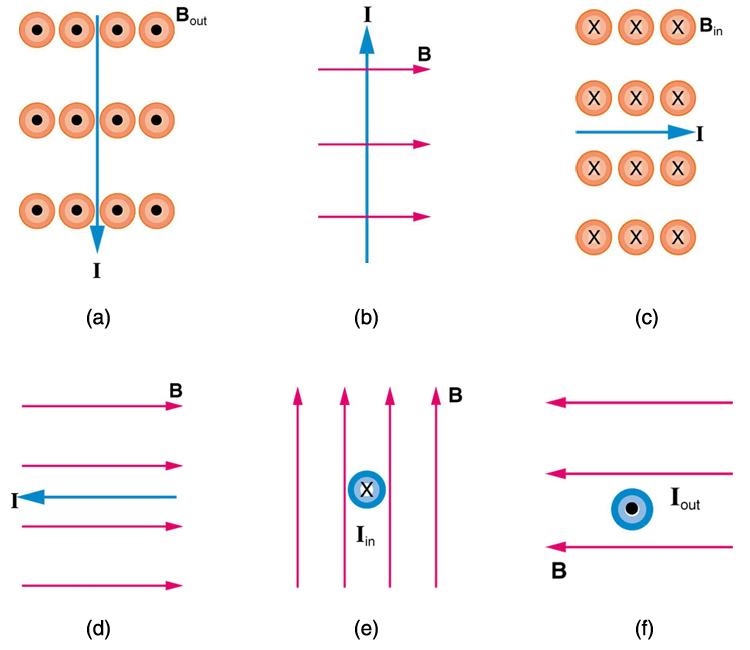
1: ¿Cuál es la dirección de la fuerza magnética en la corriente en cada uno de los seis casos de la Figura 5?

La figura a muestra el campo magnético B fuera de la página y la I actual hacia abajo. La figura b muestra a B hacia la derecha y a I hacia arriba. La figura c muestra B en la página y I hacia la derecha. La figura d muestra B hacia la derecha y I hacia la izquierda. La figura e muestra B hacia arriba y I en la página. La figura f muestra B hacia la izquierda y I fuera de la página.
Figura 5.

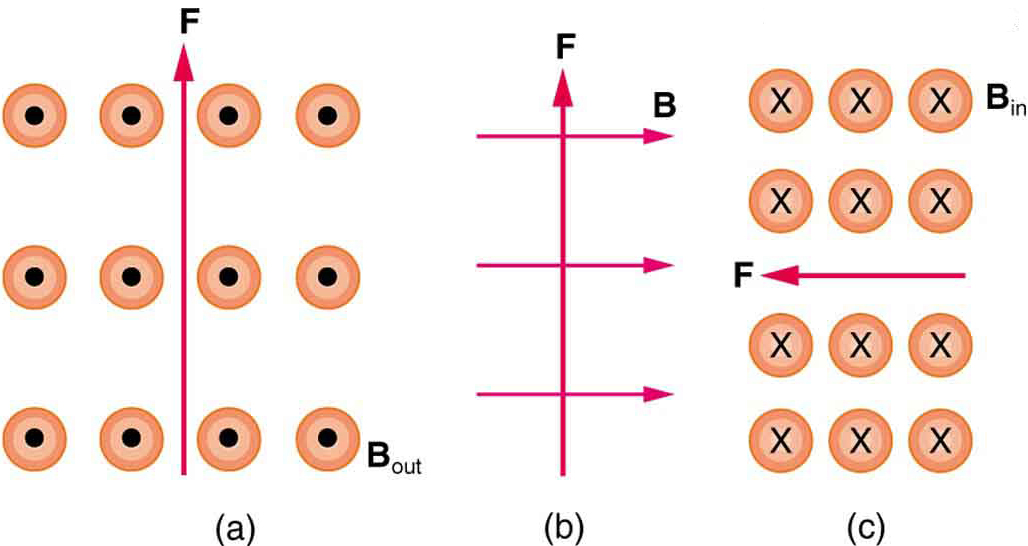
2: ¿Cuál es la dirección de una corriente que experimenta la fuerza magnética mostrada en cada uno de los tres casos de la Figura 6, asumiendo que la corriente corre perpendicular a \boldsymbol{B}?

la Figura a muestra el campo magnético B de la página y la fuerza F hacia arriba. La figura b muestra B hacia la derecha y F hacia arriba. La figura c muestra B en la página y F hacia la izquierda.
Figura 6

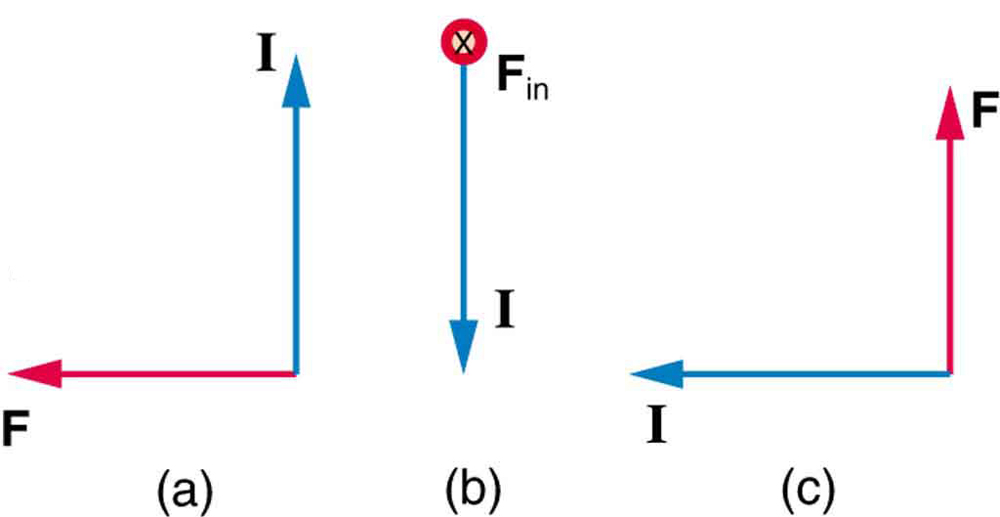
3: ¿Cuál es la dirección del campo magnético que produce la fuerza magnética mostrada en las corrientes en cada uno de los tres casos de la Figura 7, suponiendo que \boldsymbol{B} es perpendicular a \boldsymbol{I}?

La figura a muestra el vector I actual apuntando hacia arriba y el vector F de fuerza apuntando hacia la izquierda. La Figura b muestra el vector actual apuntando hacia abajo y F dirigido a la página. La Figura c muestra la orientación actual hacia la izquierda y la fuerza hacia arriba.
Figura 7.

4: (a) ¿Cuál es la fuerza por metro en un rayo en el ecuador que lleva 20.000 A perpendiculares al campo \boldsymbol{3.00 \times 10^{-5} – \textbf{T}} de la Tierra? (b) ¿Cuál es la dirección de la fuerza si la corriente es recta hacia arriba y la dirección del campo de la Tierra es hacia el norte, paralela al suelo?

5: (a) Una línea de corriente continua para un sistema de carril ligero transporta 1000 A en un ángulo de \boldsymbol{30.0 ^{\circ}} al campo \boldsymbol{5.00 \times 10^{-5}-\textbf{T}} de la Tierra. ¿Cuál es la fuerza en una sección de 100 metros de esta línea? b) Examinar las cuestiones prácticas que ello plantee, si las hubiere.

6: ¿Qué fuerza se ejerce sobre el agua en una unidad MHD que utiliza un tubo de 25,0 cm de diámetro, si se pasa corriente de 100 A a través del tubo perpendicular a un campo magnético de 2,00 T? (El tamaño relativamente pequeño de esta fuerza indica la necesidad de corrientes y campos magnéticos muy grandes para hacer accionamientos MHD prácticos.)

7: Un alambre que lleva una corriente de 30.0-A pasa entre los polos de un imán fuerte que es perpendicular a su campo y experimenta una fuerza de 2.16-N en los 4.00 cm de alambre en el campo. ¿Cuál es la intensidad de campo promedio?

8: (a) Una sección de corriente de transporte de cable de 0,750 m de largo a un motor de arranque de automóvil crea un ángulo de \boldsymbol{60^{\circ}} con el campo \boldsymbol{5,50 \times 10^{-5} \;\textbf{T}} de la Tierra. ¿Cuál es la corriente cuando el cable experimenta una fuerza de \ boldsymbol{7.00 \ times 10^{-3} \;\textbf{N}}? (b) Si pasa el alambre entre los polos de un imán de herradura fuerte, sometiendo 5,00 cm de él a un campo de 1,75 T, ¿qué fuerza se ejerce sobre este segmento de alambre?

9: (a) ¿Cuál es el ángulo entre un cable que transporta una corriente de 8,00 A y el campo de 1,20 T en el que se encuentra si 50,0 cm del cable experimenta una fuerza magnética de 2,40 N? (b) ¿Cuál es la fuerza sobre el cable si se gira para formar un ángulo de \boldsymbol{90^{\circ}} con el campo?

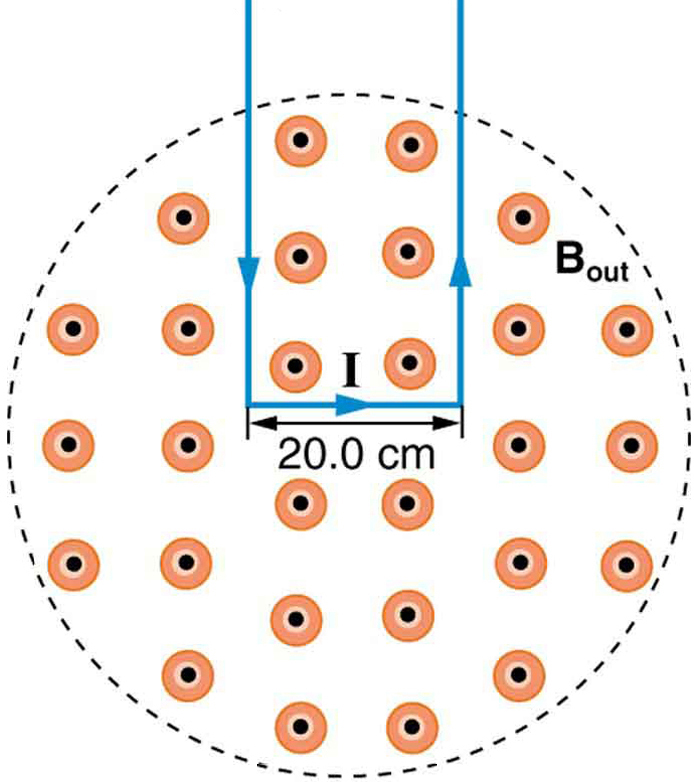
10: La fuerza en el bucle rectangular de alambre en el campo magnético en la Figura 8 se puede usar para medir la intensidad del campo. El campo es uniforme, y el plano del bucle es perpendicular al campo. (a) ¿Cuál es la dirección de la fuerza magnética en el bucle? Justificar la afirmación de que las fuerzas en los lados del bucle son iguales y opuestas, independientemente de la cantidad de bucle que esté en el campo y no afectan a la fuerza neta en el bucle. (b) Si se utiliza una corriente de 5,00 A, ¿cuál es la fuerza por tesla en el bucle de 20,0 cm de ancho?

Diagrama que muestra un bucle rectangular de alambre, un extremo del cual está dentro de un campo magnético que está presente dentro de un área circular. El campo B está orientado fuera de la página. La corriente I corre en el plano de la página, por el lado izquierdo del circuito, hacia la derecha en la parte inferior del circuito, y hacia arriba en el lado derecho del circuito. La longitud del segmento de cable que corre de izquierda a derecha en la parte inferior del circuito es de veinte centímetros de largo.
Figura 8.

Soluciones

Problemas& Ejercicios

1: (a) oeste (izquierda)

(c) norte(arriba)

(d) sin fuerza

(e) este(derecha)

(f) sur(abajo)

3: (a) hacia la página

(b) oeste(izquierda)

(c) fuera de página

5: (a) 2.50 N

(b) Esto es aproximadamente media libra de fuerza por 100 m de cable, que es mucho menor que el peso del cable en sí. Por lo tanto, no causa ninguna preocupación especial.

7: 1.80 T

9: (a) \boldsymbol {30^{\circ}}

(b) 4,80 N