カレッジ物理学
概要
- 電流を運ぶ導体に及ぼす磁力の影響を説明します。
- 電流を流す導体の磁力を計算します。
通常、電荷は導体から逃れることができないため、導体内を移動する電荷に対する磁力は導体自体に伝達されます。p>
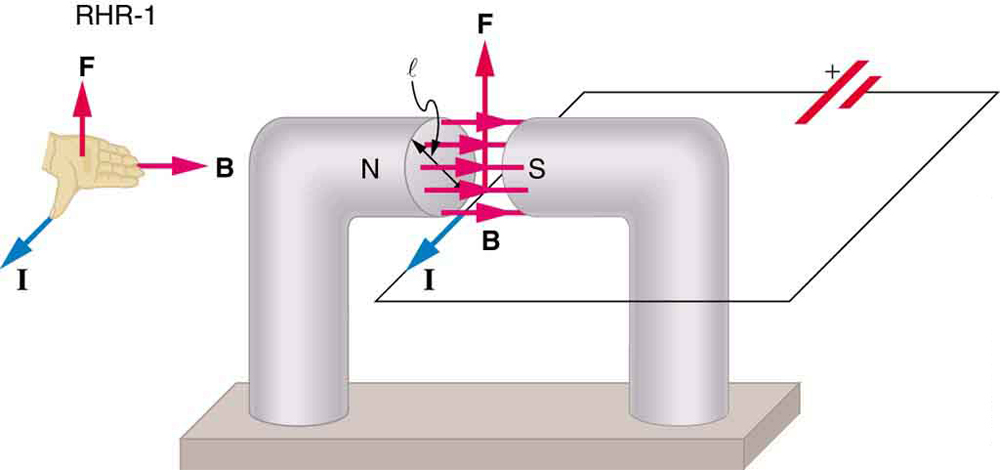
個々の電荷に対する磁力の合計を取ることによって、電流に対する磁力の式を導出することができます。 (力は同じ方向にあるため追加されます。)ドリフト速度vdvdで移動する個々の電荷に対する力は、\boldsymbol{F=qv_db\;\textbf{sin}\;\theta}で与えられます。 \Boldsymbol{B}をワイヤの長さ\boldsymbol{l}にわたって均一にし、他の場所でゼロにすると、ワイヤ上の総磁力は\boldsymbol{F=(qv_db\;\textbf{sin}\;\theta)(N)}になります。\boldsymbol{N}は長さ\boldsymbol{l}のワイヤのセクション内の電荷キャリアの数です。 ここで、\boldsymbol{n}は単位体積あたりの電荷キャリアの数であり、\boldsymbol{V}はフィールド内のワイヤの体積です。\boldsymbol{N=nV}は単位体積あたりの電荷キャリアの数であり、\boldsymbol{V}は ここで、\boldsymbol{A}はワイヤの断面積であり、ワイヤ上の力は\boldsymbol{F=(qv_db\;\textbf{sin}\;\theta)(nAl)}であることに注意してください。 用語を収集する、
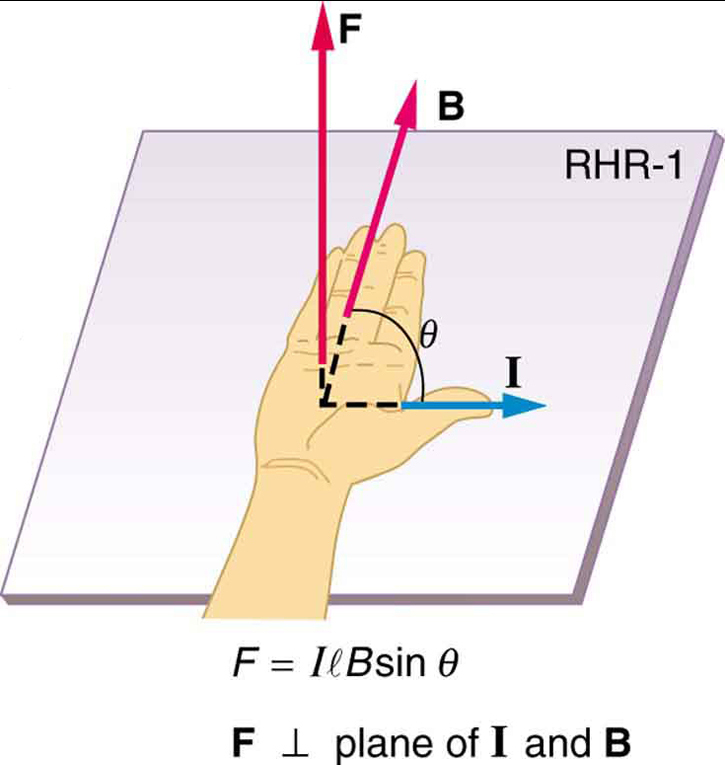
均一な磁場\boldsymbol{I}に電流を運ぶワイヤの長さ\boldsymbol{l}上の磁力の方程式です。\boldsymbol{I}は、均一な磁場\boldsymbol{I}を運ぶワイヤの長さ\boldsymbol{l}上の磁力の方程式です。図2に示すように、{b}。 この式の両側を\boldsymbol{l}で割ると、一様な場におけるワイヤの単位長さあたりの磁力は\boldsymbol{\frac{F}{l}=IB\;\textbf{sin}\;\theta}であることがわかります。 この力の方向はRHR-1によって与えられ、親指は現在の\boldsymbol{I}の方向にあります。 次に、\boldsymbol{B}の方向に指を持つと、手のひらに垂直なaは、図2のように\boldsymbol{F}の方向を指します。
電流を運ぶワイヤの磁力を計算します: 強磁場
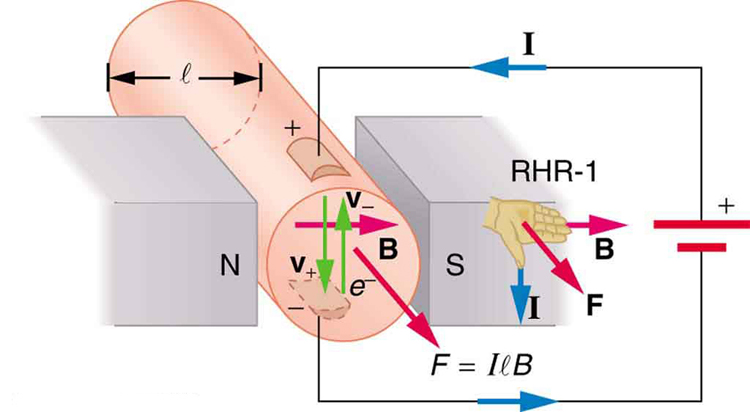
\boldsymbol{B=1.50\;\textbf{T}}、\boldsymbol{l=5.00\;\textbf{cm}}、および\boldsymbol{I=20.0\;\textbf{A}}が与えられたとき、図1に示すワイヤ上の力を計算します。力は、与えられた情報で見つけることができます。\boldsymbol{F=IlB\;\textbf{sin}\;\theta}を使用し、\boldsymbol{I}と\boldsymbol{B}の間の角度\boldsymbol{\theta}が\boldsymbol{90^{\circ}}であることに注意して、\boldsymbol{\textbf{sin}\;\theta=1}。
解
与えられた値を\boldsymbol{F=IlB}に入力します。 \;\textbf{sin}\theta}は
ディスカッション
この大きな磁場は、ワイヤの小さな長さに大きな力を作成します。
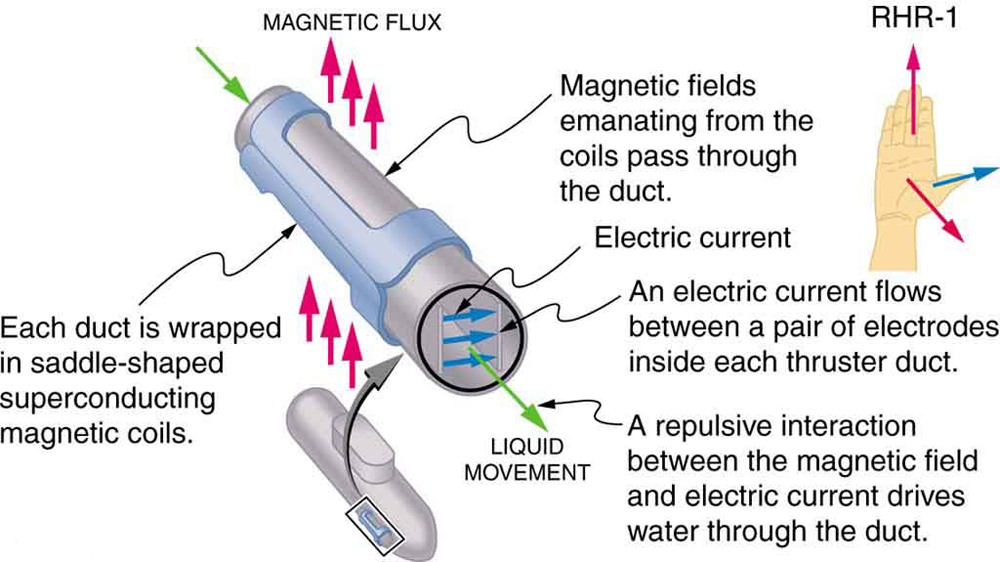
電流を流す導体の磁力は、電気エネルギーを仕事に変換するために使用されます。 (モーターは代表的な例です—彼らはワイヤーのループを採用し、次のセクションで検討されています。)Magnetohydrodynamics(MHD)は磁力が動く機械部品なしで液体をポンプでくむ利発な適用に与えられる技術的な名前である。 (図3を参照してください。)
強い磁場がチューブに印加され、電流がフィールドに直角に流体を通過し、図のようにチューブ軸に平行な流体に力が 可動部品がないため、一部の原子炉で使用されている液体ナトリウムのような、高温で化学的に活性な物質を移動させるのに魅力的です。 実験的な人工心臓は、おそらく機械的ポンプの悪影響を回避するために、血液をポンプするためのこの技術でテストされています。 (しかし、細胞膜はMHDに必要な大きな分野の影響を受け、ヒトでの実用化が遅れている。)原子力潜水艦のためのMHD推進は、従来のプロペラ駆動よりもかなり静かである可能性があるため、提案されている。 原子力潜水艦の抑止力の価値は、第一または第二の核攻撃を隠して生き残る能力に基づいています。 私たちがゆっくりと核兵器を分解するにつれて、潜水艦の支店はこの能力のために最後に廃止されるでしょう(図4を参照)。)既存のMHDドライブは重く、非効率的です-多くの開発作業が必要です。
- 電流を運ぶ導体の磁力は、
\boldsymbol{F=IlB\;\textbf{sin}\;\theta}で与えられます。
ここで、\boldsymbol{I}は電流、\boldsymbol{l}は直線導体の長さですは\boldsymbol{\theta}は\boldsymbol{i}と\boldsymbol{b}の間の角度です。\boldsymbol{\theta}は\boldsymbol{i}と\boldsymbol{b}の間の角度です。 力は\boldsymbol{I}の方向に親指でRHR-1に従います。
概念の質問
1: 電流を運ぶ電子の方向を示す図1の状況のスケッチを描き、RHR-1を使用してワイヤ上の力の方向を確認します。
2:図3のようなMHDドライブの力の方向が、流体を横切って電流を運ぶ電荷の符号に依存しないことを確認します。
3:なぜ磁気流体駆動は淡水よりも海洋水の方がうまくいくのでしょうか? また、なぜ超電導磁石が望ましいのでしょうか?
4
4: あなたの車を始めるときコンパスの読書、あなたの冷却装置またはDCの流れのAC流れと干渉して本当らしいかどれがであるか。 説明しろ
問題&演習
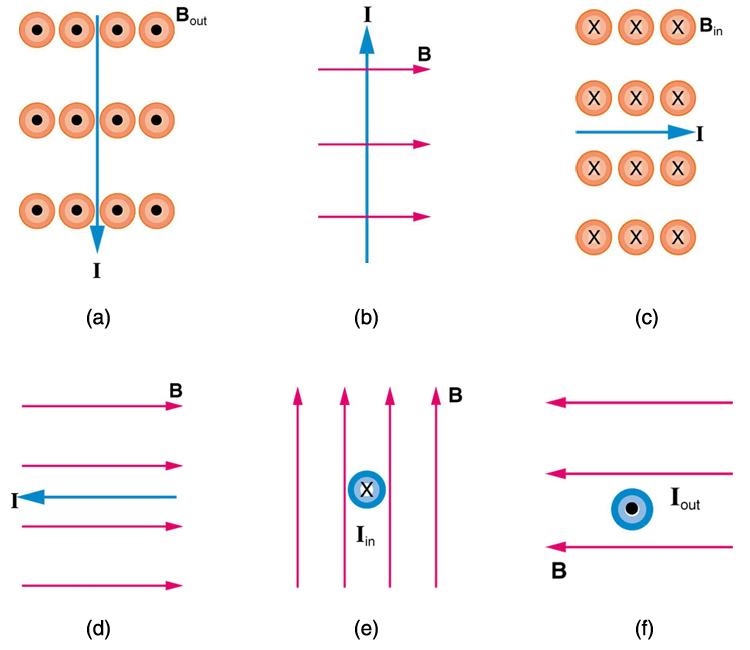
1:図5の6つのケースのそれぞれにおける電流に対する磁力の方向は何ですか?
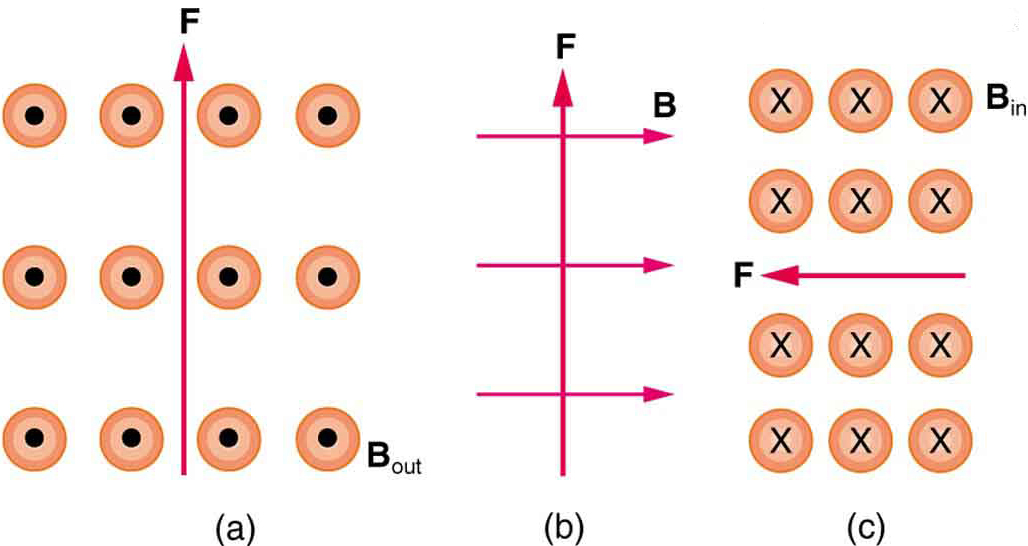
2:電流が\boldsymbol{B}に垂直に走ると仮定して、図6の三つのケースのそれぞれに示す磁力を経験する電流の方向は何ですか?
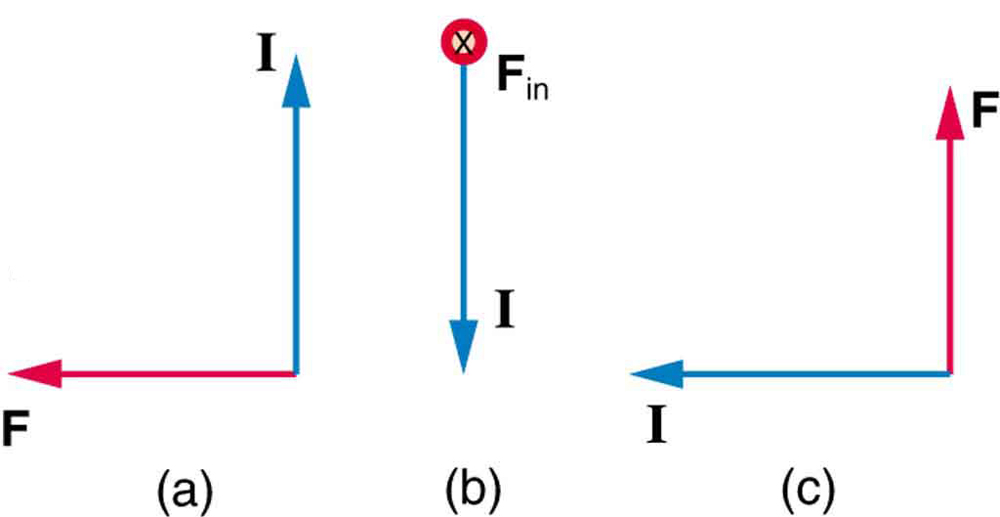
3:\boldsymbol{B}が\boldsymbol{I}に垂直であると仮定して、図7の三つのケースのそれぞれに電流に示す磁力を生成する磁場の方向は何ですか?P>
5
5: (a)ライトレールシステムのDC電力線は、地球の\boldsymbol{5.00\times10^{-5}-\textbf{T}}フィールドに\boldsymbol{30.0^{\circ}}の角度で1000Aを運びます。 このラインの100-mセクションの力は何ですか? (b)もしあれば、これが提示する実用的な懸念について議論する。
6:直径25.0cmのチューブを利用したMHDドライブでは、2.00Tの磁場に垂直なチューブに100Aの電流が流れた場合、水にどのような力がかかりますか? (この力の比較的小さいサイズは、実用的なMHDドライブを作るために非常に大きな電流と磁場が必要であることを示しています。)
7:30.0-a電流を運ぶワイヤは、そのフィールドに垂直であり、フィールド内のワイヤの2.16-nの力を経験する強力な磁石の極の間を通過します4.00cm. 平均電界強度とは何ですか?8:(a)車のスターターモーターに電流を流すケーブルの長さ0.750mの部分は、地球の\boldsymbol{5.50\times10^{-5}\;\textbf{T}}フィールドで\boldsymbol{60^{\circ}}の角度を作ります。 ワイヤが\boldsymbol{7.00\times10^{-3}\;\textbf{N}}の力を経験したときの電流は何ですか? (b)強力な馬蹄形磁石の極の間にワイヤを走らせ、5.00cmを1.75-Tの磁場にかけると、このワイヤのセグメントにどのような力がかかりますか?9:(a)ワイヤの50.0cmが2.40Nの磁力を経験する場合、8.00-aの電流を流すワイヤと1.20-Tの磁場との間の角度は何ですか? (b)フィールドで\boldsymbol{90^{\circ}}の角度を作るために回転させた場合のワイヤの力は何ですか?
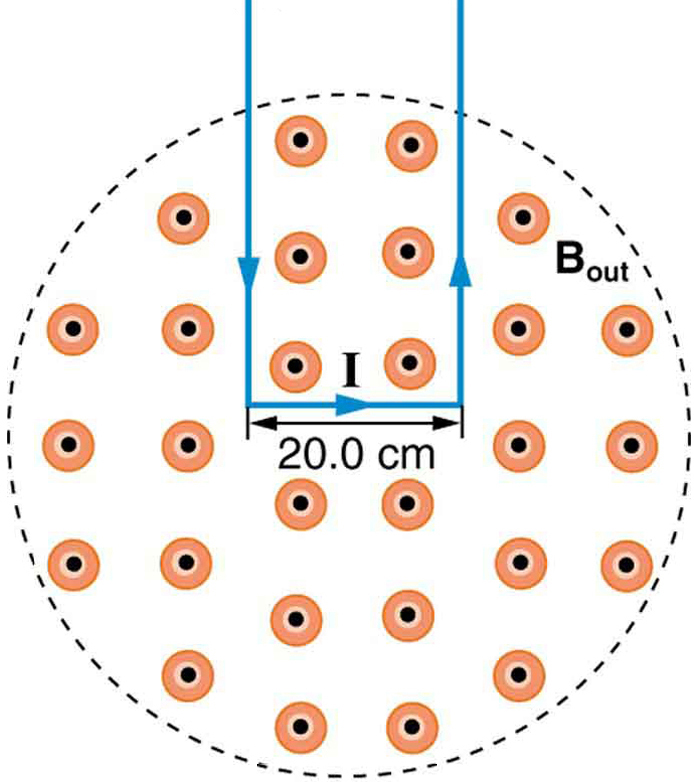
10:図8の磁界中のワイヤの矩形ループ上の力を使用して、電界強度を測定することができます。 場は一様であり、ループの平面は場に対して垂直である。 (a)ループ上の磁力の方向は何ですか? ループの側面の力が等しいと反対であるという主張を正当化し、ループのどのくらいの量がフィールドにあり、ループの正味の力に影響を与えないかとは無関係である。 (b)5.00Aの電流が使用されている場合、20.0cm幅のループのテスラあたりの力はいくらですか?
ソリューション
問題&演習
1:(a)西(左)
(b)ページに
(c)p>
(d)力なし
(e)東(右)
(f)南(下)
3:(a)ページに
(b)西(左)
(c)ページから
5:(a)2.50n
(b)これは、100メートルあたりの力の約半分ポンドですワイヤは、ワイヤ自体の重量よりもはるかに小さい。 したがって、特別な懸念は生じません。
7:1.80T
9: (a)\boldsymbol{30^{\circ}}
(b)4.80N
Leave a Reply