Articles

Collegen fysiikka

by admin

Yhteenveto

  • kuvaa magneettisen voiman vaikutusta virtaa kantavaan johtimeen.
  • laske magneettinen voima virtaa kantavaan johtimeen.

koska varaukset eivät tavallisesti voi paeta johtimesta, johdimessa liikkuviin varauksiin kohdistuva magneettinen voima välittyy johtimeen itseensä.

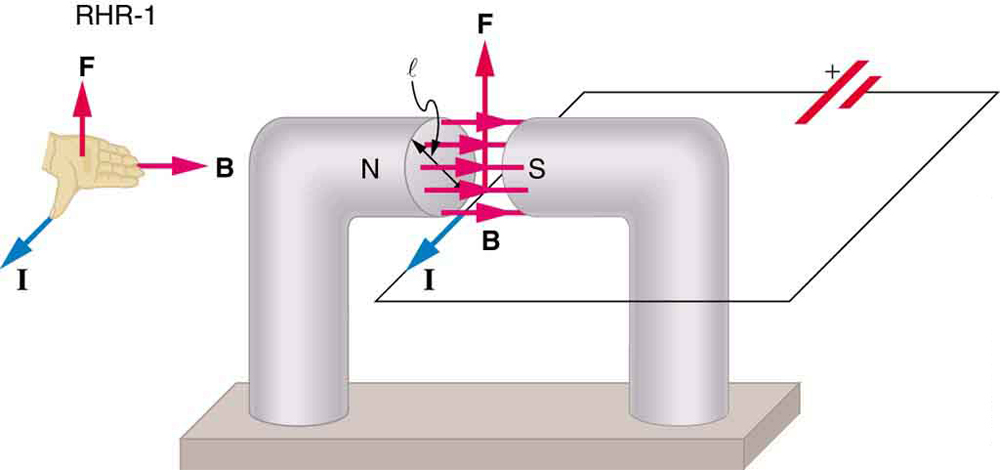
kaavio, joka esittää piiriä, jonka läpi virtaa virta I. Yksi osa johtimesta kulkee halkaisijaltaan l olevan magneetin Pohjois-ja etelänavan välillä. magneettikenttä B suuntautuu johtimen poikki oikealle, pohjoisesta magneetin etelänavalle. Virta loppuu sivulta. Vaijeriin kohdistuva voima kohdistuu ylöspäin. Oikean käden säännön 1 havainnekuvassa peukalo osoittaa sivulta virran suuntaan, sormet osoittavat oikealle B: n suuntaan ja F-vektori osoittaa ylös ja pois kämmenestä.
Kuva 1. Magneettikenttä kohdistaa virtaa kantavaan johtimeen voiman oikean käden säännön 1 antamaan suuntaan (samaan suuntaan kuin yksittäisillä liikkuvilla varauksilla). Tämä voima voi helposti olla tarpeeksi suuri vaijerin liikuttamiseen, koska tyypilliset virrat koostuvat hyvin suurista määristä liikkuvia varauksia.

voidaan johtaa lauseke virran magneettiselle voimalle ottamalla yksittäisten varausten magneettisten voimien summa. (Voimat lisäävät, koska ne ovat samaan suuntaan.) Driftausnopeudella liikkuvaan yksittäiseen varaukseen kohdistuvan voiman vdvd antaa \ boldsymbol{F=qv_dB \; \textbf{sin} \; \theta}. Kun \boldsymbol{B} on yhtenäinen langan pituudella \boldsymbol{l} ja muualla nolla, langan magneettinen kokonaisvoima on tällöin \boldsymbol{F = (qv_dB \;\textbf{sin} \;\theta)(N)}, missä \boldsymbol{n} on varauskantajien lukumäärä langan pituudessa \boldsymbol{l}. Nyt, \boldsymbol{n=nV}, jossa \boldsymbol{n} on varauskantajien lukumäärä tilavuusyksikköä kohti ja \boldsymbol{V} on langan tilavuus kentässä. Huomatessaan, että \boldsymbol{v=Al}, missä \boldsymbol{A} on langan poikkipinta-ala, niin lankaan kohdistuva voima on \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta)(Nal)}. Gathering terms,

\boldsymbol{F=(nqAv_d)lB \;\textbf{sin} \;\theta}.

koska \boldsymbol{Nqav_d = I} (katso luku 20.1 Current),

\boldsymbol{F = IlB \;\textbf{sin} \;\theta}

on yhtälö magneettiselle voimalle pituudella \boldsymbol{l} johtoa, joka kuljettaa virtaa \boldsymbol{I} yhtenäisessä magneettisessa kenttä \boldsymbol{B}, kuten kuvassa 2. Jos jaamme tämän lausekkeen molemmat puolet \boldsymbol{l}: llä, huomaamme, että magneettinen voima langan pituusyksikköä kohti yhtenäisessä kentässä on \boldsymbol{\frac{f}{l} = IB \;\textbf{sin} \;\theta}. Tämän voiman suunnan antaa RHR-1, peukalon ollessa nykyisen \boldsymbolin{I} suunnassa. Sitten sormet suunnassa \boldsymbol{b}, kohtisuorassa kämmen osoittaa suuntaan \boldsymbol{F}, kuten kuvassa 2.

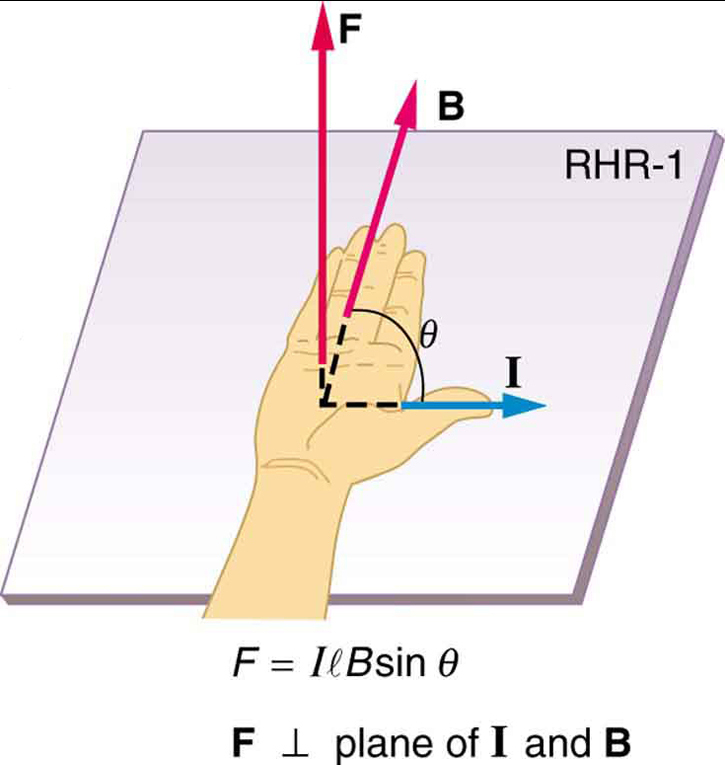
kuvituskuva oikean käden säännöstä 1, jossa peukalo osoittaa oikealle virran I suuntaan, sormet osoittavat sivulle magneettikentän B avulla ja voima suunnataan ylös, poispäin kämmenestä.
kuva 2. Virtaa kantavaan johtimeen kohdistuva voima magneettikentässä on F = IlB sin θ. Sen suunnan antaa RHR-1.

lasketaan magneettista voimaa Virrankantolangalle: Voimakas magneettikenttä

laske langalle kuvassa 1 esitetty voima, kun otetaan huomioon \boldsymbol{b = 1.50 \;\textbf{T}}, \boldsymbol{l = 5.00 \;\textbf{cm}} ja \boldsymbol{I = 20.0 \;\textbf{a}}.

strategia

voima voidaan löytää annetun tiedon avulla käyttämällä \boldsymbol{F = IlB \;\textbf{sin} \;\theta} ja toteamalla, että \boldsymbol{\Theta} \boldsymbol{i} ja \boldsymbol{B} välinen kulma on \boldsymbol{90 ^{\circ}}, joten \boldsymbol{\textbf{sin} \;\theta = 1}.

ratkaisu

annettujen arvojen syöttäminen \boldsymbol{F = IlB \;\textbf{sin} \theta} tuottaa

\boldsymbol{F = IlB \;\textbf{sin} \theta = (20.0 \;\textbf{a}) \; (0.0500 \;\textbf{m}) \; (1.50 \;\textbf{T}) \; (1)}.

Teslan yksiköt ovat \boldsymbol{1 \;\textbf{T} = \frac{\textbf{n}}{\textbf{a} \cdot \; \textbf{m}}}; näin ollen

\boldsymbol{F = 1.50 \;\textbf{n}}.

Keskustelu

Tämä suuri magneettikenttä luo merkittävän voiman pieneen langan pituuteen.

magneettista voimaa virtaa kuljettaviin johtimiin käytetään sähköenergian muuntamiseen työksi. (Moottorit ovat erinomainen esimerkki-ne käyttävät silmukoita lanka ja tarkastellaan seuraavassa osassa.) Magnetohydrodynamiikka (MHD) on tekninen nimitys nokkelalle sovellukselle, jossa magneettinen voima pumppaa nesteitä ilman liikkuvia mekaanisia osia. (KS. Kuva 3.)

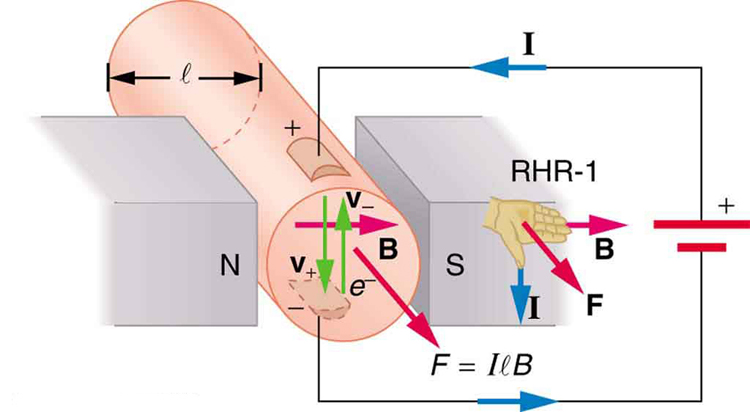
kaavio, jossa läpimitaltaan l oleva nestesylinteri on sijoitettu magneetin Pohjois-ja etelänavan väliin. Pohjoisnapa on vasemmalla. Etelänapa on oikealla. Sylinteri on suunnattu ulos sivulta. Magneettikenttä suuntautuu oikealle, pohjoisesta etelänavalle ja nesteen sylinterin yli. Nestesylinterin läpi kulkee virtaa kantava johto, jonka virta I suuntautuu alaspäin kohtisuoraan sylinteriin nähden. Negatiivisilla varauksilla nesteen sisällä on nopeusvektori, joka osoittaa ylöspäin. Positiivisilla varauksilla on virtausvektori, joka osoittaa alaspäin. Nesteeseen kohdistuva voima on pois sivulta. Oikean käden säännön 1 kuvituksessa peukalo osoittaa alaspäin virralla, sormet osoittavat oikealle B: llä ja voima F suuntautuu sivulta poispäin kämmenestä.
kuva 3. Magnetohydrodynamiikka. Tämän nesteen läpi kulkevan virran magneettista voimaa voidaan käyttää ei-mekaanisena pumppuna.

putken poikki kohdistuu voimakas magneettikenttä ja fluidin läpi kulkee virta suorassa kulmassa kenttään nähden, jolloin fluidiin kohdistuu putken akselin suuntainen voima kuten kuvassa on esitetty. Liikkuvien osien puuttuminen tekee siitä houkuttelevan kuuman, kemiallisesti vaikuttavan aineen, kuten joissakin ydinreaktoreissa käytetyn nestemäisen natriumin, liikuttamiseen. Kokeelliset keinosydämet kokeilevat tällä menetelmällä veren pumppaamista, kenties mekaanisten pumppujen haittavaikutusten kiertämistä. (Solukalvoihin vaikuttavat kuitenkin MHD: ssa tarvittavat suuret kentät, mikä viivästyttää sen käytännön soveltamista ihmisiin.) MHD-propulsiota ydinsukellusveneisiin on ehdotettu, koska se voisi olla huomattavasti hiljaisempi kuin perinteiset potkurikäytöt. Ydinsukellusveneiden pelotearvo perustuu niiden kykyyn piiloutua ja selvitä ensimmäisestä tai toisesta ydiniskusta. Kun vähitellen puramme ydinasearsenaalimme, sukellusvenehaara on viimeinen, joka poistetaan käytöstä tämän kyvyn vuoksi (KS.Kuva 4.) Nykyiset MHD-asemat ovat raskaita ja tehottomia—kehitystyötä tarvitaan paljon.

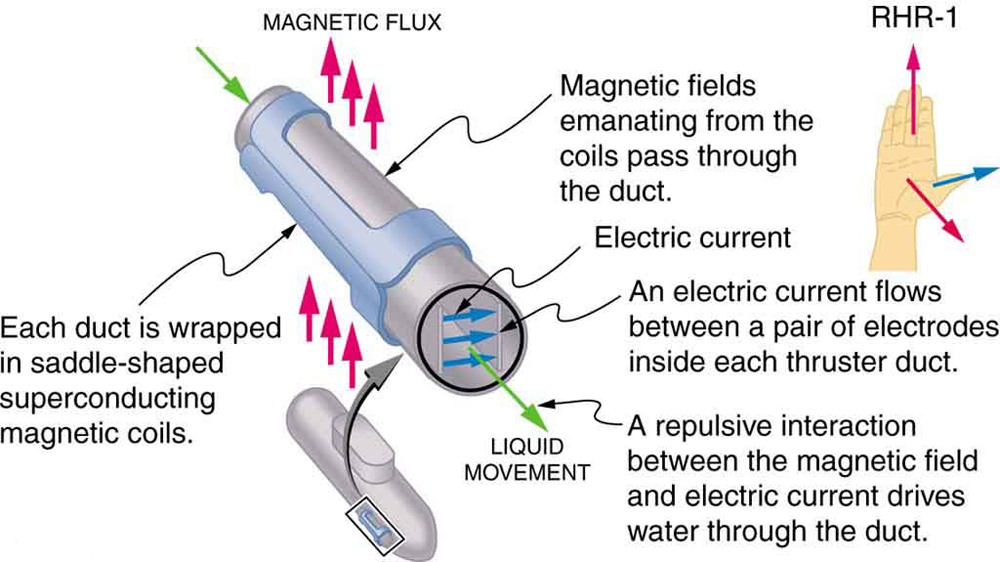
kaavio, jossa zoomataan ydinsukellusveneen magnetohydrodynaamiseen propulsiojärjestelmään. Neste liikkuu työntöpotkurikanavassa, joka on suunnattu ulos sivulta. Magneettikentät lähtevät käämeistä ja kulkevat kanavaa pitkin. Magneettivuo suuntautuu ylöspäin kohtisuoraan kanavaan nähden. Jokainen kanava on kääritty satulan muotoisiin suprajohtaviin keloihin. Sähkövirta kulkee oikealle, nesteen läpi ja kohtisuoraan nesteen nopeuteen nähden. Sähkövirta kulkee elektrodiparin välillä kunkin työntöpotkurikanavan sisällä. Magneettikentän ja sähkövirran välinen vastenmielinen vuorovaikutus ajaa vettä kanavan läpi. Oikean käden säännön havainnekuvassa peukalo osoittaa sähkövirralla oikealle. Sormet osoittavat ylöspäin magneettikentän kanssa. Nesteeseen kohdistuva voima on suunnattu pois sivulta, poispäin kämmenestä.
Kuva 4. Ydinsukellusveneen MHD-propulsiojärjestelmä voisi tuottaa huomattavasti vähemmän turbulenssia kuin potkurit ja antaa sen kulkea äänettömämmin. Silent drive-sukellusveneen kehitystä dramatisoitiin kirjassa ja elokuvassa Punaisen lokakuun metsästys.
  • magneettisen voiman virtaa kantaviin johtimiin antaa
    \boldsymbol{F = IlB \;\textbf{sin} \;\theta},

    missä \boldsymbol{I} on virta, \boldsymbol{l} on suoran johtimen pituus yhtenäisessä magneettikentässä \boldsymbol{B}, ja \boldsymbol{\theta} on kulma \boldsymbol{I}: n ja \boldsymbol{B}: n välillä. Voima seuraa RHR – 1: tä peukalon kanssa \boldsymbolin{i} suuntaan.

käsitteelliset kysymykset

1: Piirrä kaavio Kuvan 1 tilanteesta, jossa esitetään virtaa kuljettavien elektronien suunta, ja käytä RHR-1: tä vahvistaaksesi johdossa olevan voiman suunnan.

2: todennettava, että voiman suunta MHD-voimansiirrossa, kuten kuvassa 3, ei riipu varausten merkistä, joka kuljettaa virtaa nesteen läpi.

3: Miksi magnetohydrodynaaminen voimansiirto toimisi paremmin merivedessä kuin makeassa vedessä? Miksi suprajohtavat magneetit olisivat haluttavia?

4: Kumpi häiritsee todennäköisemmin kompassin lukemia, jääkaapin vaihtovirta vai auton käynnistyessä tasavirta? Selittää.

ongelmat & harjoitukset

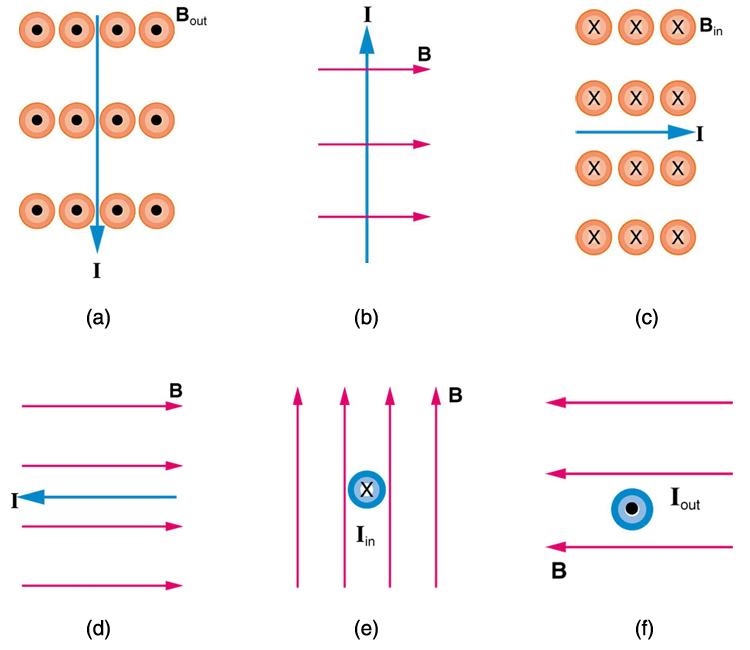
1: Mikä on virran magneettisen voiman suunta kussakin kuvassa 5 esitetyssä kuudessa tapauksessa?

Kuva a näyttää magneettikentän B ulos sivulta ja virran I alaspäin. Kuvassa B näkyy B oikealle ja I ylöspäin. Kuvassa C näkyy B sivulle ja I oikealle. Kuvassa d näkyy B oikealle ja I vasemmalle. Kuvassa e näkyy B ylöspäin ja I sivulle. Kuvassa F näkyy B kohti vasenta ja I pois sivulta.
kuva 5.

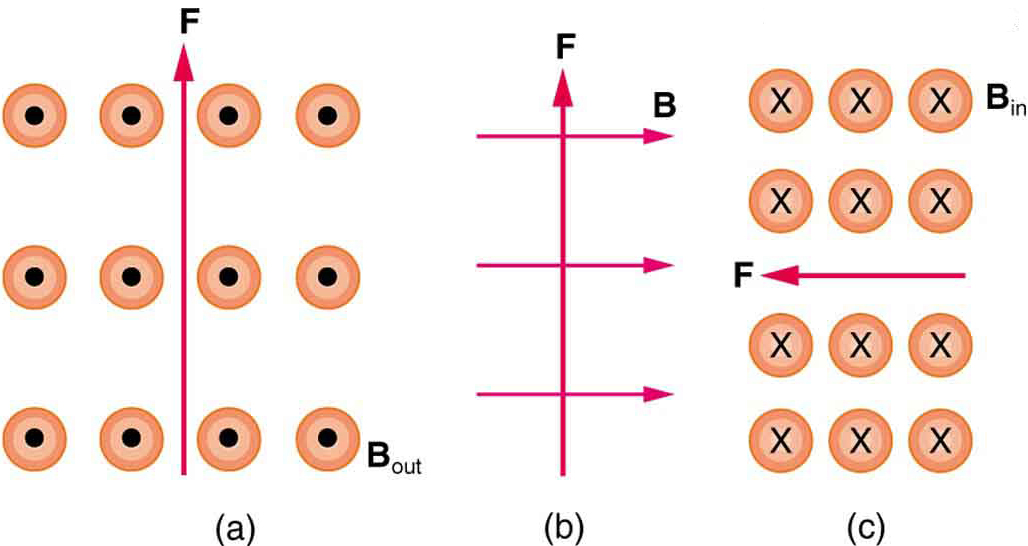
2: Mikä on sellaisen virran suunta, joka kokee magneettisen voiman jokaisessa kuvassa 6 esitetyssä kolmessa tapauksessa olettaen virran kulkevan kohtisuoraan \boldsymbolia{B} vastaan?

Kuva a näyttää magneettikentän B ulos sivusta ja pakottaa F ylöspäin. Kuvassa B näkyy B oikealle ja F ylöspäin. Kuvassa C näkyy B sivulle ja F vasemmalle.
kuva 6

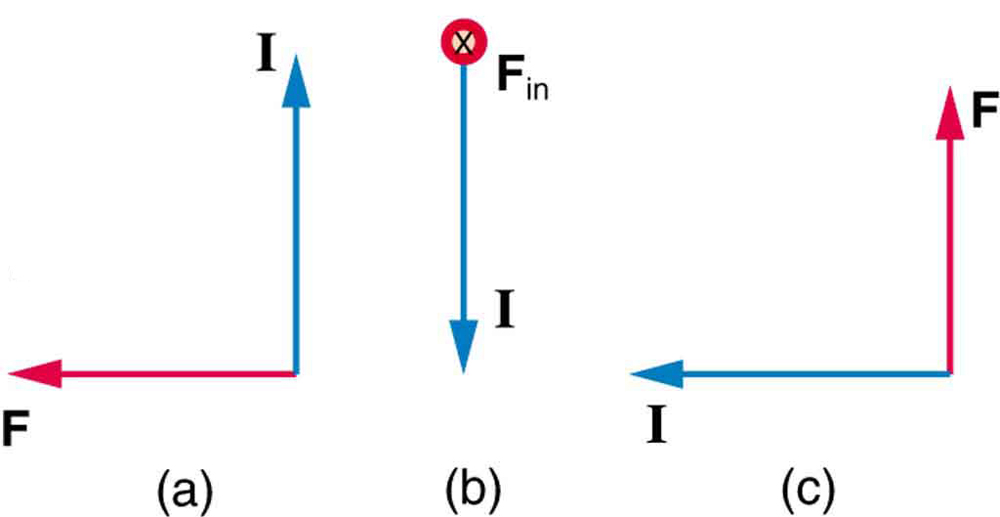
3: Mikä on sen magneettikentän suunta, joka tuottaa virtoihin kohdistuvan magneettisen voiman jokaisessa Kuvan 7 kolmessa tapauksessa, olettaen \boldsymbol{B} on kohtisuorassa \boldsymbol{I}: n kanssa?

Kuva a näyttää nykyisen I vektorin osoittavan ylöspäin ja voiman F vektorin osoittavan vasemmalle. Kuvassa b esitetään nykyinen vektori, joka osoittaa alaspäin ja F suunnataan sivulle. Kuva c näyttää virran osoittavan vasemmalle ja voiman osoittavan ylöspäin.
Kuva 7.

4: A) mikä on se voima metriä kohden päiväntasaajalla salamaniskussa, joka kantaa 20 000 a kohtisuoraan maan \boldsymbol{3.00 \times 10^{-5} – \textbf{T}} kenttää vastaan? b) mikä on voiman suunta, jos virta on suoraan ylöspäin ja maan kenttäsuunta on suoraan pohjoiseen, samansuuntainen maan kanssa?

5: (a) valokiskojärjestelmän TASAVIRTAJOHTO kuljettaa 1000 A: ta \boldsymbol{30.0 ^{\circ}}: n kulmassa maan \boldsymbol{5.00 \times 10^{-5}-\textbf{T}} – kenttään. Mikä on voima 100 metrin rataosuudella? B) keskustele mahdollisista käytännön huolenaiheista.

6: mikä voima kohdistuu veteen MHD-asemassa, jossa käytetään halkaisijaltaan 25,0 cm: n putkea, jos putken poikki kulkee 100-a-virta, joka on kohtisuorassa 2,00-T: n magneettikenttään nähden? (Tämän voiman suhteellisen pieni koko viittaa siihen, että käytännön MHD-asemien tekemiseen tarvitaan hyvin suuria virtauksia ja magneettikenttiä.)

7: vahvan, kenttäänsä nähden kohtisuorassa olevan magneetin napojen välistä kulkee 30,0-a-virtaa kantava vaijeri, joka kokee 2,16-N voiman 4,00 cm: n vaijeriin kentällä. Mikä on kentän keskimääräinen voimakkuus?

8: (a) 0,750 metrin pituinen osa kaapelia, joka kuljettaa virtaa auton käynnistysmoottoriin, muodostaa \boldsymbol{60^{\circ}}-kulman maan \boldsymbol{5,50 \times 10^{-5} \;\textbf{T}}-kentän kanssa. Mikä on virta, kun johto kokee voiman \boldsymbol{7.00 \times 10^{-3} \; \textbf{n}}? b) jos johdat vaijeria voimakkaan hevosenkenkämagneetin napojen väliin ja kohdistat siitä 5,00 cm: n pituisen 1,75-tonnin kentän, niin mikä voima kohdistuu tähän vaijerin osaan?

9: A) mikä on 8,00-a-virtaa kantavan langan ja sen 1,20-T-kentän välinen kulma, jos 50,0 cm johtimesta kokee 2,40 N: n magneettisen voiman? (B) mikä on voima Lanka, jos sitä kierretään tehdä kulma \boldsymbol{90^{\circ}} kanssa kentän?

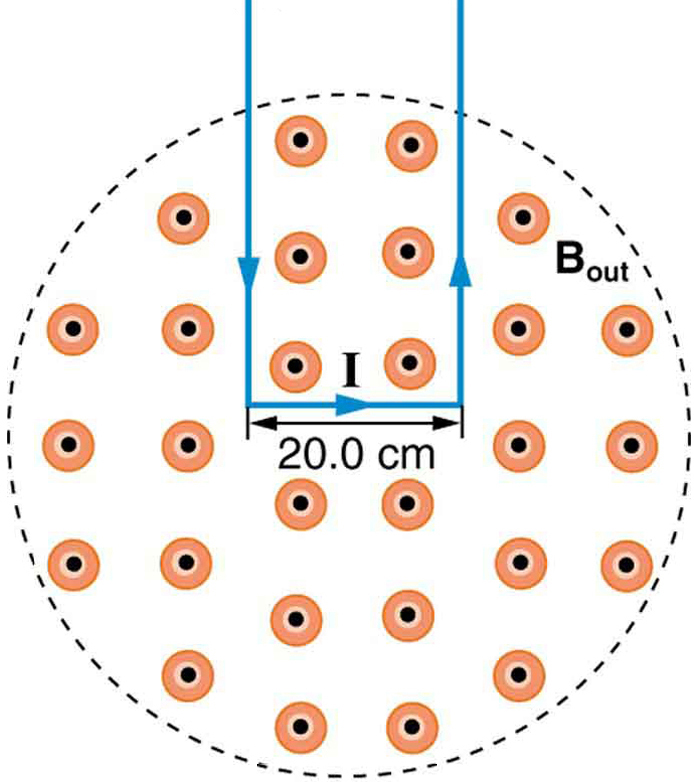
10: kuvan 8 magneettikentässä olevaan suorakaiteen muotoiseen lankasilmukkaan kohdistuvaa voimaa voidaan käyttää kenttävoimakkuuden mittaamiseen. Kenttä on yhtenäinen, ja silmukan taso on kohtisuorassa kenttään nähden. a) mikä on silmukan magneettisen voiman suunta? Perustele väite, että silmukan sivuilla olevat voimat ovat yhtä suuret ja vastakkaiset riippumatta siitä, kuinka suuri osa silmukasta on kentällä, eivätkä vaikuta silmukan nettovoimaan. b) Jos käytetään 5,00 A: n virtaa, mikä on voima Teslaa kohti 20,0 cm leveällä silmukalla?

kaavio, jossa on suorakulmainen lankasilmukka, jonka toinen pää on ympyränmuotoisen alueen sisällä olevassa magneettikentässä. Kenttä B on suunnattu sivun ulkopuolelle. Virta I kulkee tasossa sivun, alas vasemmalla puolella piiri, kohti oikeaa alareunassa piiri, ja ylöspäin oikealla puolella piiri. Piirin alaosassa vasemmalta oikealle kulkevan vaijerin janan pituus on kaksikymmentä senttimetriä.
Kuva 8.

Solutions

Problems &Exercises

1: (A) west (left)

(b) into page

(c) Pohjoinen (ylös)

(D) ei voimaa

(e) Itä (oikealle)

(f) Etelä (alas)

3: (A) sivulle

(b) länteen (vasemmalle)

5: (a) 2,50 n

(b) tämä on noin puoli kiloa voimaa 100 metriä johtoa kohti, mikä on paljon vähemmän kuin itse langan paino. Siksi se ei aiheuta erityisiä huolenaiheita.

7: 1, 80 T

9: (a) \boldsymbol{30^{\circ}}

(b) 4.80 n