Articles

Physique collégiale

by admin

Résumé

  • Décrire les effets d’une force magnétique sur un conducteur porteur de courant.
  • Calculez la force magnétique sur un conducteur porteur de courant.

Comme les charges ne peuvent généralement pas s’échapper d’un conducteur, la force magnétique sur les charges se déplaçant dans un conducteur est transmise au conducteur lui-même.

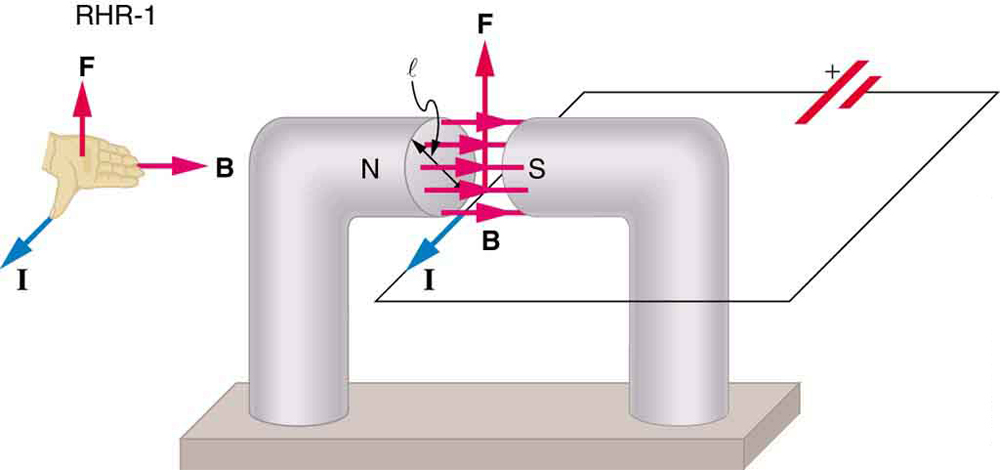
Un diagramme montrant un circuit avec le courant I qui le traverse. Une section du fil passe entre les pôles nord et sud d'un aimant de diamètre l. Le champ magnétique B est orienté vers la droite, du nord au pôle sud de l'aimant, à travers le fil. Le courant sort de la page. La force sur le fil est dirigée vers le haut. Une illustration de la règle de la main droite 1 montre le pouce pointant hors de la page dans la direction du courant, les doigts pointant à droite dans la direction de B, et le vecteur F pointant vers le haut et à l'écart de la paume.
Figure 1. Le champ magnétique exerce une force sur un fil porteur de courant dans une direction donnée par la règle de droite 1 (la même direction que celle des charges mobiles individuelles). Cette force peut facilement être suffisamment importante pour déplacer le fil, car les courants typiques consistent en un très grand nombre de charges mobiles.

Nous pouvons dériver une expression de la force magnétique sur un courant en prenant une somme des forces magnétiques sur des charges individuelles. (Les forces s’ajoutent parce qu’elles sont dans la même direction.) La force sur une charge individuelle se déplaçant à la vitesse de dérive vdvd est donnée par \boldsymbol{F=qv_dB\;\textbf{sin}\;\theta}. En prenant \boldsymbol{B} uniforme sur une longueur de fil \boldsymbol{l} et nulle ailleurs, la force magnétique totale sur le fil est alors \boldsymbol{F =(qv_dB \;\textbf{sin} \;\theta)(N)}, où \boldsymbol{N} est le nombre de porteurs de charge dans la section de fil de longueur \boldsymbol{l}. Maintenant, \boldsymbol {N = nV}, où \boldsymbol {n} est le nombre de porteuses de charge par unité de volume et \boldsymbol {V} est le volume de fil dans le champ. En notant que \boldsymbol {V = Al}, où \boldsymbol{A} est la section transversale du fil, alors la force sur le fil est \boldsymbol{F =(qv_dB \;\textbf{sin} \;\theta)(nAl)}. Les termes de collecte,

\boldsymbol{F=(nqAv_d) lB\;\textbf{sin}\;\theta}.

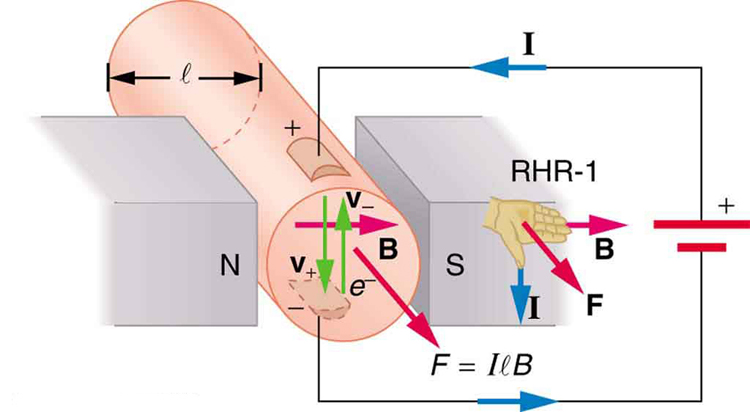
Parce que \boldsymbol{nqAv_d=I} (voir le chapitre 20.1 Courant),

\boldsymbol{F=ILB\;\textbf{sin}\;\theta}

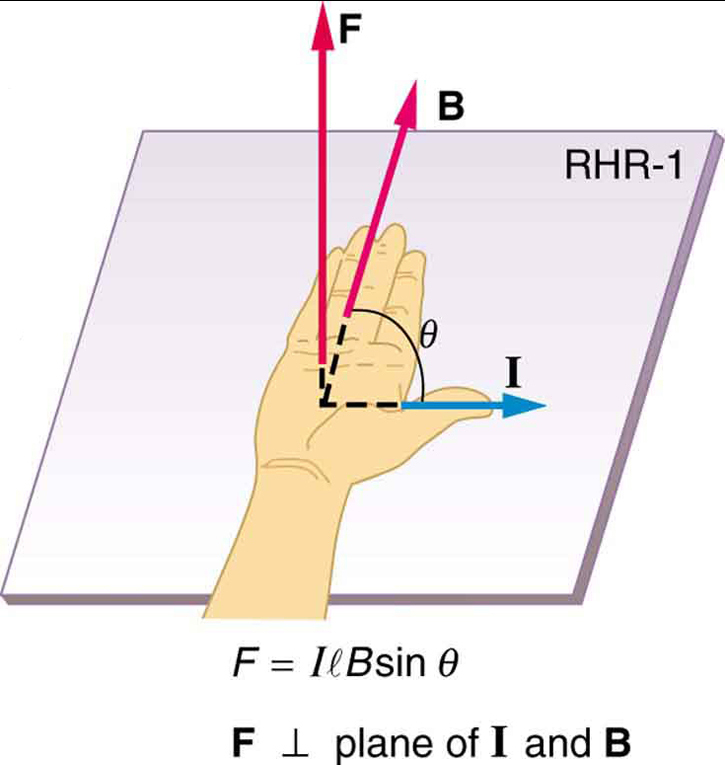
est l’équation de la force magnétique sur une longueur \boldsymbol{l} de fil transportant un courant \boldsymbol{I} dans un champ magnétique uniforme \boldsymbol {B}, comme le montre la figure 2. Si nous divisons les deux côtés de cette expression par \boldsymbol{l}, nous constatons que la force magnétique par unité de longueur de fil dans un champ uniforme est \boldsymbol{\frac{F}{l} = IB\;\textbf{sin}\;\theta}. La direction de cette force est donnée par RHR-1, avec le pouce dans la direction du courant \boldsymbol {I}. Ensuite, avec les doigts dans la direction de \boldsymbol {B}, une perpendiculaire à la paume pointe dans la direction de \boldsymbol {F}, comme sur la figure 2.

Illustration de la règle de la main droite 1 montrant le pouce pointant à droite dans la direction du courant I, les doigts pointant dans la page avec le champ magnétique B et la force dirigée vers le haut, loin de la paume.
Figure 2. La force sur un fil porteur de courant dans un champ magnétique est F = IlB sin θ. Sa direction est donnée par RHR-1.

Calcul de la Force magnétique sur un fil porteur de courant: Un champ magnétique fort

Calculez la force sur le fil illustré à la figure 1, étant donné \boldsymbol{B = 1,50\;\textbf{T}}, \boldsymbol{l = 5,00\;\textbf{cm}}, et \boldsymbol{I = 20,0\;\textbf{A}}.

Stratégie

La force peut être trouvée avec les informations données en utilisant \boldsymbol{F=IlB\;\textbf{sin}\;\theta} et en notant que l’angle \boldsymbol{\theta} entre \boldsymbol{I} et \boldsymbol{B} est \boldsymbol{90^{\circ}}, de sorte que \boldsymbol{\textbf{sin}\;\theta=1}.

Solution

Entrer les valeurs données dans \boldsymbol {F=IlB \;\textbf{sin}\theta} donne

\boldsymbol{F=IlB\;\textbf{sin}\theta=(20.0\;\textbf{A})\;(0.0500\;\textbf{m})\;(1.50\;\textbf{T})\;(1)}.

Les unités pour tesla sont \boldsymbol{1\;\textbf{T}=\frac{\textbf{N}}{\textbf{A}\cdot\;\textbf{m}}}; ainsi,

\boldsymbol{F=1.50\;\textbf{N}}.

Discussion

Ce grand champ magnétique crée une force importante sur une petite longueur de fil.

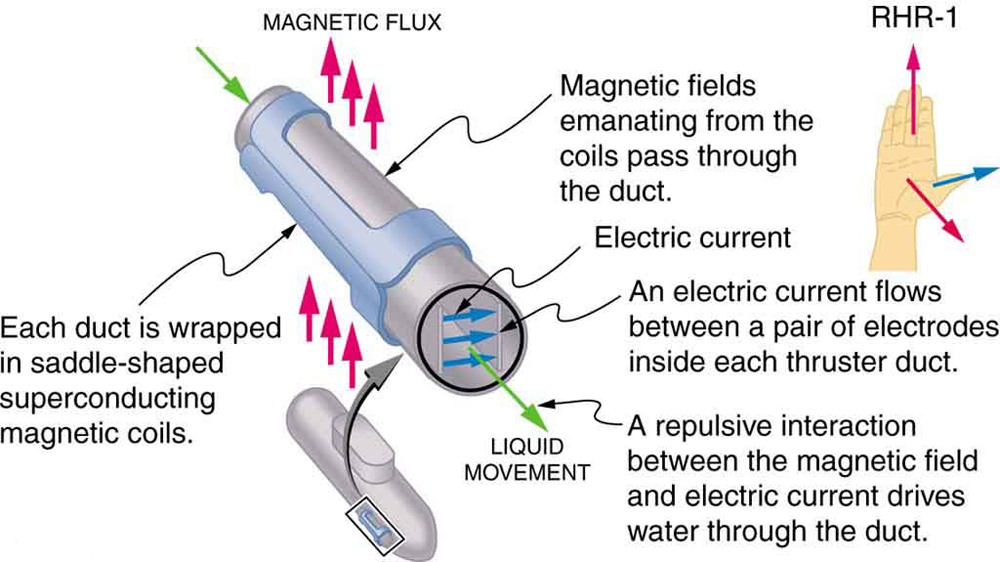
La force magnétique sur les conducteurs porteurs de courant est utilisée pour convertir l’énergie électrique en travail. (Les moteurs sont un excellent exemple — ils utilisent des boucles de fil et sont considérés dans la section suivante.) La magnétohydrodynamique (MHD) est le nom technique donné à une application intelligente où la force magnétique pompe des fluides sans déplacer de pièces mécaniques. (Voir Figure 3.)

Diagramme montrant un cylindre de fluide de diamètre l placé entre les pôles nord et sud d'un aimant. Le pôle nord est à gauche. Le pôle sud est à droite. Le cylindre est orienté hors de la page. Le champ magnétique est orienté vers la droite, du pôle nord au pôle sud, et à travers le cylindre de fluide. Un fil porteur de courant traverse le cylindre de fluide avec le courant I orienté vers le bas, perpendiculairement au cylindre. Les charges négatives dans le fluide ont un vecteur vitesse pointant vers le haut. Les charges positives dans le fluide ont un vecteur vitesse pointant vers le bas. La force sur le fluide est hors de la page. Une illustration de la règle 1 de la main droite montre le pouce pointé vers le bas avec le courant, les doigts pointant vers la droite avec B, et la force F orientée hors de la page, loin de la paume.
Figure 3. Magnétohydrodynamique. La force magnétique sur le courant traversant ce fluide peut être utilisée comme pompe non mécanique.

Un fort champ magnétique est appliqué à travers un tube et un courant traverse le fluide perpendiculairement au champ, ce qui entraîne une force sur le fluide parallèlement à l’axe du tube comme indiqué. L’absence de pièces mobiles le rend attrayant pour déplacer une substance chaude chimiquement active, telle que le sodium liquide utilisé dans certains réacteurs nucléaires. Des cœurs artificiels expérimentaux testent cette technique de pompage du sang, contournant peut-être les effets néfastes des pompes mécaniques. (Les membranes cellulaires, cependant, sont affectées par les grands champs nécessaires à la MHD, ce qui retarde son application pratique chez l’homme.) La propulsion MHD pour les sous-marins nucléaires a été proposée, car elle pourrait être considérablement plus silencieuse que les hélices conventionnelles. La valeur dissuasive des sous-marins nucléaires est basée sur leur capacité à cacher et à survivre à une première ou une deuxième frappe nucléaire. Alors que nous démontons lentement nos arsenaux d’armes nucléaires, la branche des sous-marins sera la dernière à être mise hors service en raison de cette capacité (voir Figure 4.) Les disques MHD existants sont lourds et inefficaces — beaucoup de travail de développement est nécessaire.

Diagramme montrant un zoom avant sur un système de propulsion magnétohydrodynamique sur un sous-marin nucléaire. Le liquide se déplace à travers le conduit du propulseur, qui est orienté hors de la page. Des champs magnétiques émanent des bobines et traversent un conduit. Le flux magnétique est orienté vers le haut, perpendiculairement au conduit. Chaque conduit est enveloppé dans des bobines supraconductrices en forme de selle. Un courant électrique passe à droite, à travers le liquide et perpendiculairement à la vitesse du liquide. Le courant électrique circule entre une paire d'électrodes à l'intérieur de chaque conduit de propulseur. Une interaction répulsive entre le champ magnétique et le courant électrique entraîne l'eau à travers le conduit. Une illustration de la règle de la main droite montre le pouce pointant vers la droite avec le courant électrique. Les doigts pointent vers le haut avec le champ magnétique. La force sur le liquide est orientée hors de la page, loin de la paume.
Figure 4. Un système de propulsion MHD dans un sous-marin nucléaire pourrait produire beaucoup moins de turbulences que les hélices et lui permettre de fonctionner plus silencieusement. Le développement d’un sous-marin à entraînement silencieux a été dramatisé dans le livre et le film La Chasse à Octobre rouge.
  • La force magnétique sur les conducteurs porteurs de courant est donnée par
    \boldsymbol{F=IlB\;\textbf{sin}\;\theta},

    où \boldsymbol{I} est le courant, \boldsymbol{l} est la longueur d’un conducteur droit dans un champ magnétique uniforme \boldsymbol{B}, et \boldsymbol{\theta} est l’angle entre \boldsymbol{I} et \boldsymbol{B}. La force suit RHR-1 avec le pouce dans la direction de \boldsymbol {I}.

Questions conceptuelles

1: Dessinez un croquis de la situation sur la figure 1 montrant la direction des électrons transportant le courant et utilisez RHR-1 pour vérifier la direction de la force sur le fil.

2: Vérifiez que la direction de la force dans un entraînement MHD, tel que celui de la figure 3, ne dépend pas du signe des charges transportant le courant à travers le fluide.

3:Pourquoi un entraînement magnétohydrodynamique fonctionnerait-il mieux dans l’eau de mer que dans l’eau douce? De plus, pourquoi des aimants supraconducteurs seraient-ils souhaitables?

4: Lequel est le plus susceptible d’interférer avec les lectures de la boussole, le courant alternatif dans votre réfrigérateur ou le courant continu lorsque vous démarrez votre voiture? Expliquer.

Problèmes &Exercices

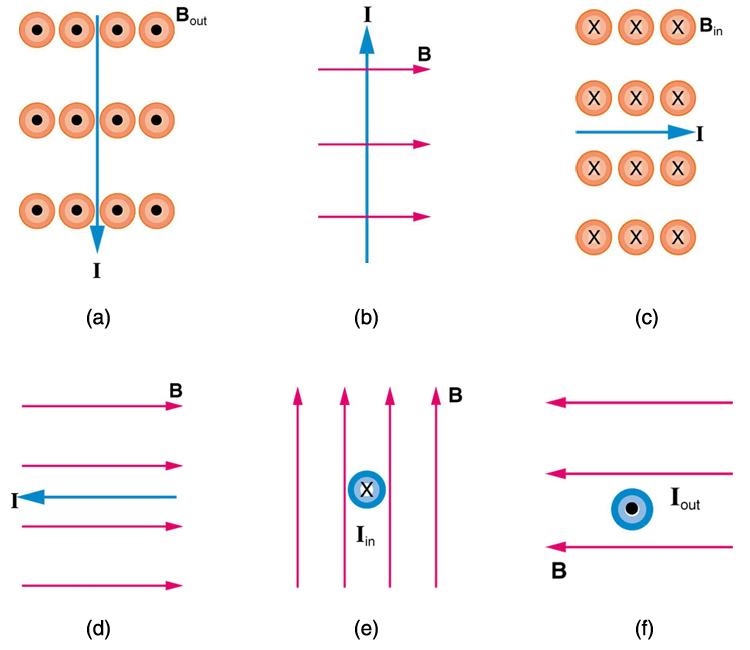
1: Quelle est la direction de la force magnétique sur le courant dans chacun des six cas de la figure 5?

La figure a montre le champ magnétique B hors de la page et le courant I vers le bas. La figure b montre B vers la droite et I vers le haut. La figure c montre B dans la page et I vers la droite. La figure d montre B vers la droite et I vers la gauche. La figure e montre B vers le haut et I dans la page. La figure f montre B vers la gauche et I hors de la page.
Figure 5.

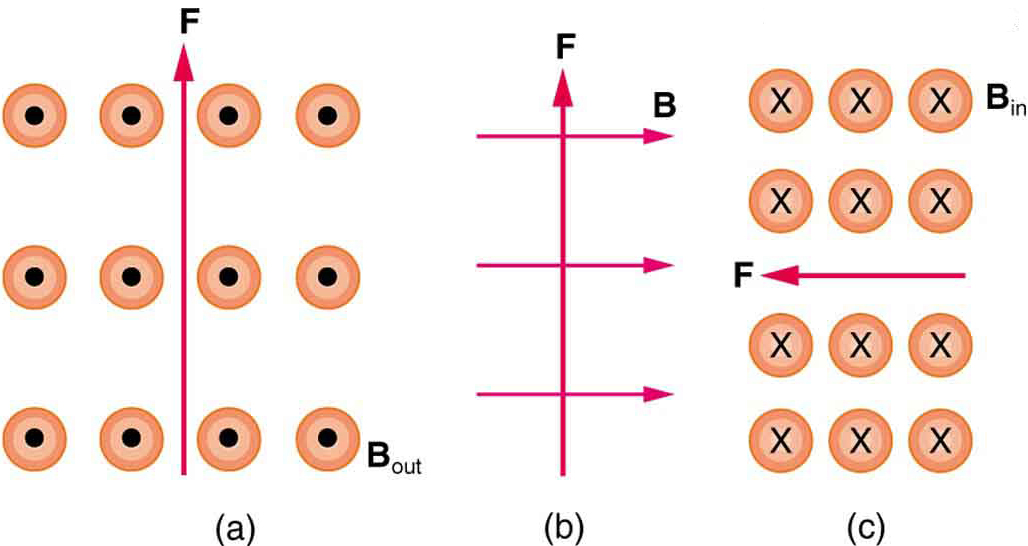
2: Quelle est la direction d’un courant qui subit la force magnétique montrée dans chacun des trois cas de la figure 6, en supposant que le courant passe perpendiculairement à \boldsymbol{B}?

La figure a montre le champ magnétique B hors de la page et force F vers le haut. La figure b montre B vers la droite et F vers le haut. La figure c montre B dans la page et F vers la gauche.
Figure 6

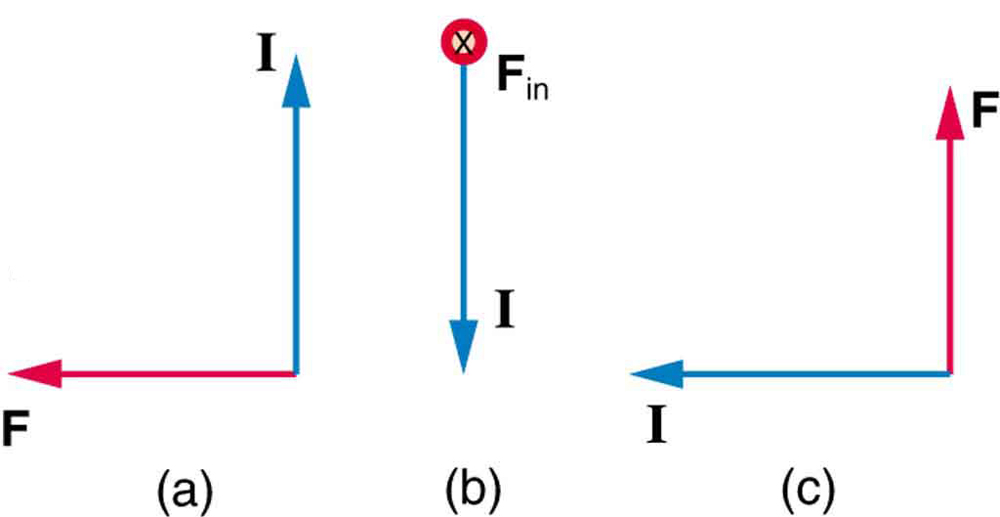
3: Quelle est la direction du champ magnétique qui produit la force magnétique indiquée sur les courants dans chacun des trois cas de la figure 7, en supposant que \boldsymbol{B} est perpendiculaire à \boldsymbol{I}?

La figure a montre le vecteur courant I pointant vers le haut et le vecteur force F pointant vers la gauche. La figure b montre le vecteur courant pointant vers le bas et F dirigé vers la page. La figure c montre le courant pointant vers la gauche et la force pointant vers le haut.
Figure 7.

4:(a) Quelle est la force par mètre sur un éclair à l’équateur qui porte 20 000 A perpendiculairement au champ \boldsymbol{3,00\times 10^{-5}-\textbf{T}}? b) Quelle est la direction de la force si le courant est droit vers le haut et que la direction du champ terrestre est plein nord, parallèle au sol?

5: (a) Une ligne d’alimentation en courant continu pour un système léger sur rail porte 1000 A à un angle de \boldsymbol{30,0^{\circ}} par rapport au champ \boldsymbol{5,00\fois 10^{-5}-\textbf{T}} de la Terre. Quelle est la force sur une section de 100 m de cette ligne? b) Discuter, le cas échéant, des problèmes pratiques que cela présente.

6: Quelle force est exercée sur l’eau dans un entraînement MHD utilisant un tube de 25,0 cm de diamètre, si un courant de 100 A traverse le tube perpendiculairement à un champ magnétique de 2,00 T? (La taille relativement petite de cette force indique la nécessité de très grands courants et champs magnétiques pour réaliser des entraînements MHD pratiques.)

7: Un fil portant un courant de 30,0-A passe entre les pôles d’un aimant fort perpendiculaire à son champ et subit une force de 2,16-N sur les 4,00 cm de fil dans le champ. Quelle est l’intensité de champ moyenne?

8: (a) Une section de câble de 0,750 m de long transportant le courant vers un démarreur de voiture fait un angle de \boldsymbol{60^{\circ}} avec le champ \boldsymbol{5,50\fois 10^{-5}\; \textbf{T}}. Quel est le courant lorsque le fil subit une force de \boldsymbol {7,00\fois 10^{-3} \; \textbf{N}}? (b) Si vous faites passer le fil entre les pôles d’un aimant puissant en fer à cheval, en soumettant 5,00 cm de celui-ci à un champ de 1,75 T, quelle force s’exerce sur ce segment de fil?

9: (a) Quel est l’angle entre un fil transportant un courant de 8,00 A et le champ de 1,20 T dans lequel il se trouve si 50,0 cm du fil subissent une force magnétique de 2,40 N? (b) Quelle est la force sur le fil s’il est tourné pour faire un angle de \boldsymbol{90^{\circ}} avec le champ?

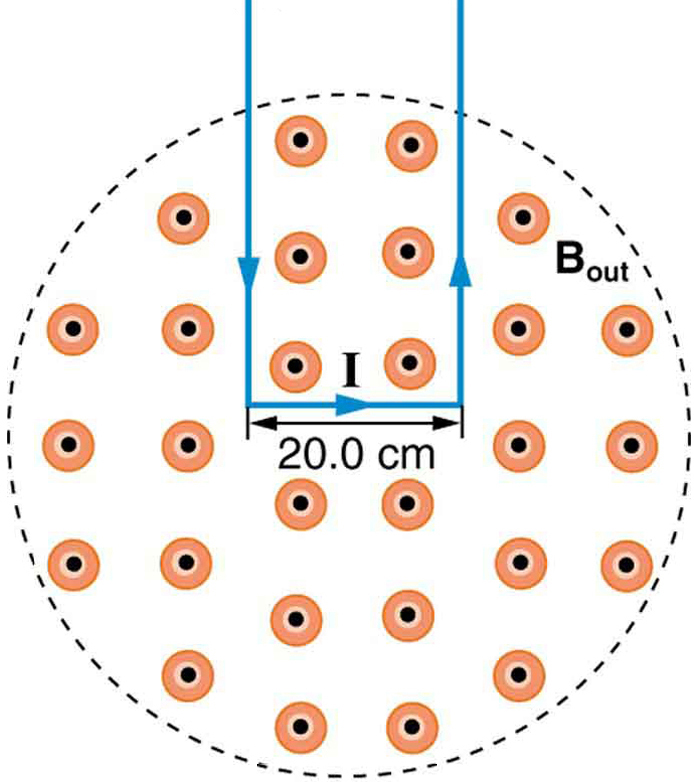
10: La force sur la boucle rectangulaire de fil dans le champ magnétique de la figure 8 peut être utilisée pour mesurer l’intensité du champ. Le champ est uniforme et le plan de la boucle est perpendiculaire au champ. (a) Quelle est la direction de la force magnétique sur la boucle? Justifier l’affirmation selon laquelle les forces sur les côtés de la boucle sont égales et opposées, indépendamment de la quantité de boucle dans le champ et n’affectent pas la force nette sur la boucle. (b) Si un courant de 5,00 A est utilisé, quelle est la force par tesla sur la boucle de 20,0 cm de large?

Diagramme montrant une boucle de fil rectangulaire dont une extrémité se trouve dans un champ magnétique présent dans une zone circulaire. Le champ B est orienté hors de la page. Le courant I circule dans le plan de la page, sur le côté gauche du circuit, vers la droite en bas du circuit et vers le haut sur le côté droit du circuit. La longueur du segment de fil qui court de gauche à droite en bas du circuit est de vingt centimètres de long.
Figure 8.

Solutions

Problèmes&Exercices

1: (a) ouest (gauche)

(b) dans la page

(c)nord (haut)

(d)pas de force

(e)est (droite)

(f)sud (bas)

3:(a) dans la page

(b) ouest (gauche)

(c) hors de la page

5:(a)2,50 N

(b) C’est environ une demi-livre de force par 100 m de fil, ce qui est beaucoup moins que le poids du fil lui-même. Par conséquent, cela ne suscite pas de préoccupations particulières.

7:1,80 T

9: (a) \boldsymbol {30^{\circ}}

(b) 4.80 N