Articles

főiskolai fizika

by admin

összefoglaló

  • írja le a mágneses erő hatását egy áramvezető vezetőre.
  • Számítsa ki az áramvezető mágneses erejét.

mivel a töltések általában nem tudnak elmenekülni egy vezetőtől, a vezetőben mozgó töltések mágneses ereje továbbításra kerül a vezetőnek.

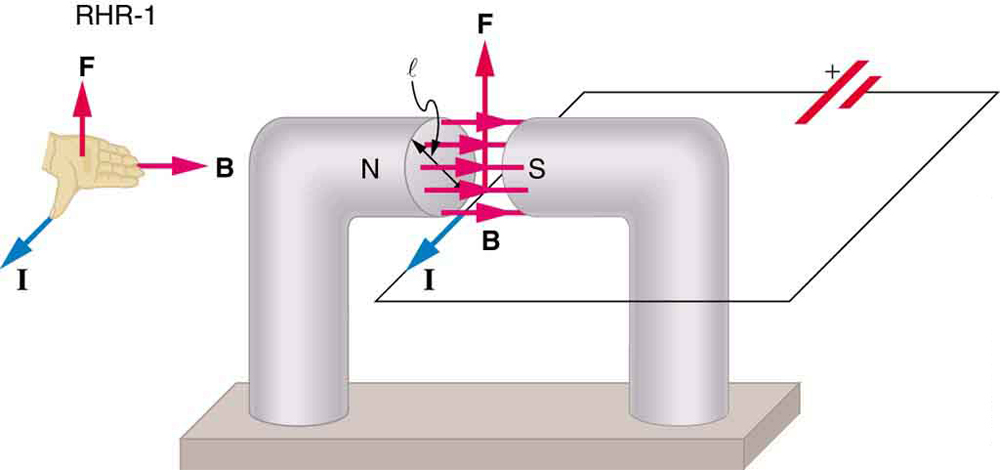
egy diagram, amely egy áramkört mutat, amelyen keresztül fut az I áram. A huzal egyik része áthalad egy átmérőjű mágnes északi és Déli pólusai között l. A B mágneses mező jobbra irányul, északról a mágnes déli pólusára, a huzalon keresztül. Az áram kifogy az oldalról. A huzalon lévő erő felfelé irányul. Az 1. jobb oldali szabály illusztrációja azt mutatja, hogy a hüvelykujj az oldalról az áram irányába mutat, az ujjak jobbra a B irányába mutatnak,az F vektor pedig felfelé és távol a tenyértől.
1.ábra. A mágneses mező erőt fejt ki az áramvezető huzalra az 1. jobb oldali szabály által megadott irányban (ugyanaz az irány, mint az egyes mozgó töltéseknél). Ez az erő könnyen elég nagy lehet a huzal mozgatásához, mivel a tipikus áramok nagyon nagy számú mozgó töltésből állnak.

a mágneses erő kifejezését az áramon az egyes töltések mágneses erőinek összegével tudjuk levezetni. (Az erők hozzá, mert ugyanabban az irányban.) A vdvd sodródási sebességnél mozgó egyedi töltés erejét a \boldsymbol{F = qv_dB \;\textbf{sin} \;\theta} adja. Figyelembe \ boldsymbol{b}, hogy egységes hosszú huzal \ boldsymbol{l} és nulla máshol, a teljes mágneses erő a vezeték akkor \ boldsymbol{F = (qv_dB \; \ textbf{sin} \; \ theta) (N)}, ahol \boldsymbol{n} a töltéshordozók száma a huzal hossza \boldsymbol{l}. Most, \ boldsymbol{n = nV}, ahol \ boldsymbol{n} az egységnyi térfogatra jutó töltéshordozók száma, \boldsymbol{v} pedig a mezőben lévő huzal térfogata. Megjegyezve, hogy \ boldsymbol{v=Al}, ahol \ boldsymbol{a} a huzal keresztmetszeti területe ,akkor a huzalon lévő erő \ boldsymbol{F=(qv_dB \; \ textbf{sin}\; \theta) (nAl)}.

\boldsymbol{F=(nqAv_d)lB \;\textbf{sin} \;\theta}.

mert \boldsymbol{nqav_d = i} (lásd a 20.1.fejezet jelenlegi),

\boldsymbol{F = IlB \;\textbf{sin} \;\theta}

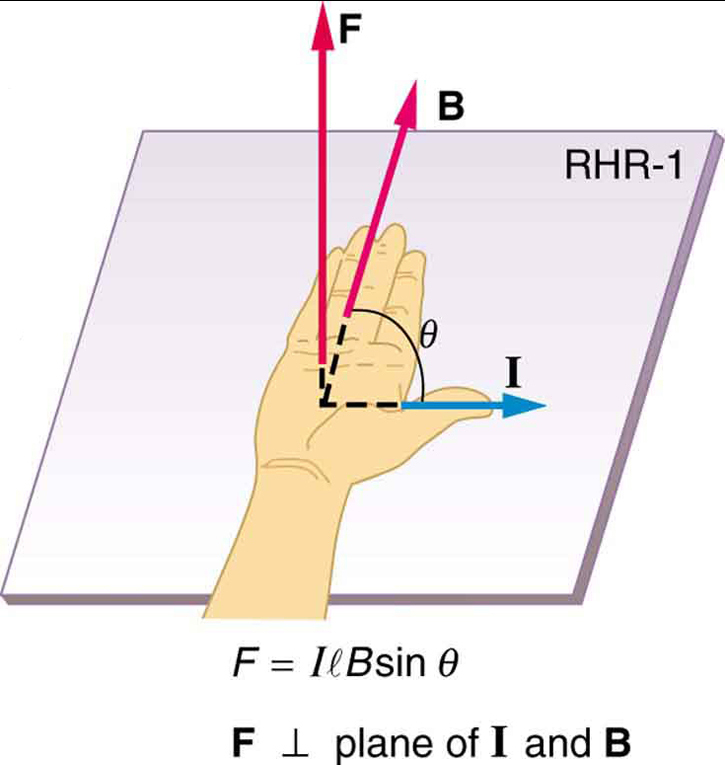
a mágneses erő egyenlete a \boldsymbol{l} huzal hosszán \boldsymbol{I} Egységes mágneses mezőben \boldsymbol{B}, a 2. ábrán látható módon. Ha ennek a kifejezésnek mindkét oldalát \boldsymbol{l} – vel osztjuk, azt találjuk, hogy a huzal egységhosszúságára jutó mágneses erő egy egységes mezőben \boldsymbol{\frac{F}{l} = IB \;\textbf{sin} \;\theta}. Ennek az erőnek az irányát az RHR-1 Adja meg, a hüvelykujjával a jelenlegi \boldsymbol{i} irányába. Ezután az ujjakkal a \ boldsymbol{B} irányában merőleges a tenyérre a \boldsymbol{F} irányába, mint a 2. ábrán.

a jobb oldali 1.szabály illusztrációja, amely a hüvelykujj jobbra mutat az I áram irányába, az ujjak az oldalra mutatnak B mágneses mezővel, és az erő felfelé, a tenyértől távol.
2.ábra. A mágneses mezőben lévő áramhordozó huzalon az erő F = IlB sin θ. Irányát az RHR-1 Adja.

mágneses erő kiszámítása áramvezető huzalon: Erős mágneses mező

Számítsa ki az erőt az 1. ábrán látható huzalon, megadva \ boldsymbol{B = 1,50\; \ textbf{t}}, \ boldsymbol{l = 5,00\; \ textbf{cm}}, és \ boldsymbol{I = 20,0\; \ textbf{a}}.

stratégia

az erő megtalálható a megadott információk segítségével \boldsymbol{F = IlB \;\textbf{sin} \;\theta} és megjegyezve, hogy a szög \boldsymbol{\theta} között \boldsymbol{i} és \boldsymbol{B} is \boldsymbol{90 ^{\circ}}}, úgy, hogy \boldsymbol{\textbf{sin}\; \Theta = 1}.

megoldás

a megadott értékek beírása \ boldsymbol{F = IlB \;\textbf{sin} \theta}

\boldsymbol{F = IlB \;\textbf{sin} \theta = (20.0 \;\textbf{a}) \; (0.0500 \;\textbf{m}) \; (1.50 \;\textbf{t})\; (1)}.

a tesla egységei \ boldsymbol{1\; \ textbf{t} = \ FRAC{\textbf{N}}} {\textbf{a} \cdot \; \textbf{m}}}}}; így

\ boldsymbol{F = 1,50\; \ textbf{n}}.

Vita

Ez a nagy mágneses mező jelentős erőt hoz létre egy kis huzalhosszon.

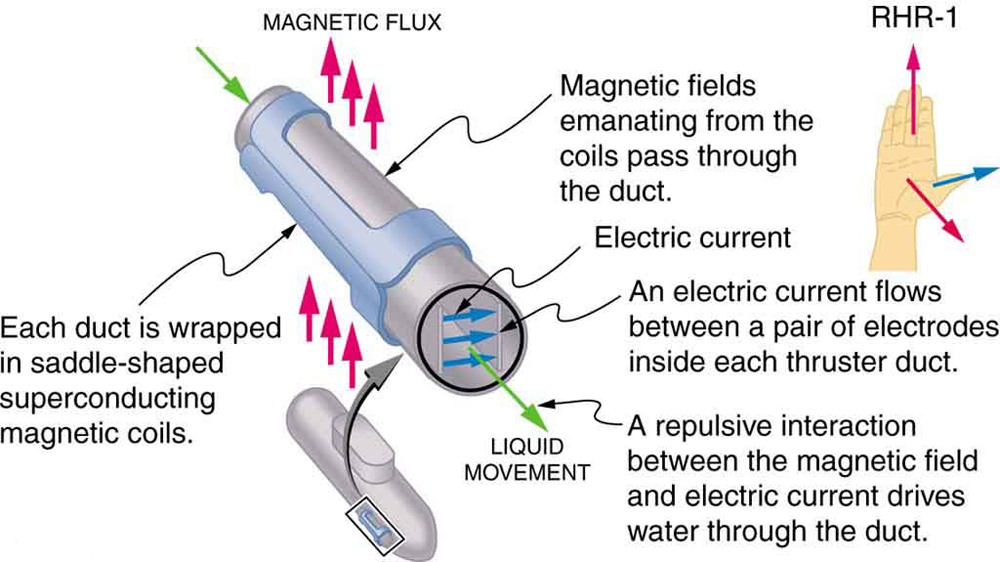
az áramvezető vezetékek mágneses erejét használják az elektromos energia átalakítására. (A motorok kiváló példa erre-huzalhurkokat alkalmaznak, amelyeket a következő szakaszban tekintünk meg.) A magnetohidrodinamika (MHD) az okos alkalmazásnak adott műszaki név, ahol a mágneses erő szivattyúzza a folyadékokat mechanikus alkatrészek mozgatása nélkül. (Lásd A 3. Ábrát.)

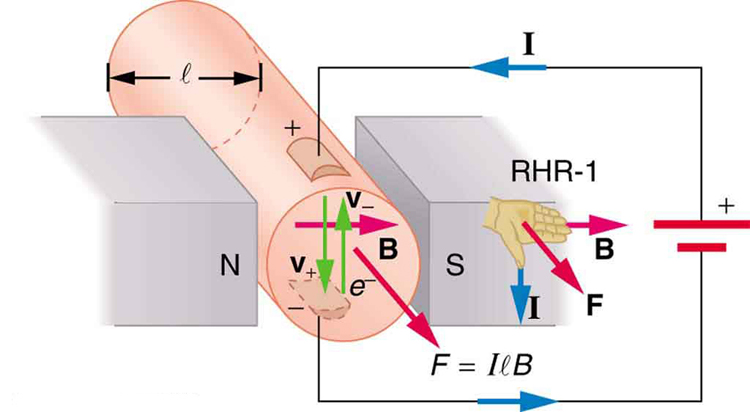
ábra, amelyen egy mágnes északi és Déli pólusai közé helyezett l átmérőjű folyadékhenger látható. Az Északi-sark balra van. A Déli-sark jobbra van. A henger az oldalon kívül helyezkedik el. A mágneses mező jobbra, északról a déli pólusra, valamint a folyadék hengerére irányul. Az áramvezető huzal a folyadékhengeren keresztül halad, az I áram lefelé orientált, merőleges a hengerre. A folyadékban lévő negatív töltések sebességvektorral felfelé mutatnak. A folyadékban lévő pozitív töltések sebességvektorral lefelé mutatnak. A folyadék ereje az oldalon kívül van. Az 1.jobb oldali szabály illusztrációja azt mutatja, hogy a hüvelykujj lefelé mutat az árammal, az ujjak jobbra mutatnak B-vel, az F-et pedig az oldalról, a tenyértől távol.
3. ábra. Magnetohidrodinamika. A folyadékon áthaladó áram mágneses ereje nem mechanikus szivattyúként használható.

erős mágneses mezőt alkalmaznak egy csövön, és egy áramot vezetnek át a folyadékon derékszögben a mezőre, ami a folyadéknak a cső tengelyével párhuzamos erejét eredményezi az ábrán látható módon. A mozgó alkatrészek hiánya vonzóvá teszi ezt egy forró, kémiailag aktív anyag, például az egyes atomreaktorokban alkalmazott folyékony nátrium mozgatásához. Kísérleti mesterséges szívek tesztelik ezt a technikát a vér szivattyúzására, talán megkerülve a mechanikus szivattyúk káros hatásait. (A sejtmembránokat azonban az MHD-ben szükséges nagy területek befolyásolják, késleltetve annak gyakorlati alkalmazását az emberekben.) A nukleáris tengeralattjárók MHD meghajtását javasolták, mivel ez lényegesen csendesebb lehet, mint a hagyományos propeller meghajtók. A nukleáris tengeralattjárók elrettentő értéke azon alapul, hogy képesek elrejteni és túlélni egy első vagy második nukleáris csapást. Ahogy lassan szétszereljük nukleáris fegyvereink arzenáljait, a tengeralattjáró ág lesz az utolsó, amelyet leszerelnek e képesség miatt (lásd a 4.ábrát.) A meglévő MHD meghajtók nehezek és nem hatékonyak—sok fejlesztési munkára van szükség.

diagram, amely nagyítást mutat egy nukleáris tengeralattjáró magnetohidrodinamikus meghajtórendszerére. A folyadék áthalad a tolócsatornán, amely az oldalról orientálódik. A mágneses mezők a tekercsekből származnak, és áthaladnak egy csatornán. A mágneses fluxus felfelé irányul, merőleges a csatornára. Minden csatorna nyereg alakú szupravezető tekercsekbe van csomagolva. Az elektromos áram jobbra, a folyadékon keresztül, a folyadék sebességére merőleges. Az elektromos áram egy pár elektróda között áramlik az egyes tolócsatornákban. A mágneses mező és az elektromos áram közötti visszataszító kölcsönhatás a vizet a csatornába vezeti. A jobb oldali szabály illusztrációja azt mutatja, hogy a hüvelykujj jobbra mutat az elektromos árammal. Az ujjak felfelé mutatnak a mágneses mezővel. A folyadék ereje az oldalról, a tenyértől távol helyezkedik el.
4.ábra. Egy nukleáris tengeralattjáró MHD meghajtórendszere lényegesen kevesebb turbulenciát okozhat, mint a propellerek, és lehetővé teszi, hogy csendesebben működjön. A silent drive tengeralattjáró fejlesztését dramatizálták a könyvben és a The Hunt for Red October című filmben.
  • az áramvezető vezetékek mágneses erejét
    \boldsymbol{F = IlB \;\textbf{sin} \;\theta},

    ahol \boldsymbol{i} az áram, \a boldsymbol{l} egy egyenes vezető hossza egy egységes mágneses mezőben \boldsymbol{b}, a \boldsymbol{\Theta} pedig a \boldsymbol{i} és \boldsymbol{B} közötti szög. Az erő az RHR-1-et követi a hüvelykujjával \boldsymbol{i} irányába.

fogalmi kérdések

1: Rajzoljon egy vázlatot az 1.ábrán látható helyzetről, amely bemutatja az áramot hordozó elektronok irányát, és RHR-1-et használjon a huzalon lévő erő irányának ellenőrzésére.

2: Ellenőrizze, hogy az MHD-meghajtóban lévő erő iránya, mint például a 3. ábrán, nem függ-e az áramot a folyadékban hordozó töltések jelétől.

3: Miért működne jobban egy magnetohidrodinamikus meghajtó az óceánvízben, mint az édesvízben? Továbbá, miért lenne kívánatos a szupravezető mágnesek?

4: Melyik nagyobb valószínűséggel zavarja az iránytű leolvasását, a hűtőszekrényben lévő váltakozó áramot vagy az egyenáramot az autó indításakor? Magyarázd meg.

problémák & gyakorlatok

1: Mi a mágneses erő iránya a jelenlegi hat esetben az 5. ábrán?

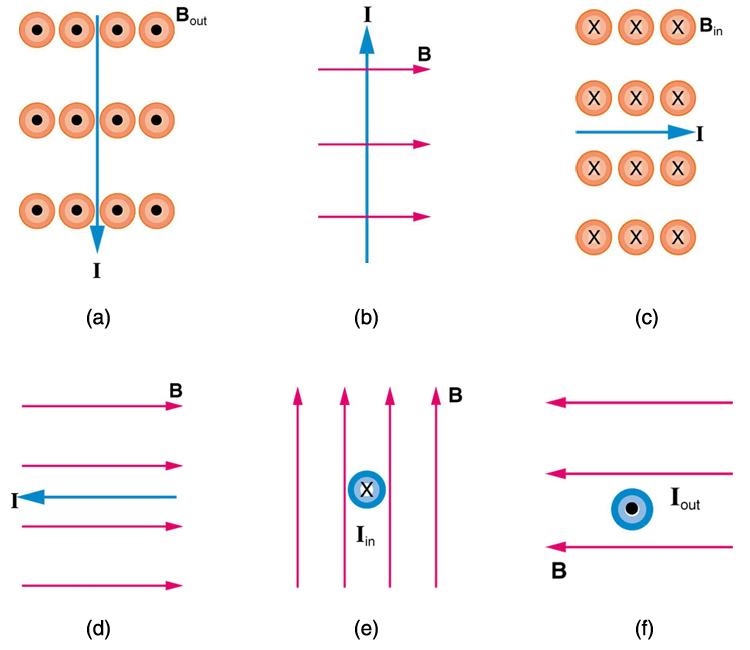
az A ábra A B mágneses mezőt mutatja ki az oldalról, és az aktuális I lefelé. A b ábra B-t mutat jobbra, én pedig felfelé. A c ábra B-t mutat az oldalra, én pedig jobbra. A d ábra B-t mutat jobbra, én pedig balra. Az e ábra B-t mutat felfelé, én pedig az oldalra. Az f ábra B-t mutat balra, én pedig ki az oldalról.
5.ábra.

2: mi annak az áramnak az iránya, amely a 6. ábrán látható három eset mindegyikében megtapasztalja a mágneses erőt, feltételezve, hogy az áram merőleges a \boldsymbol{B} – re?

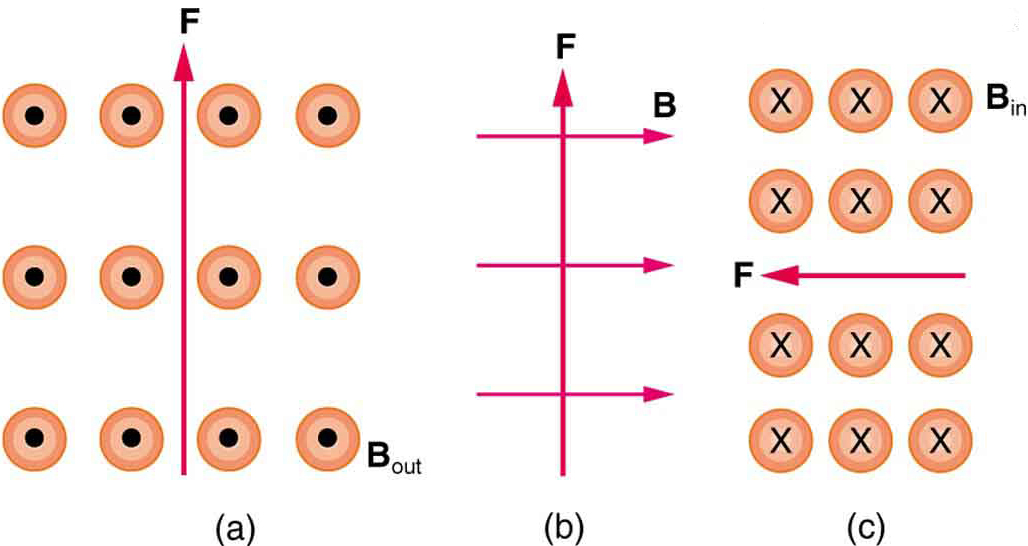
az A ábra A B mágneses mezőt mutatja ki az oldalról, és f-t felfelé kényszerít. A b ábra B-t mutat jobbra, F-et felfelé. A c ábra B-t mutat az oldalra, F-et pedig balra.
6. Ábra

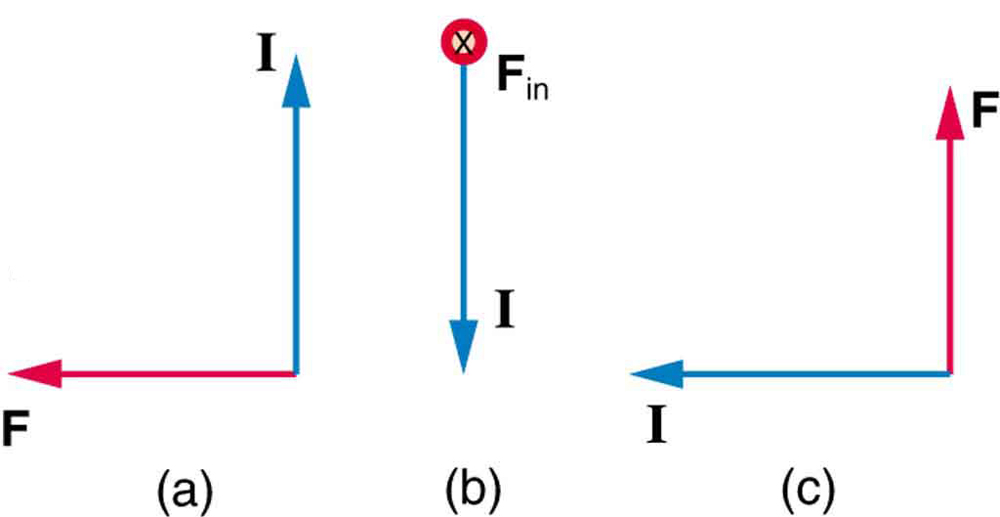
3: Mi az irányt a mágneses mező, amely termel a mágneses erő jelenik meg a áramlatok mind a három esetben a 7. Ábra, feltéve \boldsymbol{B} merőleges \boldsymbol{I}?

a ábra mutatja A felfelé mutató I vektort és a balra mutató F vektort. A b ábra az aktuális vektort mutatja lefelé, az F pedig az oldalra irányítva. A c ábra a balra mutató áramot és a felfelé mutató erőt mutatja.
7.ábra.

4: (a) mi az erő méterenként egy villám az egyenlítőn, amely 20 000 A – t hordoz merőlegesen a Föld \boldsymbol{3.00 \times 10^{-5} – \textbf{t}} mezőre? b) mi az erő iránya, ha az áram egyenesen felfelé halad, és a Föld mező iránya észak felé, a talajjal párhuzamosan történik?

5: (a) egy egyenáramú tápvezeték egy könnyű vasúti rendszer hordoz 1000 a szögben \boldsymbol{30.0 ^{\circ}} a Föld \boldsymbol{5.00 \times 10^{-5}-\textbf{t}} mező. Mi az erő a vonal 100 m-es szakaszán? b) megvitassák az ezzel kapcsolatos gyakorlati aggályokat, ha vannak ilyenek.

6: Milyen erő van gyakorolt a víz egy MHD meghajtó kihasználva a 25.0 cm-es átmérőjű csövet, ha 100-áram halad át a csövet, hogy merőleges egy 2.00-T mágneses mező? (Ennek az erőnek a viszonylag kis mérete azt jelzi, hogy nagyon nagy áramokra és mágneses mezőkre van szükség a praktikus MHD meghajtók készítéséhez.)

7: drót kezében egy 30.0-Egy aktuális áthalad a lengyelek egy erős mágnes, ami merőleges a mezőbe, majd a tapasztalatok egy 2.16-N erő a 4.00 cm vezetéket, a mező. Mi az átlagos térerősség?

8: (a) Egy 0.750 m hosszú szakasz a kábel szállító aktuális, hogy egy autó indítómotor tesz egy szög \boldsymbol{60^{\circ}} a Föld \boldsymbol{5.50 \alkalommal 10^{-5} \;\textbf{T}} területen. Mi az áram, ha a huzal \boldsymbol{7.00 \times 10^{-3} \;\textbf{N}} erőt tapasztal? b) ha a huzalt egy erős patkómágnes pólusai között futtatja, 5, 00 cm-t 1, 75 T-es mezőnek vetve alá, milyen erő van a huzal ezen szegmensére?

9: A) mi a szög egy 8,00-a áramot hordozó huzal és az 1,20-T mező között, ha a huzal 50,0 cm-e 2,40 N mágneses erőt tapasztal? (b) Mi az erő a huzalon, ha el van forgatva, hogy \boldsymbol{90^{\circ} szöget készítsen a mezővel?

10: a 8. ábrán látható mágneses mezőben a huzal téglalap alakú hurokján lévő erő felhasználható a térerősség mérésére. A mező egyenletes, a hurok síkja merőleges a mezőre. a) mi a mágneses erő iránya a hurokon? Igazolja azt az állítást, hogy a hurok oldalán lévő erők egyenlőek és ellentétesek, függetlenül attól, hogy a hurok mekkora része van a mezőben, és nem befolyásolják a hurok nettó erejét. b) ha 5.00 A áramot használunk, mekkora erő van teslánként a 20.0 cm széles hurokban?

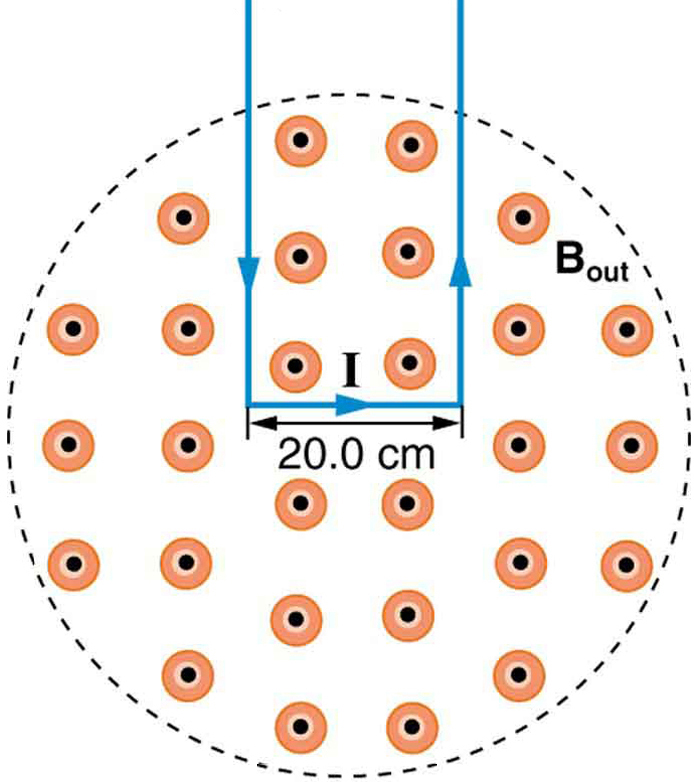
Diagram, amely egy téglalap alakú huzalhurkot mutat, amelynek egyik vége egy kör alakú területen lévő mágneses mezőn belül van. A b mező az oldalon kívül helyezkedik el. Az áram az oldal síkjában fut, az áramkör bal oldalán, az áramkör alján jobbra, az áramkör jobb oldalán felfelé. Az áramkör alján balról jobbra futó huzalszakasz hossza húsz centiméter hosszú.
8.ábra.

Megoldás

a Problémák & Gyakorlatok

1: (a) nyugati (bal)

(b) a oldal

(c) északi (up)

(d) nincs erő

(e) keleti (jobb)

(f) dél (le)

3: (a) az oldalon

(b) nyugati (bal)

(c) az oldal

5: (a) 2.50 N

(b) Ez egy fél kiló erő / 100 m drót, ami sokkal kevesebb, mint a tömeg, a drót is. Ezért nem okoz különösebb aggodalmat.

7: 1,80 T

9: (a) \boldsymbol{30^{\circ}}

(b) 4.80 N