Articles

College Physics

by admin Giugno 24, 2021

Sommario

Descrivi gli effetti di una forza magnetica su un conduttore che trasporta corrente.
Calcola la forza magnetica su un conduttore che trasporta corrente.

Poiché le cariche normalmente non possono sfuggire a un conduttore, la forza magnetica sulle cariche che si muovono in un conduttore viene trasmessa al conduttore stesso.

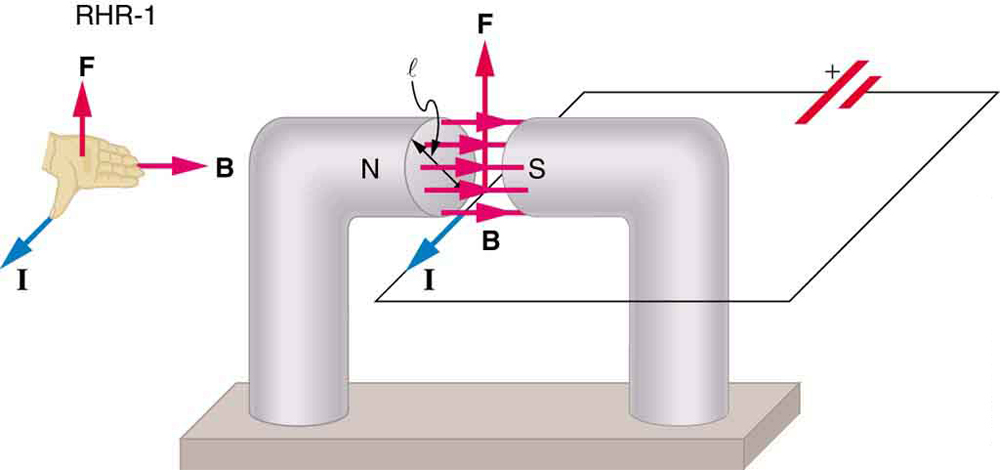
Un diagramma che mostra un circuito con corrente I che lo attraversa. Una sezione del filo passa tra i poli nord e sud di un magnete con un diametro l. Il campo magnetico B è orientato verso destra, dal polo nord al polo sud del magnete, attraverso il filo. La corrente esaurisce la pagina. La forza sul filo è diretta verso l'alto. Un'illustrazione della regola della mano destra 1 mostra il pollice che punta fuori dalla pagina nella direzione della corrente, le dita che puntano a destra nella direzione di B e il vettore F che punta verso l'alto e lontano dal palmo. — Figura 1. Il campo magnetico esercita una forza su un filo che trasporta corrente in una direzione data dalla regola della mano destra 1 (la stessa direzione di quella delle singole cariche in movimento). Questa forza può essere facilmente abbastanza grande da spostare il filo, poiché le correnti tipiche consistono in un numero molto elevato di cariche mobili.

Possiamo ricavare un’espressione per la forza magnetica su una corrente prendendo una somma delle forze magnetiche su singole cariche. (Le forze aggiungono perché sono nella stessa direzione.) La forza su una singola carica che si muove alla velocità di deriva vdvd è data da \ boldsymbol{F = qv_dB \;\textbf{sin} \;\theta}. Prendendo \boldsymbol{B} per essere uniforme su una lunghezza di filo \boldsymbol{l} e zero altrove, il totale della forza magnetica su un filo è poi \boldsymbol{F = (qv_dB \;\textbf{peccato} \;\theta)(N)}, dove \boldsymbol{N} è il numero di portatori di carica nella sezione di filo di lunghezza \boldsymbol{l}. Ora, \ boldsymbol{N=nV}, dove \ boldsymbol{n} è il numero di portatori di carica per unità di volume e \boldsymbol{V} è il volume del filo nel campo. Notando che \ boldsymbol {V = Al}, dove \ boldsymbol{A} è l’area della sezione trasversale del filo, quindi la forza sul filo è \ boldsymbol {F = (qv_dB \;\textbf{sin} \;\theta) (nAl)}. La raccolta di termini,

\boldsymbol{F=(nqAv_d)lB \;\textbf{sin} \;\theta}.

Perché \boldsymbol{nqAv_d = I} (vedere il Capitolo 20.1 Corrente),

\boldsymbol{F = IlB \;\textbf{peccato} \;\theta}

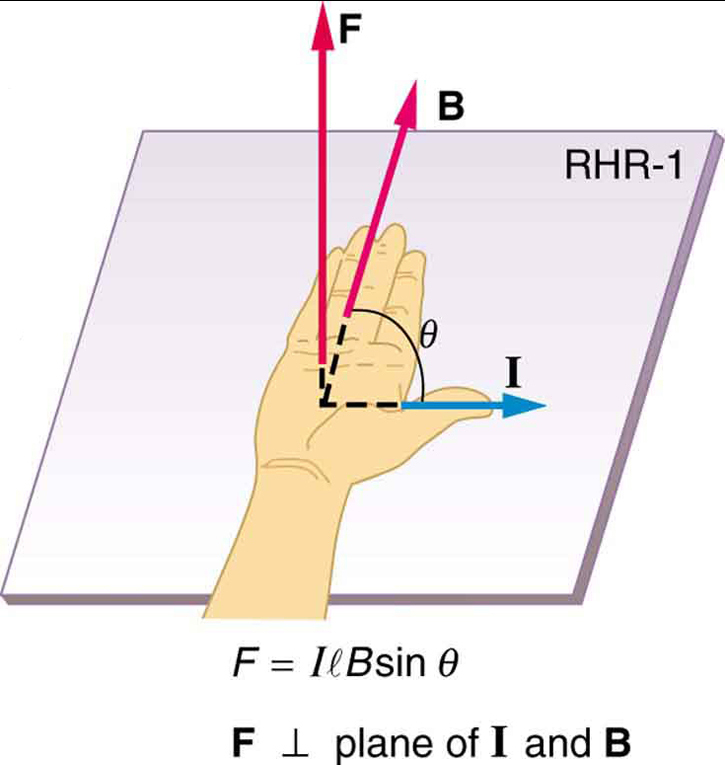
è l’equazione della forza magnetica su una lunghezza \boldsymbol{l} di filo trasporta una corrente \boldsymbol{I} in un campo magnetico uniforme \boldsymbol{B} come mostrato in Figura 2. Se dividiamo entrambi i lati di questa espressione per \ boldsymbol {l}, troviamo che la forza magnetica per unità di lunghezza del filo in un campo uniforme è \ boldsymbol {\frac {F} {l} = IB \;\textbf {sin}\; \theta}. La direzione di questa forza è data da RHR-1, con il pollice nella direzione della corrente \boldsymbol{I}. Quindi, con le dita nella direzione di \ boldsymbol {B}, una perpendicolare al palmo punta nella direzione di \ boldsymbol {F}, come in Figura 2.

Illustrazione della regola della mano destra 1 che mostra il pollice che punta a destra nella direzione della corrente I, le dita che puntano nella pagina con campo magnetico B e la forza diretta verso l'alto, lontano dal palmo. — Figura 2. La forza su un filo che trasporta corrente in un campo magnetico è F = ILB sin θ. La sua direzione è data da RHR-1.

Calcolo della forza magnetica su un filo che trasporta corrente: Un forte campo magnetico

Calcola la forza sul filo mostrato in Figura 1, dato \boldsymbol{B = 1.50 \;\textbf{T}}, \boldsymbol{l = 5.00 \;\textbf{cm}}, e \boldsymbol{I = 20.0 \;\textbf{A}}.

la Strategia

La forza può essere trovato con le informazioni utilizzando \boldsymbol{F = IlB \;\textbf{peccato} \;\theta} e notando che l’angolo \boldsymbol{\theta} tra \boldsymbol{I} e \boldsymbol{B} è \boldsymbol{90 ^{\circ}}, in modo che \boldsymbol{\textbf{peccato} \;\theta = 1}.

Soluzione

Inserire i valori dati in \ boldsymbol{F = IlB \;il nostro sito utilizza cookie tecnici e di terze parti per migliorare la tua esperienza di navigazione e per migliorare la tua esperienza di navigazione.

Le unità per tesla sono \boldsymbol{1 \;\textbf{T} = \frac{\textbf{N}}{\textbf{A} \cdot \; \textbf{m}}}; quindi,

\boldsymbol{F = 1.50 \;\textbf{N}}.

Discussione

Questo grande campo magnetico crea una forza significativa su una piccola lunghezza di filo.

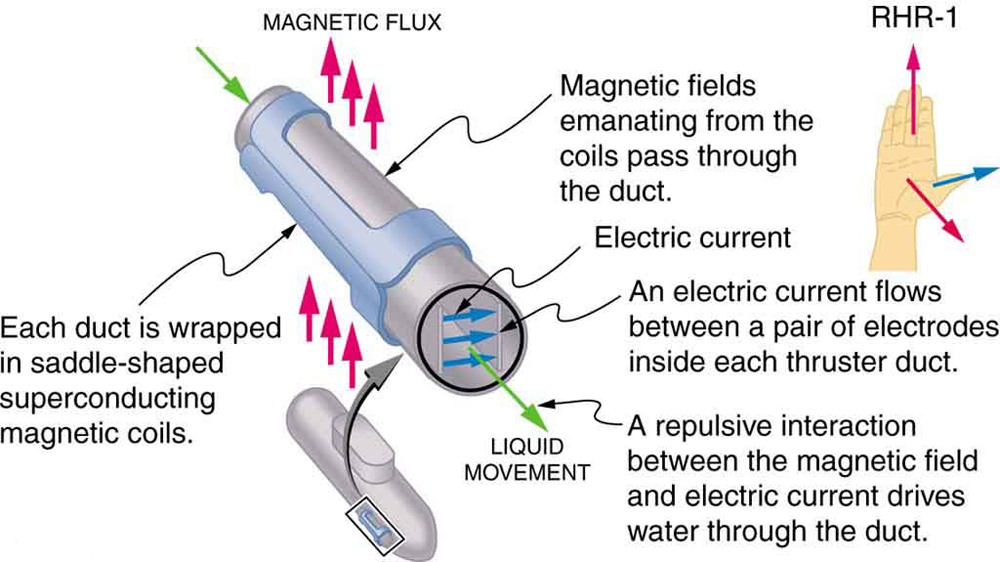
La forza magnetica sui conduttori che trasportano corrente viene utilizzata per convertire l’energia elettrica in lavoro. (I motori sono un primo esempio: impiegano anelli di filo e sono considerati nella sezione successiva.) Magnetoidrodinamica (MHD) è il nome tecnico dato a un’applicazione intelligente in cui la forza magnetica pompa fluidi senza muovere parti meccaniche. (Vedi Figura 3.)

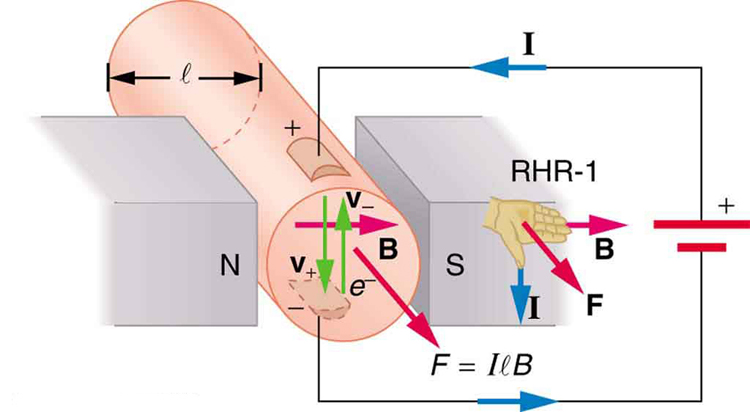
Diagramma che mostra un cilindro di fluido di diametro l posto tra i poli nord e sud di un magnete. Il polo nord è a sinistra. Il polo sud è a destra. Il cilindro è orientato fuori dalla pagina. Il campo magnetico è orientato verso destra, dal polo nord al polo sud e attraverso il cilindro del fluido. Un filo che trasporta corrente attraversa il cilindro del fluido con corrente I orientata verso il basso, perpendicolare al cilindro. Le cariche negative all'interno del fluido hanno un vettore di velocità rivolto verso l'alto. Le cariche positive all'interno del fluido hanno un vettore di velocità rivolto verso il basso. La forza sul fluido è fuori dalla pagina. Un'illustrazione della regola della mano destra 1 mostra il pollice rivolto verso il basso con la corrente, le dita rivolte a destra con B e la forza F orientata fuori dalla pagina, lontano dal palmo. — Figura 3. Magnetoidrodinamica. La forza magnetica sulla corrente passata attraverso questo fluido può essere utilizzata come pompa non meccanica.

Un forte campo magnetico viene applicato attraverso un tubo e una corrente viene fatta passare attraverso il fluido ad angolo retto rispetto al campo, con conseguente forza sul fluido parallelo all’asse del tubo come mostrato. L’assenza di parti mobili rende questo attraente per lo spostamento di una sostanza calda, chimicamente attiva, come il sodio liquido impiegato in alcuni reattori nucleari. I cuori artificiali sperimentali stanno testando con questa tecnica per pompare il sangue, forse aggirando gli effetti negativi delle pompe meccaniche. (Membrane cellulari, tuttavia, sono influenzati dai grandi campi necessari in MHD, ritardando la sua applicazione pratica negli esseri umani.) La propulsione MHD per sottomarini nucleari è stata proposta, perché potrebbe essere notevolmente più silenziosa rispetto ai propulsori convenzionali. Il valore deterrente dei sottomarini nucleari si basa sulla loro capacità di nascondere e sopravvivere a un primo o secondo attacco nucleare. Mentre smontiamo lentamente i nostri arsenali di armi nucleari, il ramo sottomarino sarà l’ultimo ad essere disattivato a causa di questa capacità (vedi Figura 4.) Le unità MHD esistenti sono pesanti e inefficienti—è necessario molto lavoro di sviluppo.

Diagramma che mostra un ingrandimento di un sistema di propulsione magnetoidrodinamica su un sottomarino nucleare. Il liquido si muove attraverso il condotto del propulsore, che è orientato fuori dalla pagina. I campi magnetici emanano dalle bobine e passano attraverso un condotto. Il flusso magnetico è orientato verso l'alto, perpendicolare al condotto. Ogni condotto è avvolto in bobine superconduttrici a forma di sella. Una corrente elettrica corre a destra, attraverso il liquido e perpendicolare alla velocità del liquido. La corrente elettrica scorre tra una coppia di elettrodi all'interno di ciascun condotto del propulsore. Un'interazione repulsiva tra il campo magnetico e la corrente elettrica spinge l'acqua attraverso il condotto. Un'illustrazione della regola della mano destra mostra il pollice che punta a destra con la corrente elettrica. Le dita puntano verso l'alto con il campo magnetico. La forza sul liquido è orientata fuori dalla pagina, lontano dal palmo. — Figura 4. Un sistema di propulsione MHD in un sottomarino nucleare potrebbe produrre significativamente meno turbolenza rispetto alle eliche e consentirgli di funzionare in modo più silenzioso. Lo sviluppo di un sottomarino silent drive è stato drammatizzato nel libro e nel film The Hunt for Red October.

La forza magnetica su conduttori percorsi da corrente è data da
\boldsymbol{F = IlB \;\textbf{peccato} \;\theta},

dove \boldsymbol{I} è l’attuale, \boldsymbol{l} è la lunghezza di un diritto del conduttore in un campo magnetico uniforme \boldsymbol{B} e \boldsymbol{\theta} è l’angolo tra \boldsymbol{I} e \boldsymbol{B}. La forza segue RHR-1 con il pollice nella direzione di \ boldsymbol{I}.

Domande concettuali

1: Disegna uno schizzo della situazione in Figura 1 che mostra la direzione degli elettroni che trasportano la corrente e usa RHR-1 per verificare la direzione della forza sul filo.

2: Verificare che la direzione della forza in un’unità MHD, come quella in Figura 3, non dipenda dal segno delle cariche che trasportano la corrente attraverso il fluido.

3: Perché un azionamento magnetoidrodinamico dovrebbe funzionare meglio nell’acqua dell’oceano che nell’acqua dolce? Inoltre, perché i magneti superconduttori sarebbero desiderabili?

4: Quale è più probabile che interferisca con le letture della bussola, la corrente alternata nel frigorifero o la corrente continua quando si avvia l’auto? Spiegare.

Problemi& Esercizi

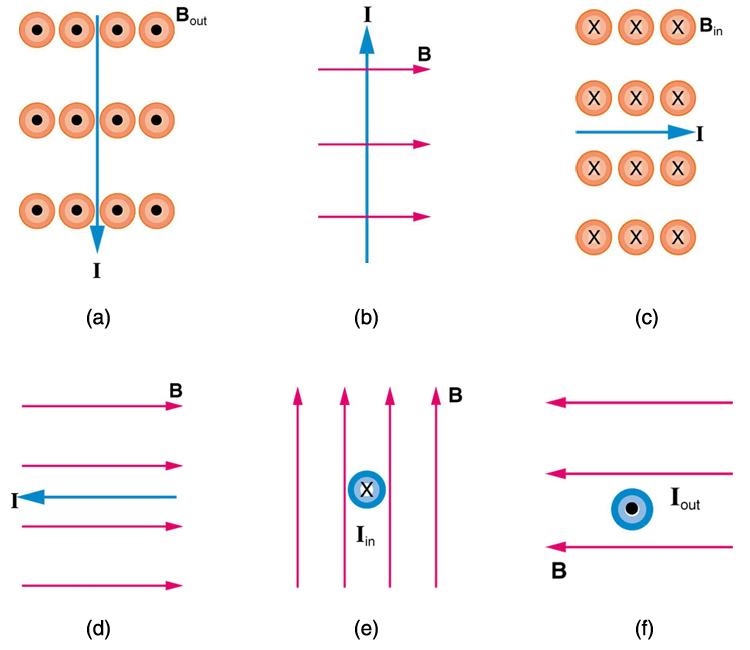
1: Qual è la direzione della forza magnetica sulla corrente in ciascuno dei sei casi in Figura 5?

La figura a mostra il campo magnetico B fuori dalla pagina e la corrente I verso il basso. La figura b mostra B verso destra e I verso l'alto. La figura c mostra B nella pagina e I verso destra. La figura d mostra B verso destra e I verso sinistra. La figura e mostra B verso l'alto e I nella pagina. La figura f mostra B verso sinistra e I fuori dalla pagina. — Figura 5.

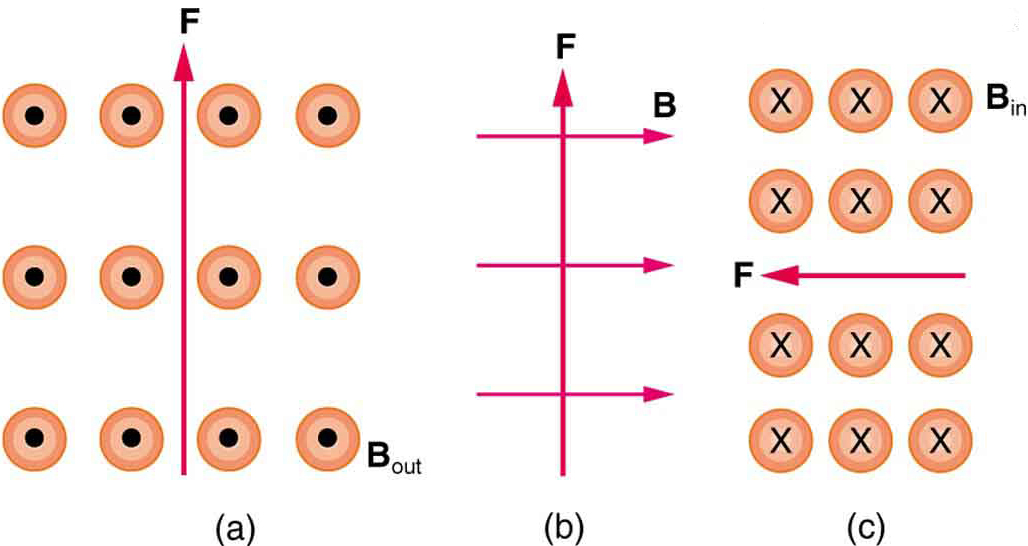
2: Qual è la direzione di una corrente che sperimenta la forza magnetica mostrata in ciascuno dei tre casi in Figura 6, supponendo che la corrente funzioni perpendicolarmente a \boldsymbol{B}?

La figura a mostra il campo magnetico B fuori dalla pagina e forza F verso l'alto. La figura b mostra B verso destra e F verso l'alto. La figura c mostra B nella pagina e F verso sinistra. — Figura 6

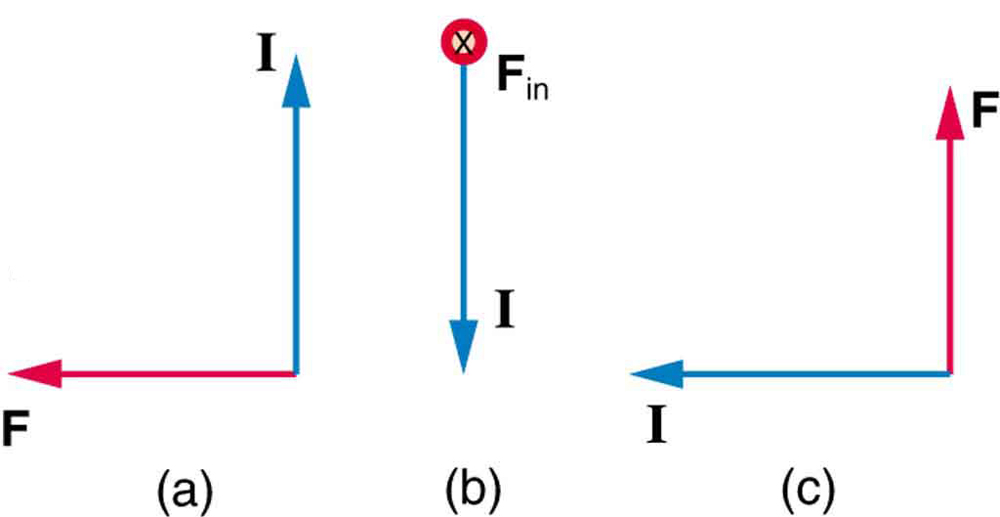
3: Qual è la direzione del campo magnetico che produce la forza magnetica mostrato le correnti in ciascuno dei tre casi in Figura 7, assumendo \boldsymbol{B} è perpendicolare a \boldsymbol{I}?

La figura a mostra il vettore corrente I rivolto verso l'alto e il vettore forza F rivolto verso sinistra. La figura b mostra il vettore corrente rivolto verso il basso e F diretto nella pagina. La figura c mostra la corrente che punta a sinistra e la forza che punta verso l'alto. — Figura 7.

4: (a) Qual è la forza per metro su un fulmine all’equatore che trasporta 20.000 A perpendicolare al campo \boldsymbol{3.00 \times 10^{-5} – \textbf{T}} della Terra? (b) Qual è la direzione della forza se la corrente è diretta verso l’alto e la direzione del campo terrestre è verso nord, parallela al suolo?

5: (a) Una linea di alimentazione CC per un sistema di binari leggeri trasporta 1000 A con un angolo di \boldsymbol{30.0 ^{\circ}} rispetto al campo \boldsymbol{5.00 \times 10^{-5}-\textbf{T}} della Terra. Qual è la forza su una sezione di 100 m di questa linea? (b) Discutere le preoccupazioni pratiche che questo presenta, se del caso.

6: Quale forza viene esercitata sull’acqua in un azionamento MHD che utilizza un tubo di 25,0 cm di diametro, se la corrente di 100 A viene fatta passare attraverso il tubo perpendicolare a un campo magnetico di 2,00 T? (La dimensione relativamente piccola di questa forza indica la necessità di correnti e campi magnetici molto grandi per realizzare unità MHD pratiche.)

7: Un filo che trasporta una corrente 30.0-A passa tra i poli di un magnete forte che è perpendicolare al suo campo e sperimenta una forza 2.16-N sui 4.00 cm di filo nel campo. Qual è l’intensità media del campo?

8: (a) Un tratto di cavo lungo 0,750 m che trasporta corrente a un motorino di avviamento per auto crea un angolo di \boldsymbol{60^{\circ}} con il campo \boldsymbol{5,50 \volte 10^{-5} \;\textbf{T}} della Terra. Qual è la corrente quando il filo subisce una forza di \ boldsymbol{7.00 \ volte 10^{-3}\; \ textbf{N}}? (b) Se si esegue il filo tra i poli di un forte magnete a ferro di cavallo, sottoponendo 5,00 cm di esso a un campo di 1,75-T, quale forza viene esercitata su questo segmento di filo?

9: (a) Qual è l’angolo tra un filo che trasporta una corrente 8.00-A e il campo 1.20-T in cui si trova se 50.0 cm del filo subisce una forza magnetica di 2.40 N? (b) Qual è la forza sul filo se viene ruotato per creare un angolo di \boldsymbol{90^{\circ}} con il campo?

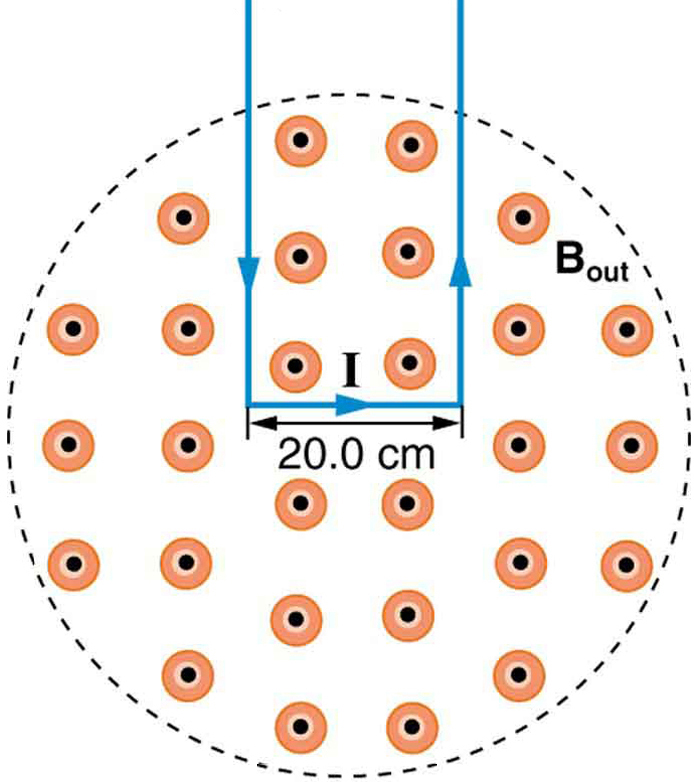
10: La forza sull’anello rettangolare del filo nel campo magnetico in Figura 8 può essere utilizzata per misurare l’intensità del campo. Il campo è uniforme e il piano del ciclo è perpendicolare al campo. (a) Qual è la direzione della forza magnetica sul ciclo? Giustificare l’affermazione che le forze sui lati del ciclo sono uguali e opposte, indipendentemente da quanto del ciclo è nel campo e non influenzano la forza netta sul ciclo. (b) Se viene utilizzata una corrente di 5,00 A, qual è la forza per tesla sul loop largo 20,0 cm?

Diagramma che mostra un anello rettangolare di filo, la cui estremità si trova all'interno di un campo magnetico presente all'interno di un'area circolare. Il campo B è orientato fuori dalla pagina. La corrente I corre nel piano della pagina, lungo il lato sinistro del circuito, verso destra nella parte inferiore del circuito e verso l'alto sul lato destro del circuito. La lunghezza del segmento di filo che corre da sinistra a destra nella parte inferiore del circuito è lunga venti centimetri. — Figura 8.

Soluzioni

Problemi & Esercizi

1: (a) a ovest (a sinistra)

(b) nella pagina

(d) nessuna forza

(e) a est (a destra)

(f) a sud (verso il basso)

3: (a) nella pagina

(b) a ovest (a sinistra)

5: (a) 2.50 N

(b) è di circa mezzo chilo di forza per 100 m di filo, che è molto meno il peso del filo stesso. Pertanto, non causa particolari preoccupazioni.

7: 1,80 T

9: (a) \boldsymbol{30^{\circ}}

(b) 4.80 N

Micro Blogs