Articles

College fysik

by admin

sammanfattning

  • beskriv effekterna av en magnetisk kraft på en strömbärande ledare.
  • beräkna den magnetiska kraften på en strömbärande ledare.

eftersom laddningar vanligtvis inte kan undkomma en ledare överförs den magnetiska kraften på laddningar som rör sig i en ledare till ledaren själv.

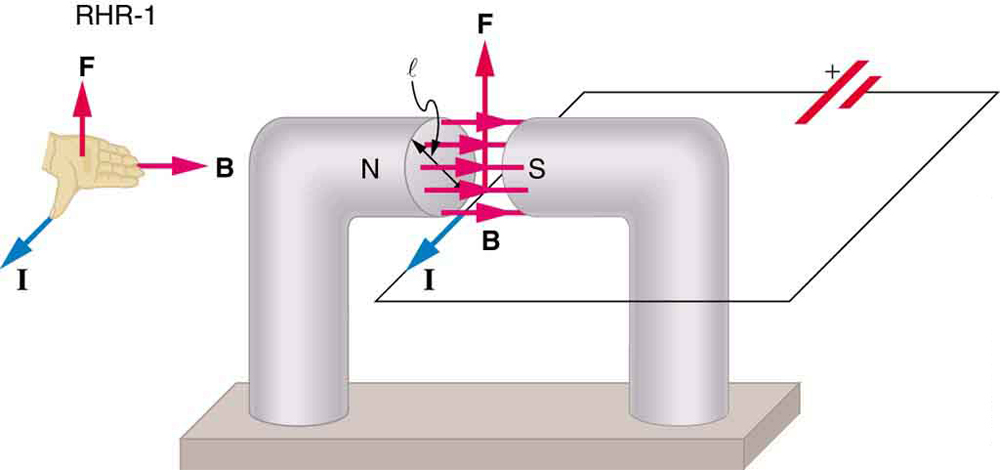
ett diagram som visar en krets med ström kör genom den. En sektion av tråden passerar mellan norra och södra polerna på en magnet med en diameter l. magnetfältet B är orienterat mot höger, från norr till magnetens sydpol, över tråden. Den nuvarande tar slut på sidan. Kraften på tråden riktas uppåt. En illustration av höger regel 1 visar tummen som pekar ut på sidan i strömriktningen, fingrarna pekar åt höger i riktning mot B och f-vektorn pekar uppåt och bort från handflatan.
Figur 1. Magnetfältet utövar en kraft på en strömbärande tråd i en riktning som ges av höger regel 1 (samma riktning som den på de enskilda rörliga laddningarna). Denna kraft kan lätt vara tillräckligt stor för att flytta tråden, eftersom typiska strömmar består av mycket stort antal rörliga laddningar.

Vi kan härleda ett uttryck för den magnetiska kraften på en ström genom att ta en summa av de magnetiska krafterna på individuella laddningar. (Krafterna lägger till eftersom de är i samma riktning.) Kraften på en individuell laddning som rör sig vid drivhastigheten vdvd ges av \ boldsymbol{F = qv_dB \; \ textbf{sin} \; \ theta}. Med \ boldsymbol{B} för att vara enhetlig över en längd av tråd \boldsymbol{l} och noll någon annanstans är den totala magnetiska kraften på tråden då \boldsymbol{F = (qv_dB \;\textbf{sin} \;\theta) (N)}, där \boldsymbol{n} är antalet laddningsbärare i avsnittet av tråd av längd \boldsymbol{l}. Nu, \ boldsymbol{N=nV}, där \boldsymbol{n} är antalet laddningsbärare per volymenhet och \boldsymbol{V} är volymen av tråd i fältet. Notera att \ boldsymbol{V=Al}, där \boldsymbol{a} är trådens tvärsnittsarea, då är kraften på tråden \boldsymbol{F=(qv_dB \;\textbf{sin} \;\theta) (nAl)}. Samla termer,

\boldsymbol{F=(nqAv_d)lB \;\textbf{sin} \;\theta}.

eftersom \boldsymbol{nqAv_d = i} (se kapitel 20.1 ström),

\boldsymbol{F = IlB \;\textbf{sin} \;\theta}

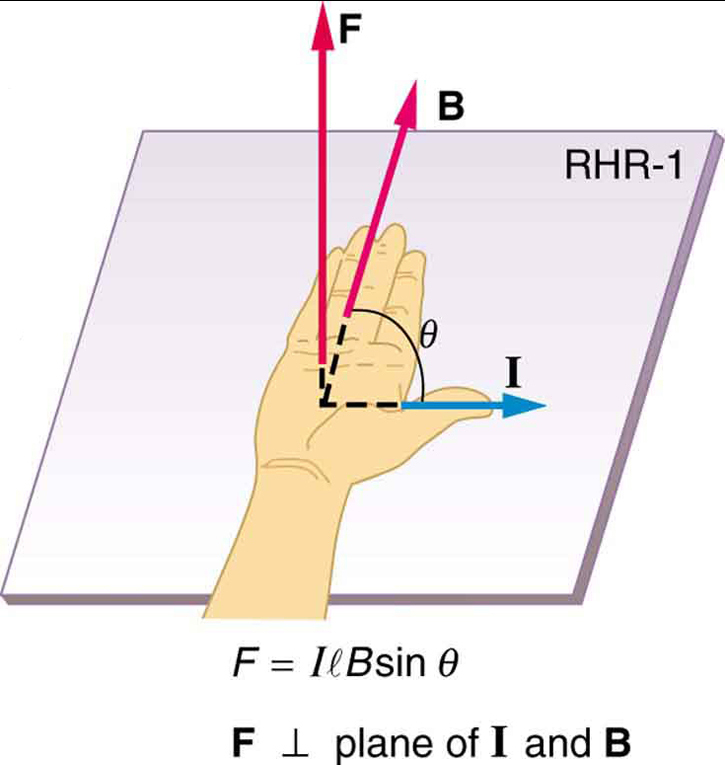
är ekvationen för magnetisk kraft på en längd \boldsymbol{l} av tråd som bär en ström \boldsymbol{i} i en enhetlig magnetisk kraft fält \fetsymbol{B}, som visas i Figur 2. Om vi delar båda sidor av detta uttryck med \boldsymbol{l}, finner vi att den magnetiska kraften per enhetslängd av tråd i ett enhetligt fält är \boldsymbol{\frac{F}{l} = IB \;\textbf{sin} \;\theta}. Riktningen för denna kraft ges av RHR-1, med tummen i riktning mot strömmen \boldsymbol{i}. Sedan, med fingrarna i riktning mot \boldsymbol{B}, pekar a vinkelrätt mot handflatan i riktning mot \boldsymbol{F}, som i Figur 2.

Illustration av höger handregel 1 som visar tummen som pekar åt höger i strömriktningen i, fingrarna pekar in på sidan med magnetfält B och kraften riktad uppåt, bort från handflatan.
Figur 2. Kraften på en strömbärande tråd i ett magnetfält är F = IlB sin ASIC. Dess riktning ges av RHR-1.

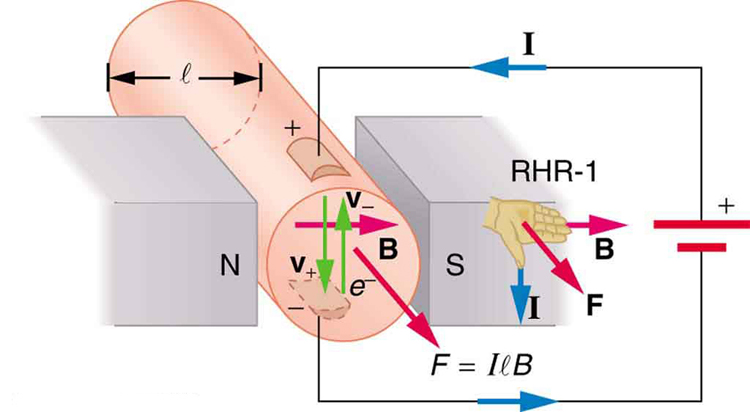
beräkning av magnetisk kraft på en strömbärande tråd: Ett starkt magnetfält

beräkna kraften på tråden som visas i Figur 1, Givet \boldsymbol{B = 1,50\; \textbf{t}}, \boldsymbol{l = 5,00\; \textbf{cm}} och \boldsymbol{i = 20,0\; \ textbf{a}}.

strategi

kraften kan hittas med den givna informationen genom att använda \boldsymbol{F = IlB\; \textbf{sin} \;\theta} och notera att vinkeln \boldsymbol {\theta} mellan \boldsymbol{i} och \boldsymbol{B} är \boldsymbol{90 ^{\circ}}, så att \boldsymbol{\textbf{sin} \;\theta = 1}.

lösning

Ange de angivna värdena i \ boldsymbol{F = IlB \;\textbf{sin}\theta} ger

\boldsymbol{F = IlB\; \textbf{sin} \theta = (20.0\; \ textbf{a})\; (0.0500\; \textbf{m}) \; (1.50\; \ textbf{t})\; (1)}.

enheterna för tesla är \ boldsymbol{1 \; \ textbf{t} = \frac{\textbf{N}}{\textbf{A} \cdot \; \textbf{m}}}; således

\boldsymbol{F = 1.50\; \textbf{N}}.

diskussion

detta stora magnetfält skapar en signifikant kraft på en liten trådlängd.

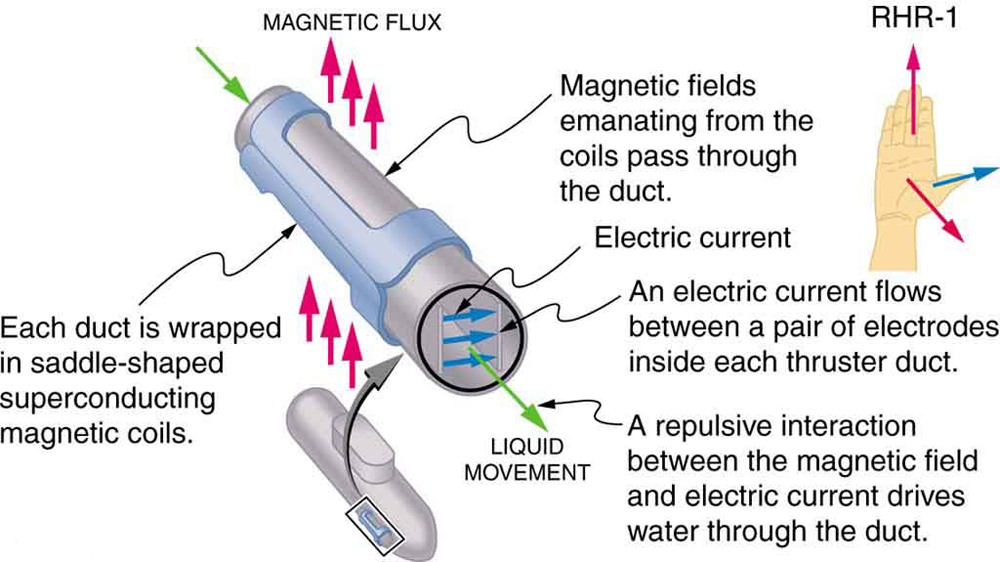
magnetisk kraft på strömbärande ledare används för att omvandla elektrisk energi till arbete. (Motorer är ett utmärkt exempel – de använder slingor av tråd och beaktas i nästa avsnitt.) Magnetohydrodynamics (MHD) är det tekniska namnet som ges till en smart applikation där magnetisk kraft pumpar vätskor utan att flytta mekaniska delar. (Se Figur 3.)

Diagram som visar en cylinder av vätska med diameter l placerad mellan norra och södra polerna på en magnet. Nordpolen är till vänster. Sydpolen är till höger. Cylindern är orienterad ur sidan. Magnetfältet är orienterat mot höger, från norr till Sydpolen och över vätskefiltern. En strömbärande tråd löper genom vätskecylindern med ström i orienterad nedåt, vinkelrätt mot cylindern. Negativa laddningar i vätskan har en hastighetsvektor som pekar uppåt. Positiva laddningar i vätskan har en hastighetsvektor som pekar nedåt. Kraften på vätskan är ute av sidan. En illustration av höger regel 1 visar tummen som pekar nedåt med strömmen, fingrarna pekar åt höger med B och tvinga F orienterad ut ur sidan, bort från handflatan.
Figur 3. Magnetohydrodynamik. Den magnetiska kraften på strömmen som passerar genom denna vätska kan användas som en icke-mekanisk pump.

ett starkt magnetfält appliceras över ett rör och en ström passerar genom vätskan i rät vinkel mot fältet, vilket resulterar i en kraft på vätskan parallellt med röraxeln som visas. Frånvaron av rörliga delar gör detta attraktivt för att flytta en het, kemiskt aktiv substans, såsom det flytande natrium som används i vissa kärnreaktorer. Experimentella konstgjorda hjärtan testar med denna teknik för att pumpa blod, kanske kringgå de negativa effekterna av mekaniska pumpar. (Cellmembran påverkas emellertid av de stora fält som behövs i MHD, vilket fördröjer dess praktiska tillämpning hos människor.) MHD-framdrivning för atomubåtar har föreslagits, eftersom det kan vara betydligt tystare än konventionella propellerdrivningar. Det avskräckande värdet av atomubåtar är baserat på deras förmåga att dölja och överleva en första eller andra kärnvapenstrejk. När vi sakta demonterar våra kärnvapenarsenaler kommer ubåtsgrenen att vara den sista som avvecklas på grund av denna förmåga (Se figur 4.) Befintliga MHD-enheter är tunga och ineffektiva—mycket utvecklingsarbete behövs.

Diagram som visar en zoom in i ett magnetohydrodynamiskt framdrivningssystem på en atomubåt. Vätska rör sig genom propellerkanalen, som är orienterad ut ur sidan. Magnetfält kommer ut från spolarna och passerar genom en kanal. Det magnetiska flödet är orienterat uppåt, vinkelrätt mot kanalen. Varje kanal är insvept i sadelformade superledande spolar. En elektrisk ström går åt höger, genom vätskan och vinkelrätt mot vätskans hastighet. Den elektriska strömmen strömmar mellan ett par elektroder inuti varje propellerkanal. En repulsiv interaktion mellan magnetfältet och elektrisk ström driver vatten genom kanalen. En illustration av högerhandsregeln visar tummen som pekar åt höger med den elektriska strömmen. Fingrarna pekar upp med magnetfältet. Kraften på vätskan är orienterad ut ur sidan, bort från handflatan.
Figur 4. Ett MHD-framdrivningssystem i en atomubåt kan producera betydligt mindre turbulens än propellrar och låta det gå tystare. Utvecklingen av en tyst enhet ubåt dramatiserades i boken och filmen Jakten på Röd Oktober.
  • den magnetiska kraften på strömbärande ledare ges av
    \boldsymbol{F = IlB \;\textbf{sin} \;\theta},

    där \boldsymbol{i} är strömmen, \boldsymbol{l} är längden på en rak ledare i ett enhetligt magnetfält \boldsymbol{B}, och \boldsymbol{\theta} är vinkeln mellan \boldsymbol{i} och \boldsymbol{B}. Kraften följer RHR-1 med tummen i riktning mot \ boldsymbol{i}.

konceptuella frågor

1: Rita en skiss av situationen i Figur 1 som visar riktningen för elektroner som bär strömmen och använd RHR-1 för att verifiera kraftens riktning på tråden.

2: Kontrollera att kraftens riktning i en MHD-enhet, såsom den i Figur 3, inte beror på tecknet på laddningarna som bär strömmen över vätskan.

3: Varför skulle en magnetohydrodynamisk enhet fungera bättre i havsvatten än i färskvatten? Varför skulle superledande magneter vara önskvärda?

4: Vilket är mer sannolikt att störa kompassavläsningar, växelström i ditt kylskåp eller likström när du startar bilen? Förklara.

problem & övningar

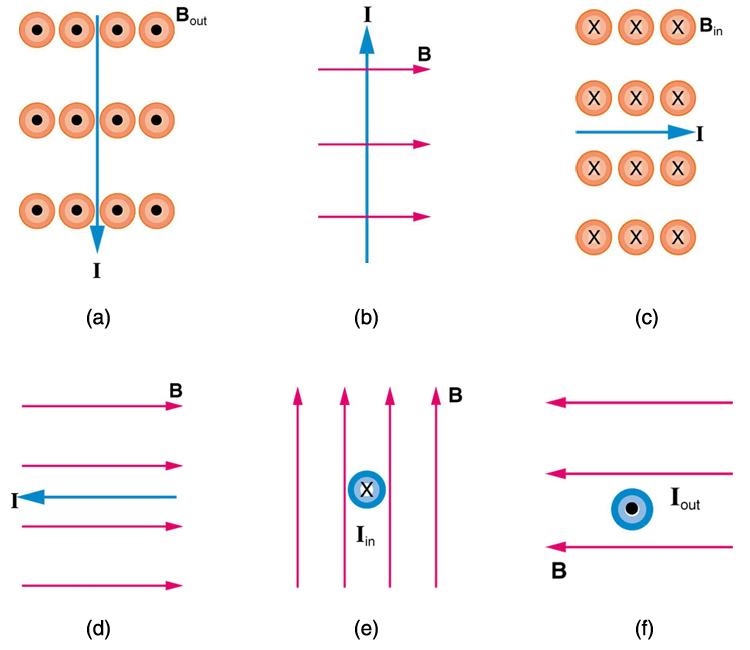
1: Vad är riktningen för den magnetiska kraften på strömmen i vart och ett av de sex fallen i Figur 5?

Figur A visar magnetfältet B från sidan och strömmen i nedåt. Figur b visar B åt höger och jag uppåt. Figur c visar B på sidan och jag åt höger. Figur d visar B mot höger och jag mot vänster. Figur E visar B uppåt och jag in på sidan. Figur f visar B åt vänster och jag ut ur sidan.
Figur 5.

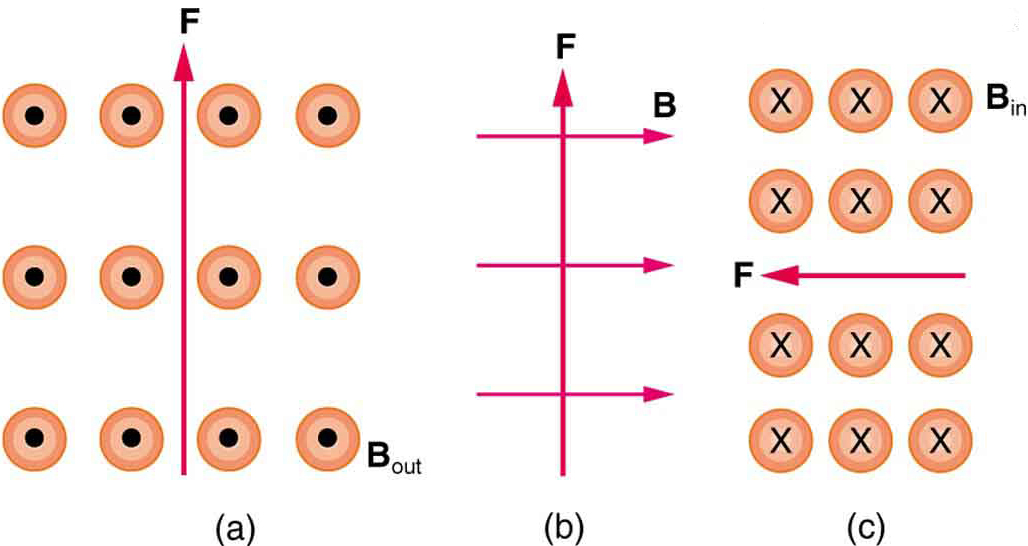
2: Vad är riktningen för en ström som upplever den magnetiska kraften som visas i vart och ett av de tre fallen i Figur 6, förutsatt att strömmen går vinkelrätt mot \boldsymbol{B}?

Figur A visar magnetfält B från sidan och tvingar F uppåt. Figur b visar B mot höger och F uppåt. Figur c visar B på sidan och F åt vänster.
Figur 6

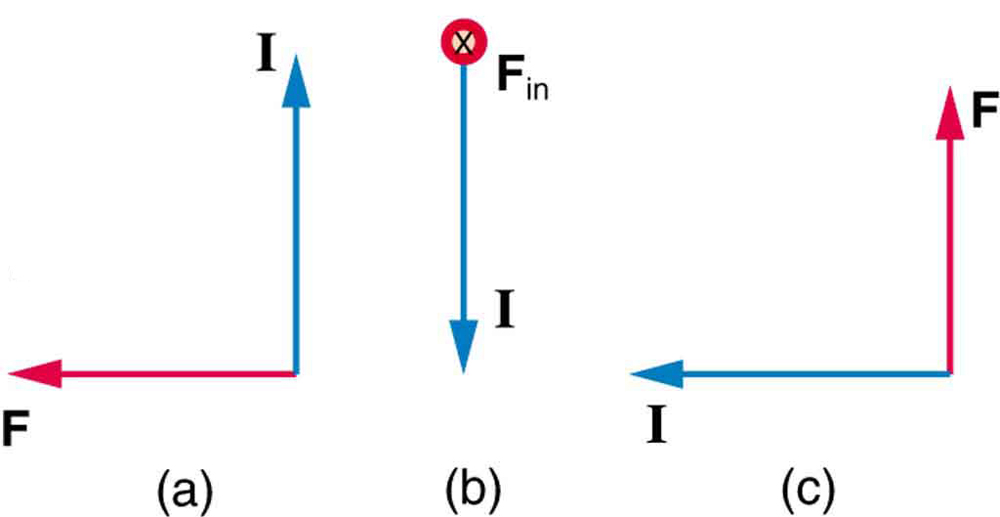
3: Vad är magnetfältets riktning som producerar den magnetiska kraft som visas på strömmarna i vart och ett av de tre fallen i Figur 7, förutsatt att \boldsymbol{B} är vinkelrätt mot \boldsymbol{i}?

Figur A visar den aktuella i-vektorn som pekar uppåt och kraften F-vektorn pekar åt vänster. Figur b visar den aktuella vektorn som pekar nedåt och f riktad in på sidan. Figur c visar den aktuella pekar åt vänster och kraft pekar uppåt.
Figur 7.

4: (A) Vad är kraften per meter på en blixtbult vid ekvatorn som bär 20 000 a vinkelrätt mot jordens \boldsymbol{3.00 \gånger 10^{-5} – \textbf{t}} fält? (B) Vad är kraftens riktning om strömmen är rakt upp och jordens fältriktning är rakt norrut, parallellt med marken?

5: (a) en LIKSTRÖMSLEDNING för ett spårvägssystem bär 1000 A i en vinkel på \boldsymbol{30.0 ^{\circ}} till jordens \boldsymbol{5.00 \gånger 10^{-5}-\textbf{t}} fält. Vad är kraften på en 100 m sektion av denna linje? (B) diskutera praktiska frågor som detta presenterar, om någon.

6: Vilken kraft utövas på vattnet i en MHD-enhet som använder ett rör med 25,0 cm diameter, om 100-en ström passerar över röret som är vinkelrätt mot ett 2,00-t magnetfält? (Den relativt lilla storleken på denna kraft indikerar behovet av mycket stora strömmar och magnetfält för att göra praktiska MHD-enheter.)

7: en tråd som bär en 30.0-A-ström passerar mellan polerna på en stark magnet som är vinkelrätt mot sitt fält och upplever en 2.16-n-kraft på 4.00 cm tråd i fältet. Vad är den genomsnittliga fältstyrkan?

8: (a) en 0,750 m lång sektion av kabel som bär ström till en bilstartmotor gör en vinkel på \boldsymbol{60^{\circ}} med jordens \boldsymbol{5,50 \gånger 10^{-5} \;\textbf{t}} fält. Vad är strömmen när tråden upplever en kraft av \ boldsymbol{7.00 \ gånger 10^{-3}\; \ textbf{N}}? (b) om du kör tråden mellan polerna på en stark hästskomagnet och utsätter 5,00 cm av den för ett 1,75-t-fält, vilken kraft utövas på detta segment av tråd?

9: (A) Vad är vinkeln mellan en tråd som bär en 8.00-A-ström och 1.20-t-fältet det är i om 50.0 cm av tråden upplever en magnetisk kraft på 2.40 n? (b) Vad är kraften på tråden om den roteras för att göra en vinkel på \boldsymbol{90^{\circ}} med fältet?

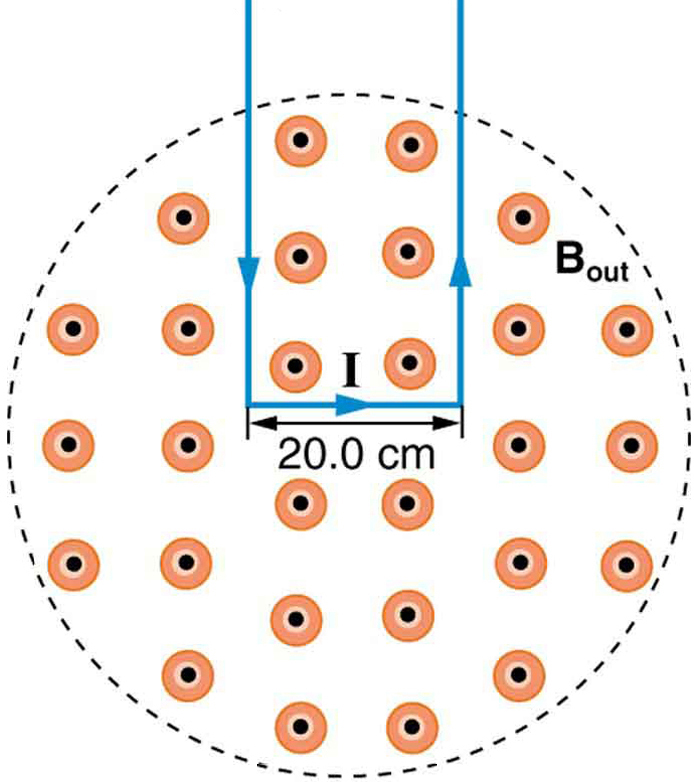
10: kraften på den rektangulära trådslingan i magnetfältet i Figur 8 kan användas för att mäta fältstyrkan. Fältet är enhetligt och slingans plan är vinkelrätt mot fältet. (A) Vad är riktningen för den magnetiska kraften på slingan? Motivera påståendet att krafterna på slingans sidor är lika och motsatta, oberoende av hur mycket av slingan som finns i fältet och inte påverkar nätkraften på slingan. (b) om en ström på 5,00 A används, vad är kraften per tesla på den 20,0 cm breda slingan?

Diagram som visar en rektangulär slinga av tråd, vars ena ände ligger inom ett magnetfält som finns inom ett cirkulärt område. Fältet B är orienterat från sidan. Strömmen jag kör i sidans plan, ner till vänster om kretsen, mot höger längst ner på kretsen och uppåt på höger sida av kretsen. Längden på segmentet av tråd som löper från vänster till höger längst ner på kretsen är tjugo centimeter lång.
figur 8.

lösningar

problem & övningar

1: (A) väst (vänster)

(b) till sidan

(c) norr (upp)

(d) ingen kraft

(e) öst (höger)

(f) söder (ner)

3: (A) in i sidan

(b) väst (vänster)

(c) ut ur sidan

5: (a) 2.50 n

(b) Detta är ungefär ett halvt pund kraft per 100 m tråd, vilket är mycket mindre än själva trådens vikt. Därför orsakar det inga speciella problem.

7: 1, 80 T

9: (a) \ fetsymbol{30^{\circ}}

(b) 4,80 N