nedenstående artikel giver et tæt overblik over Cobb-Douglas produktionsfunktionen. Cobb-Douglas produktionsfunktionen er baseret på den empiriske undersøgelse af den amerikanske fremstillingsindustri lavet af Paul H. Douglas og Cobb. Det er en lineær homogen produktionsfunktion af grad en, der tager højde for to input, arbejdskraft og kapital, for hele produktionen af .fremstillingsindustri. Cobb-Douglas produktionsfunktionen udtrykkes som:

K = Ala C-L

hvor K er output og L og L er input af henholdsvis arbejdskraft og kapital. A, A og KR er positive parametre, hvor = a > O, KRH > O.

ligningen fortæller, at output afhænger direkte af L og C, og den del af output, der ikke kan forklares med L og KRH, forklares med A, som er den ‘resterende’, ofte kaldet teknisk ændring.

produktionsfunktionen løst af Cobb-Douglas havde 1/4 kapitalbidrag til stigningen i fremstillingsindustrien og 3/4 af arbejdskraft, således at C-D produktionsfunktionen er

K = AL3/4 C1/4

som viser konstant afkast til skala, fordi summen af værdierne for L og KR er lig med en: (3/4 + 1/4), dvs. (a + list = 1). Arbejderens koefficient i C-D-funktionen måler den procentvise stigning i (K, der ville være resultatet af en stigning på 1 procent i L, mens man holder Lr som konstant.

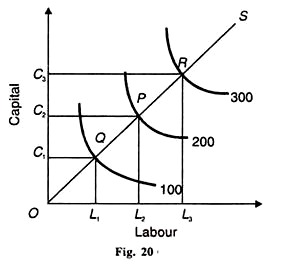
tilsvarende er den procentvise stigning i K, der ville være resultatet af en stigning på 1 procent i C, mens L holdes som konstant. C – D-produktionsfunktionen, der viser konstant retur til skala, er afbildet i Figur 20. Arbejdskraftinput tages på den vandrette akse og kapital på den lodrette akse.

til fremstilling af 100 produktionsenheder anvendes der i alt kr., kapitalenheder og arbejdsenheder. Hvis produktionen skulle fordobles til 200, skulle tilførslen af arbejdskraft og kapital fordobles. Det er dobbelt så meget som det 1. og OL2 er dobbelt så meget som OL2.

tilsvarende, hvis produktionen skal hæves tre gange til 300, skal arbejdsenhederne og kapitalen øges tre gange. OC3 og OL3 er tre gange større end henholdsvis kr1 og OL1. En anden metode er at tage skalalinjen eller udvidelsesstien, der forbinder ligevægtspunkterne K, P og R. OS er skalalinjen eller udvidelsesstien, der forbinder disse punkter.

det viser, at isokvanterne 100, 200 og 300 er lige langt. På OS-skalalinjen viser det sig således, at når kapital og arbejdskraft øges i lige store andele, stiger produktionen også i samme forhold.

kritik af C – D produktionsfunktion:

C-d produktionsfunktionen er blevet kritiseret af pil, Chenery, Minhas og Solov som diskuteret nedenfor:

1. Cd-produktionsfunktionen betragter kun to input, arbejdskraft og kapital, og forsømmer nogle vigtige input, som råmaterialer, der bruges i produktionen. Det er derfor ikke muligt at generalisere denne funktion til mere end to indgange.

2. I cd-produktionsfunktionen opstår problemet med måling af kapital, fordi det kun tager den mængde kapital, der er til rådighed til produktion. Men den fulde udnyttelse af den disponible kapital kan kun ske i perioder med fuld beskæftigelse. Dette er urealistisk, fordi ingen økonomi altid er fuldt beskæftiget.

3. C – D-produktionsfunktionen kritiseres, fordi den viser konstant tilbagevenden til skala. Men konstant afkast til skala er ikke en realitet, for enten stigende eller faldende afkast til skala gælder for produktion.

det er ikke muligt at ændre alle input for at bringe en forholdsmæssig ændring i output fra alle brancher. Nogle input er knappe og kan ikke øges i samme forhold som rigelige input. På den anden side input som maskiner, iværksætteri osv. er udelelige. Da produktionen stiger på grund af brugen af udelelige faktorer til deres maksimale kapacitet, falder omkostningerne pr.

når tilførslen af input er knappe og udelelighed er til stede, er konstant tilbagevenden til skala ikke mulig. Når enhederne med forskellige input øges i produktionsprocessen, fører stordriftsfordele og specialisering til stigende afkast til skala.

i praksis vil ingen iværksætter dog gerne øge de forskellige enheder af input for at få en forholdsmæssig stigning i produktionen. Hans bestræbelser er at have en mere end forholdsmæssig stigning i produktionen, selvom faldende afkast til skala heller ikke udelukkes.

4. C – D-produktionsfunktionen er baseret på antagelsen om substituerbarhed af faktorer og forsømmer komplementariteten af faktorer.

5. Denne funktion er baseret på antagelsen om perfekt konkurrence på faktormarkedet, hvilket er urealistisk. Hvis denne antagelse imidlertid bortfalder, repræsenterer koefficienterne kr.og kr. ikke faktoraktier.

6. En af svaghederne ved C – D-funktionen er aggregeringsproblemet. Dette problem opstår, når denne funktion anvendes på alle virksomheder i en industri og til hele branchen. I denne situation vil der være mange produktionsfunktioner med lav eller høj aggregering. C – D-funktionen måler således ikke, hvad den sigter mod at måle.

konklusion:

således er gennemførligheden af C-D-produktionsfunktionen i fremstillingsindustrien et tvivlsomt forslag. Dette gælder ikke for landbrug, hvor en forøgelse af mængden af input til intensiv dyrkning ikke vil øge produktionen forholdsmæssigt. Selv da kan det ikke nægtes, at konstant tilbagevenden til skala er et stadium i en virksomheds, industris eller økonomis liv. Det er en anden ting, at denne fase kan komme efter et stykke tid og i et kort stykke tid.

det er vigtigt:

På trods af denne kritik er C-D-funktionen meget vigtig.

1. Det er blevet brugt bredt i empiriske undersøgelser af fremstillingsindustrier og i sammenligninger mellem industrien.

2. Det bruges til at bestemme de relative andele af arbejdskraft og kapital i den samlede produktion.

3. Det bruges til at bevise Eulers sætning.

4. Dens parametre A og b repræsenterer elasticitetskoefficienter, der anvendes til tværsektorielle sammenligninger.

5. Denne produktionsfunktion er lineær homogen af grad en, der viser konstant afkast til skala, hvis prisT + prisT = 1, er der stigende afkast til skala, og hvis prisT + prisT < 1, er der faldende afkast til skala.

6. Økonomer har udvidet denne produktionsfunktion til mere end to variabler.