en tensor er en række data (tal, funktioner osv.), som udvides i et hvilket som helst antal (0 og større) af dimensioner. Antallet af dimensioner kaldes rang af tensor.

rang 0 tensor

en tensor, der ikke har dimensioner (0).

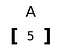
rang 1 tensor

en tensor, der kun udvides i en dimension.

Rank 2 tensor

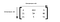
Rank 3 tensor

As shown in figure, a rank 3 tensor has a cube (or cuboid like structure).

If rank of a tensor exceeds 3, it becomes difficult to visualize.

Scalar

en skalar er 0 rang tensor. I fysik er forskellige mængder repræsenteret som en skalar, såsom : afstand (500 km), temperatur (10 liter), hastighed (34 km/t) osv.

vektor

en rang 1 tensor kaldes en vektor. Fysiske størrelser såsom hastighed (10 m/s), forskydning (54 m mod øst), elektromagnetisk felt (1 V/m).

forskel mellem skalar og vektor :

en mængde, der ikke kræver yderligere oplysninger (såsom retning) med den (som temperatur) er repræsenteret som skalar. Mens en mængde, der har brug for retning, der skal specificeres sammen med dens størrelse, er repræsenteret med en vektor (som elektrisk felt).

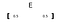
en vektor er betegnet med fed skrift (som “E” ) eller en pil over brevet.

for at plotte en vektor bruger vi dens elementer som værdien af koordinater (hhv. Her tages første element (0,5) som værdi og andet element (også 0,5) som Y-værdi (hvis vi havde tre elementer, ville den tredje have været værdi).

efter at have tegnet vektoren som et punkt sætter vi en pil til den, fra Oprindelse(0,0).

en vektor er simpelthen en matrice, der har enten en række (kaldet kolonnevektor) eller en kolonne (kaldet rækkevektor).

Matrice

en matrice er en rang 2 tensor. Vi har set på matricen tidligere.

en tensor med rang større end 2 kaldes simpelthen “tensor” (der er ikke noget specifikt navn for tensorer med rang mere end 2).

begrebet tensor generaliserer matricer, vektorer og skalarer under et tag (de er alle tensorer, men med forskellige rækker).

matricer som produkt af vektorer:

når to vektorer multipliceres, danner de en matrice.

Vector X and Y combined, have 6 elements but their product alone has 9 elements. Således kunne nogle matricer nedbrydes som et produkt af to vektorer.