Funktionsnotation og hvordan man evaluerer en funktion
den fælles notation af en funktion skrives normalt som
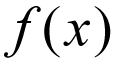
tænk ikke på dette for bogstaveligt, det vil sige, f multipliceres til H. Overvej i stedet dette som et matematisk udtryk, der læses som
eller
funktioner kan også skrives på forskellige måder ved hjælp af andre variabler som
- G(H), H(H) og K(H)
desuden kan Funktioner tage
- f(A), h(r) og k(m)
inputværdien af funktionen.
for eksempel kaldes følgende funktion k med en inputværdi på m.
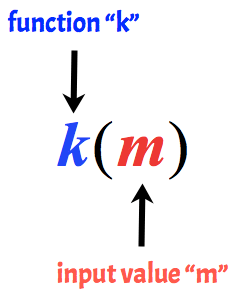
grundlæggende eksempler på evaluering af funktioner
eksempel 1: Evaluer funktionen .
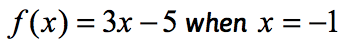
dette er den normale notation af funktion, hvor funktionen er f, mens inputværdien er H. for at evaluere en funktion, er det, vi ønsker, at erstatte en funktion, der er i udtrykket og derefter forenkle.
siden H = – 1 erstatter vi denne værdi i funktionen og forenkler. På den måde får vi en løsning, der ser sådan ud.
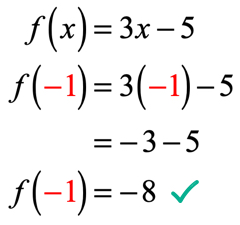
eksempel 2: Evaluer funktionen .
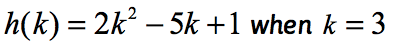
Vær opmærksom på, at funktionen her er h, og inputværdien er k. Ligesom i vores tidligere eksempel ønsker vi at erstatte den numeriske værdi, der er tildelt k, i den givne funktion og forenkle.
siden k = 3, skal din løsning se ud som denne
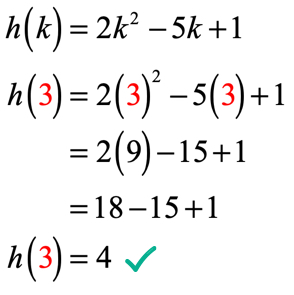
eksempel 3: Evaluer hver værdi i tabellen nedenfor ved hjælp af funktionen nedenfor. Tegn punkterne i aksen, og Forbind prikkerne for at afsløre grafen for funktionen.
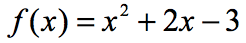
da der er syv indgange, betyder det, at vi også vil evaluere funktionen syv gange. Prøv at arbejde dette ud på egen hånd, så kom tilbage for at tjekke dine svar.
Hvis du har gjort det korrekt, er det værdierne:
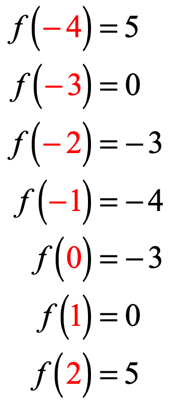
Vi kan nu placere disse outputværdier i tabellen.
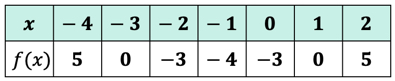
tænk på outputværdierne for funktionen f\venstre( h \højre) som y-værdierne. Sådan ser grafen ud på aksen.
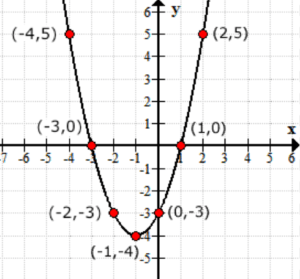-3 og h-aflytninger af -3 og 1.mellemliggende eksempler på evaluering af funktioner
eksempel 4: i betragtning af at g\left( h \right) = {H^2} – 3 gange + 1, find g\left( {2h – 1} \right).
i tidligere eksempler har vi evalueret en funktion Med et tal. Denne gang er inputværdien ikke længere en fast numerisk værdi, men i stedet et udtryk. Det kan se kompliceret ud, men proceduren forbliver den samme.
Vi erstatter alle forekomster af H i g\venstre( h \højre) med inputværdien, som er 2H – 1. Forenkle ved at kvadrere binomialet, anvende den distributive egenskab og kombinere lignende udtryk.
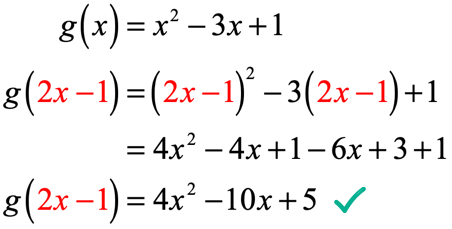
eksempel 5: i betragtning af at p\left (højre) = {{4 gange-1} \over} , evaluer p \left (1\right) – p \left ({- 1}\right).
problemet kan se skræmmende ud i starten, men når vi først analyserer det og anvender det, vi allerede ved, hvordan vi evaluerer funktioner, bør dette ikke være så slemt!
hvad vi skal gøre her er at evaluere funktionen ved H = 1 og derefter trække med værdien af funktionen,når den evalueres ved H= -\, 1.
Vær meget forsigtig, når du erstatter værdierne og under forenklingsprocessen. Hvis du ikke er forsigtig i hvert trin, er det meget let at begå fejl, når du tilføjer, trækker, multiplicerer eller deler positive og negative tal.
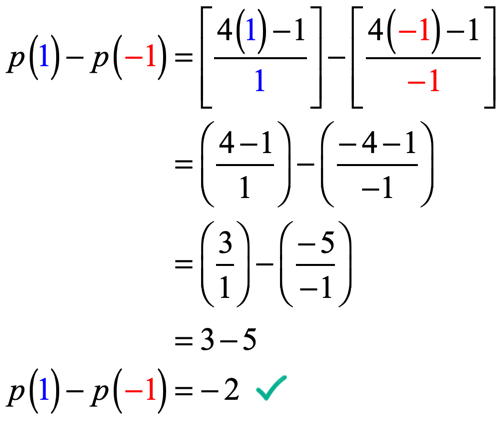
avanceret eksempel på anvendelse af begrebet Evalueringsfunktioner
eksempel 6: hvis f\left( 2 \right) = 9, find værdien af A i funktionen nedenfor.
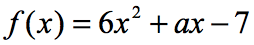
i ligningen, f\left( 2 \right) = 9, får vi at vide, at hvis indgangen til den nye funktionen er 2; udgangen af funktionen vil være 9. Da funktionen er givet til os, er vores første skridt i det mindste at erstatte værdien af 2 og derefter forenkle. Dette er, hvad vi får.
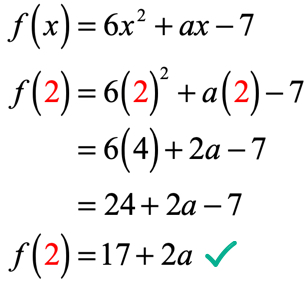
funktionens output efter evaluering ved H = 2 er 17 + 2a. Husk, at vi også får at vide, at udgangen er 9 ved hjælp af den givne ligning f\venstre( 2 \højre) = 9. Derfor er det, vi skal gøre nu,at sætte dem lig med hinanden og løse den lineære ligning for den ukendte værdi af a.
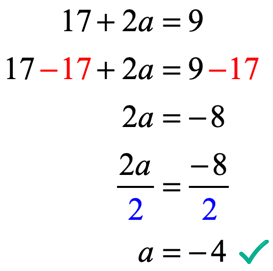
lad os kontrollere, om værdien af A= -\, 4 i F(H) = 6{H^2} + økse – 7 kan gøre den givne betingelse f\venstre( 2 \højre) = 9 for at være en sand erklæring.
det er sandt! Derfor har vi med succes løst for den korrekte værdi af A.
Leave a Reply