Articles

fysik

by admin

Vi ved fra kinematik, AT acceleration er en ændring i hastighed, enten i dens størrelse eller i dens retning eller begge dele. I ensartet cirkulær bevægelse ændres hastighedsretningen konstant, så der er altid en tilknyttet acceleration, selvom størrelsen af hastigheden kan være konstant. Du oplever denne acceleration selv, når du drejer et hjørne i din bil. (Hvis du holder hjulet stabilt under en tur og bevæger dig med konstant hastighed, er du i ensartet cirkulær bevægelse.) Hvad du bemærker er en sidelæns acceleration, fordi du og bilen ændrer retning. Jo skarpere kurven og jo større din hastighed er, desto mere mærkbar bliver denne acceleration. I dette afsnit undersøger vi retningen og størrelsen af denne acceleration.

Figur 1 viser et objekt, der bevæger sig i en cirkulær bane med konstant hastighed. Retningen af den øjeblikkelige hastighed er vist på to punkter langs stien. Acceleration er i retning af hastighedsændringen, som peger direkte mod rotationscentret (midten af den cirkulære sti). Denne peger er vist med vektordiagrammet i figuren. Vi kalder accelerationen af et objekt, der bevæger sig i ensartet cirkulær bevægelse (som følge af en netto ekstern kraft) centripetal acceleration(ac); centripetal betyder “mod midten” eller “center søger.”

den givne figur viser en cirkel med en trekant med hjørner A B C lavet fra midten til grænsen. A er i centrum, og B og C punkter er på cirkelstien. Linjer A B og A C fungerer som radier og B C er en akkord. Delta theta er vist inde i trekanten, og buelængden delta s og akkordlængden delta r er også angivet. Ved punkt B vises objektets hastighed som v en og ved punkt C vises objektets hastighed som V to. Langs cirklen vises en ligning som delta v er lig med V sub 2 minus v sub 1.

Figur 1. Retningerne for hastigheden af et objekt på to forskellige punkter er vist, og ændringen i hastighedslyster ses at pege direkte mod krumningscentret. (Se lille indsats.) Fordi ac = KRP / KRP, accelerationen er også mod midten; ac kaldes centripetal acceleration. (Fordi kursen er meget lille, er buelængden kursen lig med akkordlængden kurren for små tidsforskelle.)

retningen af centripetal acceleration er mod krumningscentret, men hvad er dens størrelse? Bemærk, at trekanten dannet af hastighedsvektorerne og den, der er dannet af radierne r og kryss, er ens. Begge trekanter ABC og PKR er ligebenede trekanter (to lige sider). De to lige sider af hastighedsvektortrekanten er hastighederne v1 = v2 = v. Ved hjælp af egenskaberne for to lignende trekanter opnår vi \frac{\Delta{v}}{v}=\frac{\Delta{s}}{r}\\.

Acceleration er \frac {\Delta{v}} {\Delta{t}}\\, og så løser vi først dette udtryk for Pristv:

\displaystyle\Delta{v}=\frac{v}{r}\Delta{s}\\.

så deler vi dette med prit, hvilket giver

\displaystyle\frac{\Delta{v}}{\Delta{t}}=\frac{v}{r}\times\frac{\Delta{s}}{\Delta{t}}\\.

endelig bemærker vi, at \frac{\Delta{v}}{\Delta{t}}=a_c\\ og at \frac{\Delta{s}}{\Delta{t}}=v\\, den lineære eller tangentielle hastighed, vi ser, at størrelsen af centripetal acceleration er

{a}_c=\frac{v^2}{r}\\,

hvilket er accelerationen af et objekt i en cirkel med radius r ved en hastighed v. Så centripetal acceleration er større ved høje hastigheder og i skarpe kurver (mindre radius), som du har bemærket, når du kører bil. Men det er lidt overraskende, at ac er proportional med hastigheden i kvadrat, hvilket for eksempel antyder, at det er fire gange så svært at tage en kurve ved 100 km/t end ved 50 km/t. et skarpt hjørne har en lille radius, så ac er større for strammere sving, som du sandsynligvis har bemærket.

det er også nyttigt at udtrykke ac med hensyn til vinkelhastighed. Ved at erstatte v = RV i ovenstående udtryk finder vi a_c=\frac{\left(r\omega\right)^2}{r}=R\omega^2\\. Vi kan udtrykke størrelsen af centripetal acceleration ved hjælp af en af to ligninger:

\displaystyle{a}_c=\frac{v^2}{r}; a_c=r\omega^2\\.

Husk at retningen af ac er mod midten. Du kan bruge det udtryk, der er mere praktisk, som illustreret i eksemplerne nedenfor.

en centrifuge (se figur 2B) er en roterende enhed, der bruges til at adskille prøver med forskellige tætheder. Høj centripetal acceleration reducerer signifikant den tid, det tager for adskillelse at forekomme, og muliggør adskillelse med små prøver. Centrifuger anvendes i en række anvendelser inden for videnskab og medicin, herunder adskillelse af enkeltcellesuspensioner såsom bakterier, vira og blodlegemer fra et flydende medium og adskillelse af makromolekyler, såsom DNA og protein, fra en opløsning. Centrifuger vurderes ofte med hensyn til deres centripetal acceleration i forhold til acceleration på grund af tyngdekraften (g); maksimal centripetal acceleration på flere hundrede tusinde g er mulig i et vakuum. Menneskelige centrifuger, ekstremt store centrifuger, er blevet brugt til at teste astronauternes tolerance over for virkningerne af accelerationer, der er større end Jordens tyngdekraft.

eksempel 1. Hvordan sammenligner Centripetalaccelerationen af en bil omkring en kurve med den på grund af tyngdekraften?

Hvad er størrelsen af den centripetale acceleration af en bil efter en kurve med radius 500 m ved en hastighed på 25,0 m/s (ca. 90 km/t)? Sammenlign accelerationen med den på grund af tyngdekraften for denne ret blide kurve taget ved motorvejshastighed. Se figur 2a.

strategi

fordi v og r er givet, er det første udtryk i \displaystyle{a}_c=\frac{v^2}{r}; a_c=r\omega^2\\ det mest praktiske at bruge.

opløsning

indtastning af de givne værdier af v = 25,0 m/s og r=500 m i det første udtryk for ac giver

\displaystyle{a}_c=\frac{v^2}{r}=\frac{\venstre(25,0\tekst{ m/s}\højre)^2}{500\tekst{ m}}=1,25\tekst{ m/s}^2\\.

Diskussion

for at sammenligne dette med accelerationen på grund af tyngdekraften (g = 9,80 m / s2) tager vi forholdet mellem \displaystyle\frac{a_c}{g}=\frac{\left(1.25 \ tekst{ m/s}^2\højre)}{\venstre(9.80\tekst{ m / s}^2\højre)}=0.128\\. Således ac=0,128 g og er mærkbar, især hvis du ikke havde sikkerhedssele.

i Figur A kører en bil vist fra toppen på en cirkulær vej omkring en cirkulær sti. Parkens centrum betegnes som centrum for denne cirkel, og afstanden fra dette punkt til bilen tages som radius r. Den lineære hastighed er vist i vinkelret retning mod fronten af bilen, vist som v den centripetale acceleration er vist med en pil peget mod rotationscentret. I figur b, en centrifuge er vist et objekt af masse m roterer i det med en konstant hastighed. Objektet er i afstanden lig med centrifugens radius, r. Den centripetale acceleration er vist mod rotationscentret, og hastigheden, v er vist vinkelret på objektet i urets retning.

figur 2. (a) bilen, der følger en cirkulær bane med konstant hastighed, accelereres vinkelret på dens hastighed, som vist. Størrelsen af denne centripetal acceleration findes i Eksempel 1. (b) en partikel af masse i en centrifuge roterer med konstant vinkelhastighed . Det skal accelereres vinkelret på dets hastighed, ellers fortsætter det i en lige linje. Størrelsen af den nødvendige acceleration findes i Eksempel 2.

eksempel 2. Hvor stor er Centripetal accelerationen i en Ultracentrifuge?

Beregn centripetal acceleration af et punkt 7.50 cm fra aksen af en ultracentrifuge spinding ved 7,5 liter 104 omdr/min. Bestem forholdet mellem denne acceleration og det på grund af tyngdekraften. Se figur 2b.

strategi

udtrykket rev / min står for omdrejninger pr.minut. Ved at konvertere dette til radianer pr. Fordi r er givet, kan vi bruge det andet udtryk i ligningen a_c=\frac{v^2}{r};a_c=r\omega^2\\ til at beregne centripetal acceleration.

opløsning

for at konvertere 7.50 liter 104 omdr/min til radianer per sekund, vi bruger de kendsgerninger, at en revolution er 2 liter rad og et minut er 60,0 s. således

\displaystyle\omega=7.50\times10^4\frac{\text{rev}}{\text{min}}\times\frac{2\pi\text{ rad}}{1 \ tekst{ rev}} \ gange\frac{1\Tekst{ min}}{60.0\tekst{ s}}=7854\ tekst{ rad/s}\\.

nu er centripetalaccelerationen givet ved det andet udtryk i

\displaystyle{a}_c=\frac{v^2}{r}; a_c=r\omega^2\\ som ac = RV2.

konvertering af 7,50 cm til meter og udskiftning af kendte værdier giver ac = (0,0750 m)(7854 rad/s)2 = 4.63 til 106 m/s2.

Bemærk, at de unitless radianer kasseres for at få de korrekte enheder til centripetal acceleration. At tage forholdet mellem ac og g giver

\frac{a_c}{g}=\frac{4.63\times10^6}{9.80}=4.72\times10^5\\.

Diskussion

dette sidste resultat betyder, at centripetalaccelerationen er 472.000 gange så stærk som g. det er ikke underligt, at sådanne højkoloncentrifuger kaldes ultracentrifuger. De ekstremt store accelerationer involveret reducerer i høj grad den tid, der er nødvendig for at forårsage sedimentering af blodlegemer eller andre materialer.selvfølgelig er der brug for en netto ekstern kraft for at forårsage enhver acceleration, ligesom han foreslog i sin anden bevægelseslov. Så en netto ekstern kraft er nødvendig for at forårsage en centripetal acceleration. I Centripetal kraft vil vi overveje de kræfter, der er involveret i cirkulær bevægelse.

PhET-udforskninger: Ladybug Motion 2D

Lær om position, hastighed og accelerationsvektorer. Flyt mariehøne ved at indstille position, hastighed eller acceleration, og se, hvordan vektorerne ændres. Vælg lineær, cirkulær eller elliptisk bevægelse, og optag og afspil bevægelsen for at analysere adfærden.

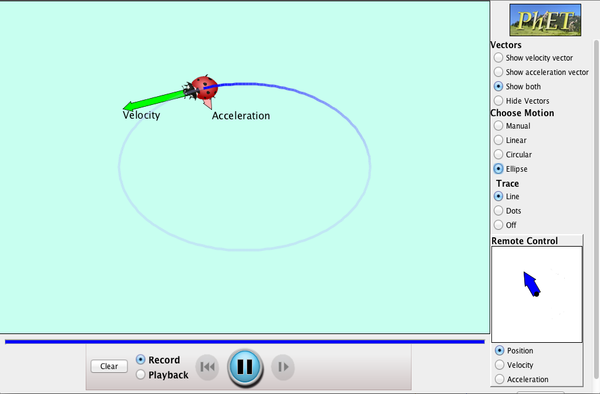
Ladybug Motion 2D screenshot.

Klik på billedet for at hente. Brug Java til at køre simuleringen.

Sektionsoversigt

  • Centripetal acceleration ac er den acceleration, der opleves i ensartet cirkulær bevægelse. Det peger altid mod rotationscentret. Den er vinkelret på den lineære hastighed v og har størrelsen {a}_{\Tekst{c}}=\frac{{v}^{2}}{r}; {a}_{\Tekst{c}}={\mathrm{r\omega }}^{2}\\.
  • enheden for centripetal acceleration er m / s2.

konceptuelle spørgsmål

  1. kan centripetal acceleration ændre hastigheden af cirkulær bevægelse? Forklare.

problemer& øvelser

  1. en tivolitur drejer sine beboere inde i en flyvende tallerkenformet beholder. Hvis den vandrette cirkulære sti, som rytterne følger, har en radius på 8,00 m, hvor mange omdrejninger pr. minut vil rytterne blive udsat for en centripetal acceleration, hvis størrelse er 1,50 gange den på grund af tyngdekraften?
  2. en løber, der deltager i 200 m dash, skal løbe rundt om enden af et spor, der har en cirkulær bue med en krumningsradius på 30 m. hvis han afslutter 200 m dash på 23,2 s og kører med konstant hastighed gennem hele løbet, hvad er størrelsen af hans centripetal acceleration, når han kører den buede del af banen?
  3. tager Jordens alder til at være omkring 4 liter 109 år og antager sin kredsløbsradius på 1.5. 1011 har ikke ændret sig og er cirkulær, beregne den omtrentlige samlede afstand Jorden har rejst siden sin fødsel (i en referenceramme stationær i forhold til Solen).
  4. propellen til et Anden Verdenskrigs kampfly er 2,30 m i diameter. (A) Hvad er dens vinkelhastighed i radianer pr. sekund, hvis den drejer ved 1200 omdr/min? (b) Hvad er den lineære hastighed af dens spids ved denne vinkelhastighed, hvis flyet står stille på asfalten? (c) Hvad er den centripetale acceleration af propelspidsen under disse forhold? Beregn det i meter per sekund kvadreret og konverter til multipla af g.
  5. en almindelig værksted slibesten har en radius på 7,50 cm og roterer ved 6500 omdr/min. (a) beregne størrelsen af den centripetale acceleration ved dens kant i meter pr. sekund kvadreret og konvertere den til multipla af g. (b) Hvad er den lineære hastighed for et punkt på dets kant?
  6. helikopterblade modstår enorme belastninger. Ud over at understøtte vægten af en helikopter spindes de i hurtige hastigheder og oplever store centripetale accelerationer, især ved spidsen. (A) Beregn størrelsen af den centripetale acceleration ved spidsen af et 4,00 m langt helikopterblad, der roterer ved 300 omdr/min. B) sammenligne spidsens lineære hastighed med lydens hastighed (beregnet til at være 340 m/s).
  7. Olympiske skøjteløbere er i stand til at dreje omkring 5 omdr/s. (A) Hvad er deres vinkelhastighed i radianer pr. sekund? (b) Hvad er den centripetale acceleration af skaterens næse, hvis den er 0,120 m fra rotationsaksen? (c) en ekstraordinær skater ved navn Dick Button var i stand til at dreje meget hurtigere i 1950 ‘ erne end nogen siden—på omkring 9 omdr/s. Hvad var centripetalaccelerationen af næsespidsen, forudsat at den er ved 0, 120 m radius? D) kommentere størrelsen af de konstaterede accelerationer. Det er kendt, at Button bristede små blodkar under hans spins.
  8. hvilken procentdel af accelerationen på jordens overflade er accelerationen på grund af tyngdekraften ved positionen af en satellit placeret 300 km over jorden?
  9. Kontroller, at den lineære hastighed for en ultracentrifuge er omkring 0,50 km/s, og jorden i sin bane er omkring 30 km/s ved at beregne: (A) den lineære hastighed for et punkt på en ultracentrifuge 0.100 m fra centrum, roterende ved 50.000 omdr / min; (b) jordens lineære hastighed i sin bane omkring Solen (brug data fra teksten på radius af Jordens bane og tilnærm den som cirkulær).
  10. en roterende rumstation siges at skabe “kunstig tyngdekraft”—et løst defineret udtryk, der bruges til en acceleration, der groft ligner tyngdekraften. Den ydre væg på den roterende rumstation ville blive et gulv for astronauterne, og centripetal acceleration leveret af gulvet ville give astronauter mulighed for at udøve og opretholde muskel-og knoglestyrke mere naturligt end i ikke-roterende rummiljøer. Hvis rumstationen er 200 m i diameter, hvilken vinkelhastighed ville producere en “kunstig tyngdekraft” på 9,80 m/s2 ved fælgen?
  11. ved start har en kommerciel jet en hastighed på 60,0 m/s. Dens dæk har en diameter på 0,850 m. (A) ved hvor mange omdrejninger/min roterer dækkene? (b) Hvad er den centripetale acceleration ved dækkets kant? (c) med hvilken kraft skal en bestemt 1,00 liter 10-15 kg bakterie klamre sig til fælgen? (d) Tag forholdet mellem denne kraft og bakteriens vægt.
  12. integrerede koncepter. Ryttere i en forlystelsespark tur formet som et vikingeskib hængt fra en stor pivot drejes frem og tilbage som en stiv pendul. Engang nær midten af turen er skibet øjeblikkeligt ubevægeligt øverst på sin cirkelbue. Skibet svinger derefter ned under påvirkning af tyngdekraften. (a) hvis man antager ubetydelig friktion, skal man finde rytternes hastighed i bunden af dens bue i betragtning af systemets centrum for massebevægelser i en bue med en radius på 14,0 m, og Rytterne er tæt på massens centrum. (b) Hvad er den centripetale acceleration i bunden af buen? (C) Tegn et frit kropsdiagram over de kræfter, der virker på en rytter i bunden af buen. (d) Find den kraft, der udøves af turen på en 60,0 kg rytter, og sammenlign den med hendes vægt. (e) diskutere, om svaret synes rimeligt.
  13. urimelige resultater. En mor skubber sit barn på en sving, så hans hastighed er 9.00 m / s på det laveste punkt af hans vej. Gyngen er ophængt 2,00 m over barnets massecenter. (a) Hvad er størrelsen af barnets centripetale acceleration ved lavpunktet? (b) Hvad er størrelsen af den kraft, barnet udøver på sædet, hvis hans masse er 18,0 kg? (c) Hvad er urimeligt ved disse resultater? (D) hvilke præmisser er urimelige eller inkonsekvente?

ordliste

centripetal acceleration: accelerationen af et objekt, der bevæger sig i en cirkel, rettet mod midten

ultracentrifuge: en centrifuge optimeret til at dreje en rotor ved meget høje hastigheder

udvalgte løsninger på problemer & øvelser

1. 12, 9 omdr/min

3. 4 til 1021 m

5. (- en) 3,47 ren 104 m/s2, 3,55 ren 103 g; (b) 51,1 m/s

7. (a) 3.14 rad/s; (b) 118 m/s; (c)384 m/s; (d) den centripetale acceleration, som olympiske skatere føler, er 12 gange større end accelerationen på grund af tyngdekraften. Det er en hel del acceleration i sig selv. Den centripetale acceleration, der føltes af buttons næse, var 39,2 gange større end accelerationen på grund af tyngdekraften. Det er ikke underligt, at han sprængte små blodkar i sine spins.

9. (a) 0,524 km/s; (b) 29,7 km/S

11. (a) 1,35 liter 103 rpm; (b) 8,47 liter 103 m/s2; (c) 8,47 liter 10-12 N; (d) 865

12. (a) 16,6 m/s; (b) 19,6 m/s2;

(c)

et rektangel med en base længere end højden. En lodret linje med pilespidser i begge ender passerer gennem rektanglet og halverer de vandrette sider. Den øverste del af pilen er mærket N, og bunden er mærket V.;

(d) 1,76 til 103 N eller 3,00 V, det vil sige den normale kraft (opad) er tre gange hendes vægt; (E) dette svar virker rimeligt, da hun føler at hun bliver tvunget ind i stolen meget stærkere end bare ved tyngdekraften.

13. (a) 40,5 m/s2; (b) 905 N; (c) kraften i del (b) er meget stor. Accelerationen i del (A) er for meget, omkring 4 g; (d) svingets hastighed er for stor. Ved den givne hastighed i bunden af svingen er der nok kinetisk energi til at sende barnet hele vejen over toppen og ignorere friktion.