regressionsanalyse > Homoscedasticitet / homogenitet af varians / antagelse af lige varians

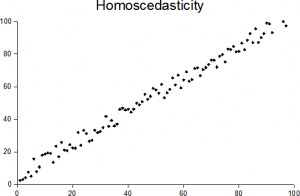
image: sreebot| Commons

enkelt sagt betyder homoscedasticity “at have den samme scatter.”For at det skal eksistere i et sæt data, skal punkterne være omtrent samme afstand fra linjen som vist på billedet ovenfor. Det modsatte er heteroscedasticitet (“forskellige scatter”), hvor punkter er i vidt forskellige afstande fra regressionslinjen.

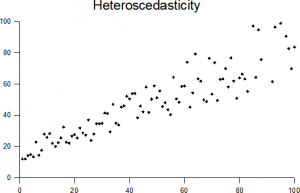
punkterne højere på h-aksen har en større varians end mindre værdier.

Bemærk, at jeg sagde “Afstand” her og ikke varians. Når du ser en graf, er det lettere at se på afstandene fra punkterne til linjen for at afgøre, om et datasæt viser homoscedasticitet. Teknisk set er det variansen, der tæller, og det er det, du vil bruge i beregninger. Da varians kræver en formel, er det imidlertid umuligt at øjeæble på en graf.

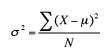
Variansformel.

da variansen kun er standardafvigelsen kvadreret, kan du også se homoscedasticitet beskrevet som en betingelse, hvor standardafvigelserne er ens for alle punkter.

i mere formelle termer

du kommer sjældent på tværs af et sæt data, der har en varians på nul. Det er mere sandsynligt, at du ser afvigelser, der spænder overalt fra 0,01 til 101,01. Så hvornår klassificeres et datasæt som homoscedasticity? Den generelle tommelfingerregel 1 er:

Hvis forholdet mellem den største varians og den mindste varians er 1,5 eller derunder, er dataene homoscedastic.

Hvad er antagelsen om lige varians?

antagelsen om lige afvigelser (dvs.antagelse af homoscedasticitet) antager, at forskellige prøver har den samme varians, selvom de kom fra forskellige populationer. Antagelsen findes i mange statistiske tests, herunder variansanalyse (ANOVA) og studerendes T-Test. Andre tests, som f.eks.
at køre en test uden at kontrollere for lige afvigelser kan have en betydelig indflydelse på dine resultater og kan endda ugyldiggøre dem fuldstændigt. Hvor meget dine resultater påvirkes afhænger af, hvilken test du bruger, og hvor følsom denne test er for ulige afvigelser. For eksempel, mens en ANOVA-test med fast faktor med lige prøvestørrelser kun påvirkes en lille mængde, kan en ANOVA med ulige prøvestørrelser give dig helt ugyldige resultater.

antagelsen om lige afvigelser anvendes også i lineær regression, som antager, at data er homoscedastic. Enkelt sagt, hvis dine data er bredt spredt om (som kegleform i det heteroscedastiske billede ovenfor), vil regression ikke fungere så godt. For mere om dette emne, se antagelser & betingelser for Regression.

test for homogenitet af varians

Test, som du kan køre for at kontrollere dine data opfylder denne antagelse, omfatter:

• Bartlett ‘s Test
• boks M Test
• brun-Forsythe Test
• Hartleys test
• Levene’ s Test

——————————————————————————

brug for hjælp til et hjemmearbejde eller test spørgsmål? Med Chegg Study kan du få trinvise løsninger på dine spørgsmål fra en ekspert på området. Dine første 30 minutter med en Chegg tutor er gratis!